maomao90's blog

Breaking the 100 point barrier for IOI 2010 Maze
By maomao90, history, 9 months ago, In English

After 21 days and 56 submissions on IOI 2010 Maze, I finally broke the 100 point barrier and achieved a score of 100.081 / 100.

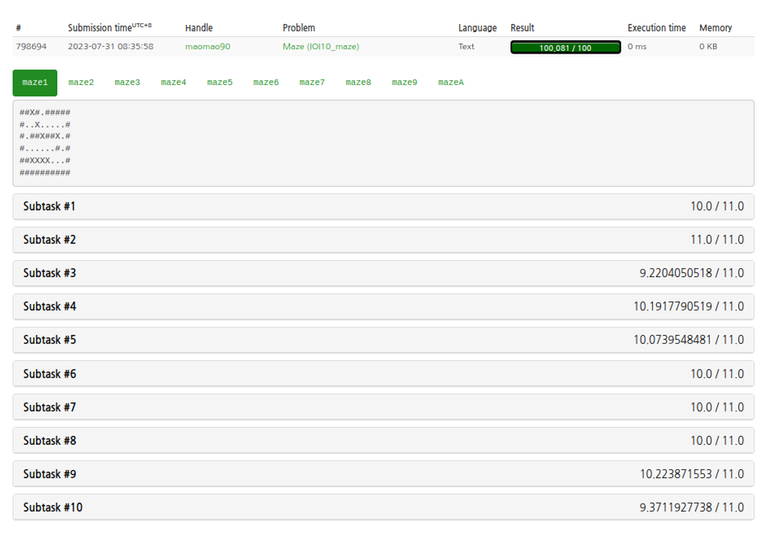
Score distribution Page 3 of submissions

Page 2 of submissions

Page 1 of submissions

Methodology

It's just simulated annealing + a lot a lot of time.

The neighbour function to generate a new state was just randomly choosing one cell to change from '$$$\text{#}$$$' to '$$$\text{.}$$$' or from '$$$\text{.}$$$' to '$$$\text{#}$$$'. Remember to take care that there must be exactly one '$$$\text{.}$$$' at the edge of the maze at all times.

The energy function that we are optimizing is the question itself, which is the maximum length of the shortest path.

The acceptance probability function is the classic exponential function based on the Boltzmann probability distribution.

Finally, the initial temperature used was $$$t_0 = 2.5$$$ with geometric temperature reduction $$$t' = t\cdot \alpha$$$ where $$$\alpha = 0.999999999$$$.

I did not do any optimisation for the energy function, So each iteration takes $$$O(RC)$$$, which is quite slow considering the extremely big $$$\alpha$$$ used. This is why I spent 21 days on this question as each run takes around 1 week to converge on the final answer 🤡.

Code

Takeaways

For such a brain-dead solution, I actually learnt quite a lot of things about simulated annealing. Below is a short list of items to take note of while doing simulated annealing.

  1. As the wise SGP IOI trainer bensonlzl told me: "Always write your intermediate solution to a file so that you can still get partial scores if it doesn't finish running before the contest ends". Writing to file can be quite time-consuming, so I only do it every ~1 million iterations.

  2. To choose a good $$$t_0$$$ and $$$\alpha$$$, I normally start with a high $$$t_0$$$ and a low $$$\alpha$$$, then print the temperature and the energy function after each iteration. Then, I try to choose a $$$t_0$$$ where the energy is not completely random but at the same time there are significant jumps in energy to ensure that enough exploration takes place. I binary search on the $$$\alpha$$$ to use based on how slowly the temperature decreases over time and try to pick the one that is neither too slow nor too fast.

  3. Most of the time running the simulated annealing for a longer time with bigger $$$\alpha$$$ is better than trying to improve a previous solution by letting the initial state be the previous solution and starting with a lower $$$t_0$$$. This is probably because the latter has a higher chance to be stuck in a local minimum.

  4. In a real 5-hour contest scenario, do not spend too much time on the output-only problem. Spend a short time coding the simulated annealing and work on the remaining problems while the code is running in the background. Do not be like me and spend the majority of the contest trying to increase my score from ~80 to ~90 and end up having low score on other problems.

Special Thanks

Of course, this could not have been done without the help of the following people:

  1. bensonlzl, the SGP IOI trainer, for teaching me simulated annealing and including this problem in one of the training contest.

  2. rainboy for giving me the motivation to get higher than him as he was the first place before I beat him.

  3. jamessngg for helping me to solve test case 8 by hand and buying purple candy for the SGP IOI team.

  4. pavement for giving moral support and suggestions as part of the SGP IOI team.

  5. NUS for supplying electricity so that I can keep the NUS computer on for 3 consecutive weeks while running the simulated annealing.

Multiple terminals running simulated annealing

Conclusion

Feel free to try to beat my score or tell me about any possible optimizations in the comments.

  • Vote: I like it
  • +310
  • Vote: I do not like it

»
9 months ago, # |
  Vote: I like it +7 Vote: I do not like it

orz

(I am familiar with the recent blogs and stuff but I couldn't bare it lol)

→ Reply
»
9 months ago, # |
  Vote: I like it +1 Vote: I do not like it

wtf this is wild

→ Reply
»
9 months ago, # |
  Vote: I like it 0 Vote: I do not like it

You must be Chuck Norris

→ Reply
»
9 months ago, # |
← Rev. 2   Vote: I like it +217 Vote: I do not like it

Headlines of similar feel:

  1. 358 years after its formulation, a mathematician proved Fermat Last Theorem, costing years of research.
  2. 36 years after its release, a speedrunner finished Super Mario Bros faster than 4 minute 55 seconds, costing countless hours of attempts.
  3. 13 years after IOI 2010, a competitive programmer broke the 100 point barrier for Maze, costing 3 consecutive weeks of NUS computational power.
→ Reply
»
9 months ago, # |
  Vote: I like it 0 Vote: I do not like it

🤯

→ Reply
»
9 months ago, # |
  Vote: I like it 0 Vote: I do not like it

If you were in IOI 2010, you might be the first to get >600 pointssss xd

→ Reply
  • »
    »
    9 months ago, # ^ |
      Vote: I like it +47 Vote: I do not like it

    If IOI 2010 was three weeks long maybe

    → Reply
  • »
    »
    9 months ago, # ^ |
      Vote: I like it +58 Vote: I do not like it

    Also, Tourist got 778 points at IOI 2010, he is that good IOI 2010 was the last IOI (to date) to have 8 tasks.

    → Reply
»
9 months ago, # |
  Vote: I like it 0 Vote: I do not like it

Unusual problem. By some reason, the max score is 110 https://stats.ioinformatics.org/tasks/2010/maze

→ Reply
»
9 months ago, # |
← Rev. 2   Vote: I like it 0 Vote: I do not like it

Is it possible to recalculate the score function after the change in O((R + C) log (R+C)), or even in O(R + C)? that would improve efficiency by a lot. But probably using different score function, that better fits simulated annealing and is easier to optimize, is better.

Also, I ran my own simulated annealing overnight and it found a better solution to the 9th test, other runs got corrupted smh and the output was gibberish :,(

https://oj.uz/submission/805436
code: https://pastebin.com/0iFixk2p

→ Reply
  • »
    »
    9 months ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    Hmm do you have a suggestion for the different score function?

    Thanks for telling me that there is a better solution for the 9th test. I thought that it was already the optimal, so I stopped running the simulated annealing for the 9th test. Maybe I'll try to rerun it to see whether I can get a better result.

    → Reply