Tutorial
Tutorial is loading...
Code
#include <bits/stdc++.h>
using namespace std;
const int sz = 1e5 + 10;
int ara[sz];
int main()
{
int t;
scanf("%d", &t);
while(t--) {
int n;
scanf("%d", &n);
int sum = 0;
for(int i = 1; i <= n; i++) {
scanf("%d", &ara[i]);
sum += ara[i];
}
int ans = -1e9;
for(int i = 1; i < n; i++) {
if(ara[i] == ara[i+1]) {
if(ara[i] == 1) ans = max(ans, sum-4);
else ans = max(ans, sum+4);
}
else
ans = max(ans, sum);
}
printf("%d\n", ans);
}
return 0;
}
1778B - The Forbidden Permutation
Tutorial
Tutorial is loading...
Code
#include <bits/stdc++.h>
using namespace std;
const int sz = 1e5+10;
int p[sz], a[sz], pos[sz];
int main()
{
int t;
scanf("%d", &t);
while(t--) {
int n, m, d;
scanf("%d %d %d", &n, &m, &d);
for(int i = 1; i <= n; i++) {
scanf("%d", &p[i]);
pos[ p[i] ] = i;
}
for(int i = 1; i <= m; i++) {
scanf("%d", &a[i]);
}
int ans = 1e9;
for(int i = 1; i < m; i++) {
if(pos[a[i+1]] <= pos[a[i]] || pos[a[i+1]]-pos[a[i]] > d) {
ans = 0;
break;
}
ans = min(ans, pos[a[i+1]] - pos[a[i]]);
int dist = pos[a[i+1]]-pos[a[i]];
int swapNeed = d-dist+1;
int swapPossible = (pos[a[i]]-1) + (n - pos[a[i+1]]);
if(swapPossible >= swapNeed) ans = min(ans, swapNeed);
}
printf("%d\n", ans);
}
return 0;
}
Tutorial
Tutorial is loading...
Code
#include <bits/stdc++.h>
using namespace std;
#define ll long long
#define pb push_back
#define EL '\n'
#define fastio std::ios_base::sync_with_stdio(false);cin.tie(NULL);cout.tie(NULL);
string a, b;
string char_list;
bool mark[26];
ll ans, k;
ll count_matching_pair()
{
ll tot_pair = 0, match_count = 0;
for(ll i = 0; i < a.size(); i++) {
if(a[i] == b[i] || mark[ a[i]-'a' ])
match_count++;
else {
tot_pair += match_count*(match_count+1)/2;
match_count = 0;
}
}
tot_pair += match_count*(match_count+1)/2;
return tot_pair;
}
void solve(ll pos, ll cnt)
{
if(cnt > k) return;
if(pos == char_list.size()) {
if(cnt == k) ans = max(ans, count_matching_pair());
return;
}
solve(pos+1, cnt);
mark[ char_list[pos]-'a' ] = 1;
solve(pos+1, cnt+1);
mark[ char_list[pos]-'a' ] = 0;
}
int main()
{
fastio;
ll t;
cin >> t;
while(t--) {
ll n; cin >> n >> k;
cin >> a >> b;
unordered_set <char> unq;
for(auto &ch : a) unq.insert(ch);
char_list.clear();
for(auto &x : unq) char_list.pb(x);
k = min(k, (ll)unq.size());
memset(mark, 0, sizeof mark);
ans = 0;
solve(0, 0);
cout << ans << EL;
}
return 0;
}
1778D - Flexible String Revisit
Tutorial$$$ \begin{align} f(x) = \frac{x}{n} \cdot [1 + f(x-1)] + \frac{n-x}{n} \cdot [1 + f(x+1)]\\ or,~~~ f(x) = 1 + \frac{x}{n}\cdot f(x-1) + \frac{n-x}{n} \cdot f(x+1) \end{align} $$$
1778D - Flexible String Revisit
Let $$$k$$$ be the number of indices where the characters between two strings are different and $$$f(x)$$$ be the expected number of moves to make two strings equal given that the strings have $$$x$$$ differences. We have to find the value of $$$f(k)$$$.
For all $$$x$$$ where $$$1 \leq x \leq n-1$$$,
Now, $$$f(0) = 0$$$ and $$$f(1) = 1 + \frac{n-1}{n}f(2)$$$.
We can represent any $$$f(i)$$$ in the form $$$f(i) = a_i + b_i \cdot f(i+1)$$$.
Let, $$$a_{1} = 1$$$ and $$$b_{1} = \frac{n-1}{n}$$$. So, we can write $$$f(1) = a_{1} + b_{1}\cdot f(2)$$$.
When $$$1 \lt i \lt n$$$, $$$f(i) = 1 + \frac{i}{n} \cdot f(i-1) + \frac{n-i}{n} \cdot f(i+1)$$$. We can substitute the value of $$$f(i-1)$$$ with $$$a_{i-1} + b_{i-1}\cdot f(i)$$$ and calculate the value of $$$f(i)$$$. Thus we can get the value of $$$a_i$$$ and $$$b_i$$$ using the value of $$$a_{i-1}$$$ and $$$b_{i-1}$$$ by considering $$$a_1$$$ and $$$b_1$$$ as the base case.
We get, $$$a_{i} = \frac{n+i\cdot a_{i-1}}{n-i\cdot b_{i-1}}$$$ and $$$b_{i} = \frac{n-i}{n-i \cdot b_{i-1}}$$$ for $$$2 \leq i \leq n$$$.
Calculation$$$ \begin{align} f(i) & = 1 + \frac{i}{n} \cdot [a_{i-1} + b_{i-1}\cdot f(i)] + \frac{n-i}{n} \cdot f(i+1)\\ & = 1 + \frac{i}{n}\cdot a_{i-1} + \frac{i}{n} \cdot b_{i-1} \cdot f(i) + \frac{n-i}{n} \cdot f(i+1)\\ & = \frac{1+\frac{i}{n}\cdot a_{i-1}}{1-\frac{i}{n}\cdot b_{i-1}} + \frac{n-i}{n-i \cdot b_{i-1}}f(i+1)\\ & = \frac{n+i\cdot a_{i-1}}{n-i\cdot b_{i-1}} + \frac{n-i}{n-i \cdot b_{i-1}}f(i+1)\\ & = a_{i} + b_{i} \cdot f(i+1) \end{align} $$$
Substituting $$$f(i-1) = a_{i-1} + b_{i-1}\cdot f(i)$$$,
So, $$$a_{i} = \frac{n+i\cdot a_{i-1}}{n-i\cdot b_{i-1}}$$$ and $$$b_{i} = \frac{n-i}{n-i \cdot b_{i-1}}$$$ for $$$2 \leq i \leq n$$$.
Similarly, $$$f(n) = 1+f(n-1)$$$.
We can represent any $$$f(i)$$$ in the form $$$f(i) = c_i + d_i \cdot f(i-1)$$$.
Let, $$$c_{n} = 1$$$ and $$$d_{n} = 1$$$. So, we can write $$$f(n) = c_{n} + d_{n}\cdot f(n-1)$$$.
When $$$1 \lt i \lt n$$$, $$$f(i) = 1 + \frac{i}{n} \cdot f(i-1) + \frac{n-i}{n} \cdot f(i+1)$$$. We can substitute the value of $$$f(i+1)$$$ with $$$c_{i+1} + d_{i+1}\cdot f(i)$$$ and calculate the value of $$$f(i)$$$. Thus we can get the value of $$$c_i$$$ and $$$d_i$$$ using the value of $$$c_{i+1}$$$ and $$$d_{i+1}$$$ by considering $$$c_n$$$ and $$$d_n$$$ as the base case.
We get, $$$c_{i} = \frac{n+(n-i)\cdot c_{i+1}}{n-(n-i)\cdot d_{i+1}}$$$ and $$$d_{i} = \frac{i}{n-(n-i) \cdot d_{i+1}}$$$.
Calculation$$$ \begin{align} f(i) & = 1 + \frac{i}{n} \cdot f(i-1) + \frac{n-i}{n} \cdot [c_{i+1} + d_{i+1}\cdot f(i)]\\ & = 1 + \frac{i}{n}\cdot f(i-1) + \frac{n-i}{n} \cdot c_{i+1} + \frac{n-i}{n} \cdot d_{i+1} \cdot f(i)\\ & = \frac{1+\frac{n-i}{n}\cdot c_{i+1}}{1-\frac{n-i}{n}\cdot d_{i+1}} + \frac{i}{n-(n-i) \cdot d_{i+1}}f(i-1)\\ & = \frac{n+(n-i)\cdot c_{i+1}}{n-(n-i)\cdot d_{i+1}} + \frac{i}{n-(n-i) \cdot d_{i+1}}f(i-1)\\ & = c_{i} + d_{i} \cdot f(i-1) \end{align} $$$
Substituting $$$f(i+1) = c_{i+1} + d_{i+1}\cdot f(i)$$$,
So, $$$c_{i} = \frac{n+(n-i)\cdot c_{i+1}}{n-(n-i)\cdot d_{i+1}}$$$ and $$$d_{i} = \frac{i}{n-(n-i) \cdot d_{i+1}}$$$.
Now, $$$f(i) = c_i + d_i \cdot f(i-1)$$$ and $$$f(i-1) = a_{i-1} + b_{i-1} \cdot f(i)$$$. By solving these two equations, we find that $$$f(i) = \frac{c_i+d_i \cdot a_{i-1}}{1-d_i \cdot b_{i-1}}$$$.
Time Complexity: $$$\mathcal{O}(n\cdot \log m)$$$.
Alternative Solution
After some calculations, it can be shown that $$$f(1) = 2^n - 1$$$. Now we know $$$f(0) = 0$$$ and $$$f(1) = 2^n - 1$$$.
From the relation between $$$f(i)$$$, $$$f(i-1)$$$ and $$$f(i-2)$$$, we can write $$$f(i) = \frac{n\cdot f(i-1) - i \cdot f(i-2) - n}{n-i+1}$$$.
Code
#include <bits/stdc++.h>
using namespace std;
#define mod 998244353
#define N 1000005
template<int MOD>
struct ModInt {
unsigned x;
ModInt() : x(0) { }
ModInt(signed sig) : x(sig) { }
ModInt(signed long long sig) : x(sig%MOD) { }
int get() const { return (int)x; }
ModInt pow(ll p) { ModInt res = 1, a = *this; while (p) { if (p & 1) res *= a; a *= a; p >>= 1; } return res; }
ModInt &operator+=(ModInt that) { if ((x += that.x) >= MOD) x -= MOD; return *this; }
ModInt &operator-=(ModInt that) { if ((x += MOD - that.x) >= MOD) x -= MOD; return *this; }
ModInt &operator*=(ModInt that) { x = (unsigned long long)x * that.x % MOD; return *this; }
ModInt &operator/=(ModInt that) { return (*this) *= that.pow(MOD - 2); }
ModInt operator+(ModInt that) const { return ModInt(*this) += that; }
ModInt operator-(ModInt that) const { return ModInt(*this) -= that; }
ModInt operator*(ModInt that) const { return ModInt(*this) *= that; }
ModInt operator/(ModInt that) const { return ModInt(*this) /= that; }
bool operator<(ModInt that) const { return x < that.x; }
friend ostream& operator<<(ostream &os, ModInt a) { os << a.x; return os; }
};
typedef ModInt<998244353> mint;
mint a[N], b[N], c[N], d[N];
int main(){
ios::sync_with_stdio(false);
cin.tie(0);
int t;
cin >> t;
while(t--){
int n;
cin >> n;
string s1, s2;
cin >> s1 >> s2;
int diff = 0;
for(int i = 0; i < n; i++){
diff += s1[i]!=s2[i];
}
c[n] = 1, d[n] = 1, a[1] = 1, b[1] = ((mint) n-1)/n;
for(int i = 2; i <= n; i++){
a[i] = ((mint) n + a[i-1]*i)/((mint) n - b[i-1]*i);
b[i] = ((mint) n-i)/((mint) n - b[i-1]*i);
}
for(int i = n-1; i >= 1; i--){
c[i] = ((mint) n + c[i+1]*(n-i))/((mint) n - d[i+1]*(n-i));
d[i] = (mint) i / ((mint) n - d[i+1]*(n-i));
}
mint ans = (c[diff]+d[diff]*a[diff-1])/((mint) 1 - d[diff]*b[diff-1]);
cout << ans << endl;
}
return 0;
}
Alternative Code
#include <bits/stdc++.h>
using namespace std;
#define ll long long
template<int MOD>
struct ModInt {
unsigned x;
ModInt() : x(0) { }
ModInt(signed sig) : x(sig) { }
ModInt(signed long long sig) : x(sig%MOD) { }
int get() const { return (int)x; }
ModInt pow(ll p) { ModInt res = 1, a = *this; while (p) { if (p & 1) res *= a; a *= a; p >>= 1; } return res; }
ModInt &operator+=(ModInt that) { if ((x += that.x) >= MOD) x -= MOD; return *this; }
ModInt &operator-=(ModInt that) { if ((x += MOD - that.x) >= MOD) x -= MOD; return *this; }
ModInt &operator*=(ModInt that) { x = (unsigned long long)x * that.x % MOD; return *this; }
ModInt &operator/=(ModInt that) { return (*this) *= that.pow(MOD - 2); }
ModInt operator+(ModInt that) const { return ModInt(*this) += that; }
ModInt operator-(ModInt that) const { return ModInt(*this) -= that; }
ModInt operator*(ModInt that) const { return ModInt(*this) *= that; }
ModInt operator/(ModInt that) const { return ModInt(*this) /= that; }
bool operator<(ModInt that) const { return x < that.x; }
friend ostream& operator<<(ostream &os, ModInt a) { os << a.x; return os; }
};
typedef ModInt<998244353> mint;
int main(){
ios::sync_with_stdio(false);
cin.tie(0);
cout.tie(0);
mint two = 2;
int t;
cin >> t;
while(t--){
int n;
cin >> n;
string a, b;
cin >> a >> b;
int cnt = 0;
for(int i = 0; i < n; i++){
if(a[i]!=b[i]) cnt++;
}
vector<mint> dp(n+2);
dp[0] = two.pow(n);
dp[1] = dp[0]-1;
dp[0] = 0;
for(long long i = 2; i < n; i++){
mint x = i-1;
x /= n;
dp[i] = (dp[i-1]-x*dp[i-2]-1)*n/(n-i+1);
}
dp[n] = dp[n-1]+1;
cout << dp[cnt] << '\n';
}
return 0;
}
Tutorial
Tutorial is loading...
Code
#include <bits/stdc++.h>
using namespace std;
#define ll long long
#define pb push_back
#define nn '\n'
#define fastio std::ios_base::sync_with_stdio(false); cin.tie(NULL);
const int sz = 2e5 + 10, d = 30;
vector <int> g[sz], Tree[sz];
int a[sz], discover_time[sz], finish_time[sz], nodeOf[sz], tim;
struct BASIS {
int basis[d];
int sz;
void init() {
for(int i = 0; i < d; i++) basis[i] = 0;
sz = 0;
}
void insertVector(int mask) {
for (int i = d-1; i >= 0; i--) {
if (((mask>>i)&1) == 0) continue;
if (!basis[i]) {
basis[i] = mask;
++sz;
return;
}
mask ^= basis[i];
}
}
void mergeBasis(const BASIS &from) {
for(int i = d-1; i >= 0; i--) {
if(!from.basis[i])
continue;
insertVector(from.basis[i]);
}
}
int findMax() {
int ret = 0;
for(int i = d-1; i >= 0; i--) {
if(!basis[i] || (ret>>i & 1))
continue;
ret ^= basis[i];
}
return ret;
}
} in[sz], out, pre[sz], suf[sz];
void in_dfs(int u, int p)
{
in[u].insertVector(a[u]);
discover_time[u] = ++tim;
nodeOf[tim] = u;
for(auto &v : g[u]) {
if(v == p)
continue;
Tree[u].pb(v);
in_dfs(v, u);
in[u].mergeBasis(in[v]);
}
finish_time[u] = tim;
}
inline bool in_subtree(int sub_root, int v)
{
return discover_time[sub_root] <= discover_time[v]
&& finish_time[sub_root] >= finish_time[v];
}
int findChildOnPath(int sub_root, int v)
{
int lo = 0, hi = (int)Tree[sub_root].size()-1;
while(lo <= hi) {
int mid = lo+hi>>1, node = Tree[sub_root][mid];
if(finish_time[node] < discover_time[v])
lo = mid + 1;
else if(discover_time[node] > discover_time[v])
hi= mid - 1;
else
return node;
}
}
void init(int n) {
for(int i = 0; i <= n+5; i++) {
g[i].clear(), Tree[i].clear();
in[i].init();
pre[i].init(), suf[i].init();
}
tim = 0;
}
int main()
{
fastio;
int t;
cin >> t;
while(t--) {
int n; cin >> n;
init(n);
for(int i = 1; i <= n; i++) cin >> a[i];
for(int i = 1; i < n; i++) {
int u, v;
cin >> u >> v;
g[u].pb(v); g[v].pb(u);
}
in_dfs(1, -1);
for(int i = 1; i <= n; i++) {
pre[i].insertVector(a[ nodeOf[i] ]);
pre[i].mergeBasis(pre[i-1]);
}
for(int i = n; i >= 1; i--) {
suf[i].insertVector(a[ nodeOf[i] ]);
suf[i].mergeBasis(suf[i+1]);
}
int q; cin >> q;
while(q--) {
int root, v;
cin >> root >> v;
if(root == v) {
cout << in[1].findMax() << nn;
}
else if(in_subtree(v, root)) {
int child = findChildOnPath(v, root);
out.init();
out.mergeBasis(pre[discover_time[child]-1]);
out.mergeBasis(suf[finish_time[child]+1]);
cout << out.findMax() << nn;
}
else
cout << in[v].findMax() << nn;
}
}
return 0;
}
Tutorial
Tutorial is loading...
Code
#include <bits/stdc++.h>
using namespace std;
const int N = 100005;
const int mod = 998244353;
int val[N];
vector<int> g[N];
vector<int> divisor[N];
int subtree_gcd[N], par[N];
int dp[N][1003];
int gcdd[1003][1003];
inline long long ___gcd(long long a, long long b){
if(gcdd[a][b]) return gcdd[a][b];
return gcdd[a][b] = __gcd(a, b);
}
inline long long lcm(long long a, long long b){
return (a/___gcd(a, b))*b;
}
void dfs(int u, int p){
par[u] = p;
subtree_gcd[u] = val[u];
for(int v: g[u]){
if(v==p) continue;
dfs(v, u);
subtree_gcd[u] = ___gcd(subtree_gcd[u], subtree_gcd[v]);
}
}
int solve(int u, int d, int p){
if(subtree_gcd[u]%d==0) return 0;
if((val[u]*val[u])%d) return (1<<30);
if(dp[u][d]!=-1) return dp[u][d];
long long req = d/___gcd(d, subtree_gcd[u]);
long long res = (1<<30);
for(int div: divisor[val[u]]){
if((val[u]*div)%d==0 && d%div==0){
long long r = 1;
for(int v: g[u]){
if(v==p) continue;
r += solve(v, lcm(d/div, div), u);
}
res = min(res, r);
}
}
return dp[u][d] = min(res, (1LL<<30));
}
int main(){
ios::sync_with_stdio(false);
cin.tie(nullptr);
for(int i = 2; i < 1001; i++){
for(int j = i; j < 1001; j+=i){
divisor[j].push_back(i);
}
}
int t;
cin >> t;
while(t--){
int n, k;
cin >> n >> k;
for(int i = 0; i <= n; i++){
g[i].clear();
}
for(int i = 1; i <= n; i++){
cin >> val[i];
}
for(int i = 0; i <= n; i++){
for(int d: divisor[val[1]]){
dp[i][d] = -1;
}
}
for(int i = 0; i < n-1; i++){
int u, v;
cin >> u >> v;
g[u].push_back(v);
g[v].push_back(u);
}
dfs(1, 0);
int ans = val[1];
for(int d: divisor[val[1]]){
int req = 0;
int f = 1;
for(int v: g[1]){
int x = solve(v, d, par[v]);
if(x>n) f = 0;
req += x;
}
if(!f) continue;
req++;
if(req<=k){
ans = max(ans, val[1]*d);
}
}
cout << ans << "\n";
}
return 0;
}
Better round than I expected, kudos to the authors!
I agree, the authors are cool!
Special thanks to Psychotic_D for the special case of problem D.
What was the special case?
Test case 24 of problem D where the answer is mod-1. A lot of solutions failed in the system test in this case.
Wow! Big brain. It was really so great. Orzzz Psychotic_D !
In problem b why we are not updating the position of the element after we have counted the number of swaps. how this is not affecting the ans?
Maybe because there is no need to update. As we only need the number of minimum swaps/steps required to make array good.
Seems like you misunderstood the problem just like me. Actually, we just need to change one such pair that satisfies the given inequality to make the array good. I feel so stupid now and was wondering why is B so difficult and how are people solving it.
negation(for all)= there exits. i too could not see that.
Let me read the question once again. I too could not see that. Guess we need to use light pen to see it
me too, I did the harder version of the problem ie to make the complete array good in minimum moves XD
But what if the question was originally what you thought it was... that you need to make all pairs good in the array? Would that be dp?
I can't figure out how to solve that question by dp,since previous moves may affect these rear one. That's why I don't solve the problem LOL
me too
me too
me too.I will be sad all day.
damn damn damn damn same thing happened to me and I just realized now. I tried to solve the problem for a whole day yesterday and rolled in guilt why I cant get a B problem now that I know I misunderstood the problem after reading this comment.
lol same
Me too.
$$$pos(a_i)<pos(a_{i+1})≤pos(a_i)+d$$$ for all $$$1≤i<m$$$.
I'm so foolish and careless.
I got stuck at B because I didn't read the question correctly learned a big lesson thank s for the contest.
Me too. I tried to make the whole array good that's why i found this problem so difficult
Same for me, I did't realise that only one pair was enough for the answer.
same for me, I understand proper question after 30 minutes.
Anyone care to explain the "After some calculations" part of the Alternative solution for D? I'd really like to see the idea behind this :)
One possible way to show this is using Markov chains (you might want to look up Ehrenfest Urns)
In particular, suppose that we don't stop after having $$$0$$$ differences between $$$a$$$ and $$$b$$$: instead, we keep repeating the index choosing infinitely. Then, the probability of being in state $$$0$$$ differences in the long run is $$$\pi_0 = 2^{-n}$$$. It is a fact of "recurrent" Markov chains that the expected time to return to a state $$$i$$$ is $$$1/\pi_i$$$. In particular, if currently there are $$$0$$$ differences between the two strings, then the expected time until we return back to having $$$0$$$ differences is $$$2^n$$$ moves. However, note that when we leave $$$0$$$ differences, we always move to $$$1$$$ difference. So, the expected time to go from $$$1$$$ difference to $$$0$$$ differences must be $$$2^n - 1$$$.
This is so cool! Thank you so much.
Cool
Could u tell me how why the probability is 2^(-n)?
Suppose you have a long run probability $$$\pi_i$$$ of being in state $$$i$$$ and probability $$$\pi_{i+1}$$$ of being in state $$$i + 1$$$. Then, notice that the number of times you go $$$i\rightarrow i + 1$$$ is within one of the number of times you go $$$i + 1\rightarrow i$$$. In the limit, this means that of the $$$i\rightarrow i + 1$$$ and $$$i + 1\rightarrow i$$$ transitions, exactly $$$\frac 12$$$ of them are $$$i\rightarrow i + 1$$$.
Since the probability of going from $$$i$$$ to $$$i + 1$$$ is $$$\frac{n - i}{n}$$$ and the probability of going from $$$i + 1$$$ to $$$i$$$ is $$$\frac{i + 1}{n}$$$, it follows that
Rearranging, you have $$$\pi_{i+1} = \pi_i \cdot \frac{n - i}{i + 1}$$$. Then, by induction you can verify that this implies that $$$\pi_{i+1} = \pi_0 \cdot \binom {n}{i + 1}$$$.
Since $$$\sum_{i=0}^{n}\pi_i = 1$$$, adding these up implies that $$$\sum_{i=0}^{n}\pi_0 \cdot \binom ni = 1$$$. Since $$$\sum_{i=0}^{n}\binom ni = 2^n$$$, this gives $$$\pi_0 = 2^{-n}$$$.
Dude, that was soooo beautiful!! Thanks a lot!! Could u suggest which topics I should study to be able to do these on my own? Thanks a lot in advance.
Here's another simple way to show the stationary probability is $$$\frac{1}{2^n}$$$ more simply. We are taking a random walk on the vertices of the boolean hypercube with vertices $$$\{0,1\}^n.$$$ (Each of the $$$n$$$ bits corresponds to one dimension of the cube), and toggling one bit corresponds to moving along an edge. This is clearly symmetric with respect to each of the $$$2^n$$$ vertices. By symmetry of the cube, the stationary probability is the same for each vertex and so each is equal to $$$\frac{1}{2^n}.$$$
More generally the stationary distribution on an unweighted finite graph (neighbors picked uniformly at random) is $$$\pi_v = \frac{deg(v)}{2E}$$$ where $$$E$$$ is the number of edges.
I had the same solution as mentioned in the editorial for question B but i got wrong answer on pretest 2.
Me too
I would like to point out that there is a much easier way for D. You can find through some checking that if A and B differ in exactly 1 bit, then the expected value is 2^n-1. Then you can just create an array and calculate the answer recursively, using some Modulo properties which make it much easier.
An implementation can be found here. Ignore the copy-pasted GeeksforGeeks implementation of Modular Inverse :clown:
Elaborate the relation of ans[i] please !! unable to understand completely.
Another solution for D: let $$$f(i)$$$ be the expected time to go from $$$i$$$ differences to $$$i - 1$$$ differences for the first time. Then, our answer is $$$\sum_{i=1}^{k} f(i)$$$.
The claim is that $$$f(i) = 1 + \frac{n-i}{n}(f(i + 1) + f(i))$$$. Indeed, with probability $$$\frac in$$$ , we move to $$$i - 1$$$ differences and are done in one move. Else, we move to $$$i + 1$$$ differences. Then, the expected time to get to $$$i - 1$$$ is $$$f(i + 1) + f(i)$$$.
So, we can rearrange to get $$$f(i) = \frac ni + \frac{n-i}i f(i + 1)$$$. Now, in $$$O(n)$$$ we can calculate all $$$f(i)$$$ starting from $$$n$$$ and ending at $$$1$$$, and $$$O(n)$$$ to compute the desired sum.
Submission: 191566655
Wow, nice solution
Cool.
amazing！
I've also used this method to solve D. I'd like to add some explanations in order to give others a further understanding.
We can know that if we are considering $$$f(i)$$$, we could move to $$$i - 1$$$ by $$$1$$$ step with probability $$$\dfrac{i}{n}$$$, or we could move to $$$i + 1$$$ by $$$1$$$ step then move to $$$i - 1$$$ by step $$$f(i) + f(i - 1)$$$ with probability $$$\dfrac{n - i}{n}$$$.
So we can find that $$$f(i) = \dfrac{i}{n} \times 1 + \dfrac{n - i}{n} \times (f(i) + f(i + 1) + 1) \iff f(i) = 1 + \dfrac{n - i}{n}(f(i) + f(i + 1))$$$ like what applepi216 said.
It is OK if we have $$$f(i)$$$ on both sides of the equal sign, we just have to move all $$$f(i)$$$ to the same side like: $$$f(i) = 1 + \dfrac{n - i}{n}(f(i) + f(i + 1))\iff \dfrac{i}{n}f(i) = 1 + \dfrac{n - i}{n}f(i + 1) \iff f(i) = \dfrac{n}{i} + \dfrac{n - i}{i}f(i + 1)$$$
Then we can easily write a program to solve this problem!
This formula can be explained in another way.
Assume we have $$$\displaystyle i$$$ one's. The probability of that number decreasing is exactly $$$\displaystyle \frac{i}{n}$$$. That means that it will decrease on the $$$\displaystyle \frac{n}{i}$$$-s attempt on average. Therefore, we claim that we expect $$$\displaystyle \frac{n}{i} - 1$$$ increases and exactly $$$\displaystyle 1$$$ decrease.
So, we get that $$$\displaystyle dp_i = (\frac{n}{i} - 1) * (dp_{i+1} + 1) + 1$$$, because we have to waste one extra move for each increase.
Thank you so much
I have an easier solution for E without using Euler tour. I use re-rooting technique and answer the queries offline. Submission here.
In problem B i think i should fix all i and don't solve the problem at the end ಥ‿ಥ
same here bro
To find the node $$$c$$$, one can also use binary lifting/k-th ancestor techniques. The relevant node will be the $$$dep[r] - dep[v] - 1$$$'th ancestor of $$$r$$$.
Can anyone tell me where am I wrong here? Getting wrong answer on the last input of the first test case.
ll n,m,d,i,ans1,ans2,mini=INT_MAX,cnt=0; cin>>n>>m>>d; unordered_map<ll,ll> p; ll a[m],b[n]; for(i=1;i<=n;i++){ cin>>b[i]; p.insert({b[i],i});} for(i=1;i<=m;i++) cin>>a[i];
for ( i = 1; i < m; i++){ if(p[a[i]] > p[a[i+1]] || p[a[i]]+d < p[a[i+1]]){ cout<<0<<endl; cnt=0; break; } else{ ans1 = abs(p[a[i]] — p[a[i+1]]); ans2 = abs((p[a[i]] + d) — p[a[i+1]]) + 1; if((p[a[i]] + d) >= n){ ans2=INT_MAX; } if(ans1<ans2) mini = min(mini,ans1); else mini = min(mini,ans2); cnt++; } } if(cnt>0) cout<<mini<<endl;
You're not supposed to paste your code in discussion.
In problem B, do we need to check if the array has become good after every swap?
you dont need to swap anything in the original array. Just need to calculate how many swaps are required per pair. The minimum of all pairs is the answer (something similar is written in the solution)
yes, we only need only one index which does not follow the condition of not good array. So after swapping an element we check minimum numbers of swaps for every time.
Yes. Because if all inequalities are satisfied, sequence a is a bad sequence.
For problem D, it is pretty intuitive that the answer only depends on the count of positions with different characters in the two strings, but can someone show me how to prove this formally/mathematically?
Suppose $$$a$$$ is different from $$$b$$$ at $$$k$$$ places. First notice that it only matters if $$$a_i = b_i$$$ or $$$a_i \neq b_i$$$, and not what the exact values are. That means that we if we flip both $$$a_i$$$ and $$$b_i$$$ the answer won't change. So we can assume that $$$b$$$ consists only of zeros, and $$$a$$$ has exactly $$$k$$$ ones. Now, if $$$X$$$ is uniformly distributed, then so is $$$p(X)$$$, where $$$p$$$ is some permutation of $$$1...n$$$. That means that if we permute $$$a$$$ and $$$b$$$ in the same way the answer won't change. So we can assume that $$$a = 0...01...1$$$ with $$$k$$$ ones and $$$b = 0...0$$$. Since all tests with the same $$$k$$$ can be transformed into the same "canonical" form without changing the answer, they all share the same answer.
Can someone help prove that using sliding window greedily is incorrect for problem C ? I tried to use this idea but got WA. My submission is 191628511
The idea I tried to implement is that we keep a running map that reflects the unique letters of set Q. Whenever the Q's size is < k or a letter has already existed in Q, we can safely make a[i] == b[i], in case they are different.
Here is an another calculation for D:
we have $$$f(n-1) = 1 + \frac{n-1}{n}f(n-2)+\frac{1}{n}f(n)$$$ and $$$f(n) = 1 + f(n-1)$$$ ,
then get $$$f(n-1) = f(n-2) + \frac{n+1}{n-1} $$$.
Noted that the second part is only related to $$$i$$$, so we can caculate this part for every $$$i$$$ from $$$n-1$$$ to $$$1$$$, with $$$f(0) = 0$$$, all $$$f(i)$$$ can be calculated.
My submission: https://codeforces.com/contest/1778/submission/191601709
There were better ways of explaining question B but bro wake up and choose violence.
B taught me to read problems properly T.T
Seems like I'm not the only one who got brainfucked in B, thinking we have to make all the pairs good :)
Nice contest tho!
Geothermal can you please explain your solution to D ?
Let $$$x_m$$$ be the expected number of steps to make two strings equal if they are different in $$$m$$$ of the $$$n$$$ positions. We observe that $$$x_0 = 0$$$, $$$x_n = 1 + x_{n-1}$$$, and for all other $$$m$$$, we have $$$x_m = 1 + \frac{m}{n} x_{m-1} + \frac{n-m}{n} x_{m+1}.$$$ This is because there are $$$m$$$ positions that, if chosen, will change the character at that position from being different among the two strings to being the same, and $$$n-m$$$ positions at which changing the character will change that position from being the same across both strings to being different.
Now, iterating $$$m$$$ from $$$n$$$ to $$$1$$$, we can solve for each $$$x_m$$$ in terms of $$$x_{m-1}$$$. Afterwards, we can substitute $$$x_0 = 0$$$ into our equation for $$$x_1$$$, then substitute our value for $$$x_1$$$ into our equation for $$$x_2$$$, and so on to derive all of the $$$x$$$'s. Our answer is then $$$x_m$$$, where $$$m$$$ is the number of differences between the two input strings.
it's strange that no one got the third problem on Python
Quite a great contest! The D is a bit classic but the idea itself is quite great. Problem E is an interesting DS and tree problem but also a bit classic. (I mean the algorithm part) F is a dp on tree related to number theory but for me it's a little bit easier for the position of F. The diversity of algorithm is very great in this contest and hope you guys can do better next time.
In problem D how can we calculate F(1)
See my above comment: https://codeforces.com/blog/entry/112149?#comment-999324
Why is this solution for D not correct? Let C be the number of non equal indices.
We can only finish in the $$$C,2N-C,2N+C...$$$ moves. Assumption 1.
We call finish in any of the $$$C,2N+C,4N+..$$$ type moves odd type moves
We call finish in any of the $$$2N-C,4N-C,..$$$ type moves even type moves
The probability of finishing in C moves = $$$(C)!/N!$$$. -->(P2)
The probability of finishing in C moves = $$$(N-C)!*(C!)/N!$$$. -->(P1)
The probability of finishing in 2N-C moves = $$$(1-P1)*(P2)$$$.
Probability of finishing in $$$i^{th}$$$ odd move is $$$P2*(1-P1)^{2i}$$$ Probability of finishing in $$$i^{th}$$$ even move is $$$P2*(1-P1)^{2i+1}*(2N(i+1)-c)$$$
Summing moves*probability of odd type we get $$$\sum_{i=0}^{+\infty} P2*(1-P1)^{2i}*(2Ni+c)$$$
Summing moves*probability of even type we get $$$\sum_{i=0}^{+\infty} P2*(1-P1)^{2i+1}*(2N(i+1)-c)$$$
The expected odd sum is $$$(1-P1)^2*(2N*P2)/(1-(1-P1)^2)^2$$$ + $$$C*P1/(1-(1-P1)^2)$$$
The expected even sum is $$$(1-P1)^3*(2N*P2)/(1-(1-P1)^2)^2$$$ + $$$(2N-C)*P1*(1-P1)/(1-(1-P1)^2)$$$
Please let me know my arithmetic or logical mistake. Thanks
You can finish in $$$C, C+2, C+4, \ldots$$$ moves (not $$$2N - C$$$ and others). For example, suppose there are $$$11$$$ differences between $$$a$$$ and $$$b$$$. Then, you can verify that the number of moves needed can be any odd $$$k\ge 11$$$ (for example, to get $$$13$$$ first flip a bit to have $$$12$$$ differences, then go flip correct bits to go from $$$12$$$ to $$$0$$$ immediately).
l
Thank you so much for a fast editorial, problems were fun and informative to me, thanks a lot!!
The time complexity of C is not O(n*pow(2, min(u, k))) because we just need to check all subsets of length min(k, u) as the subsets of length < min(k, u) are a part of subsets of length min(k, u) and being able to change more letters is never going to bad
Hope this helps :)
You only choose subsets with length == k. And complexity will decrease enormously.
yep, see the edited version :)
A method to solve range basis query in $$$O(nlogn)$$$: (subtree and complement of subtree are weaker)
Iterate $$$r$$$, we maintain the lexicographically (by index) largest basis, then the query can be handled by simply ignoring all vectors with index less than $$$l$$$.
To maintain such basis, when you face two vectors on the same row, always keep the right one (one with larger index), because the left one can always use the right one to change itself.
star it = get it
If someone is interested in this technique, you can check out this problem: 1100F - Ivan and Burgers
I can't understand what mean by dp[u][d]=inf if (xu*xu) is not multiple of d.
Question f someone explain please
In problem F , why do we always perform the last move on the root vertex of the subtree while calculating dp?
Reason is this, 1) we can only apply one operation on a node. 2) let's say we apply i'th opertion on a root node , then we cannot apply any opertion on root. So last k-i operations are of no use. Why? because the remaining k-i operations has to be performed on the nodes except the root and our answer is dependent on the root node( which is = intial_val_of_root*max_gcd_of_root we get) which will never increase by the last k-i operations , that's it.
But actually, to make the GCD of the subtree of u equal to a multiple of d, we may use some operations in the subtree of u, but use no operation on u itself. Why can we ignore this case?
No I got stuck at B....
Pr**oblem D** There might be some wrong? **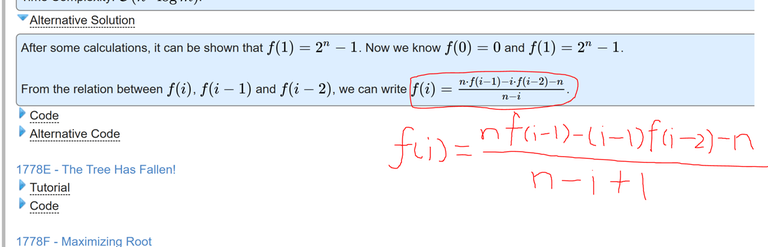
Fixed it. Thanks.
Are there any prerequisite topics we need to learn before attempting Problem D?
I am watching Errichto's videos about expected value (EV), which were on my watch later list but it seems like it is time to watch them.
any resoureces other than that ?.I am bad at math and very bad at expected values,probabilites
F can be solve in $$$O(n\times m)$$$ (Or $$$O(n\times mlog(m))$$$ ? Since I use a map to store the dp value) . Where $$$m$$$ is the number of divisors of $$$x_{1}$$$
Consider $$$dp_{u,x}$$$ as the same in the tutorial. Let $$$x = \prod{p_{i}^{d_{i}}}$$$, and $$$y = \prod{p_{i}^{\lceil \frac{d_{i}}{2} \rceil}}$$$, we only need to consider two cases: $$$dp_{u,x} = \sum{dp_{v,x}}$$$ and $$$dp_{u,x} = 1 + \sum{dp_{v,y}}$$$, where $$$v$$$ is all the children of vertex $$$u$$$. The first case represent we do not do any operation on vertex $$$u$$$, which requires $$$x | x_{u}$$$. The second case represent we do one operation on vertex $$$u$$$, which requires $$$y | x_{u}$$$. Special judge for $$$u=1$$$.
Why is that enough to only check the transition dp[v][x] -> dp[v][y] in the second case?
This is because y would be the smallest number whose square is a multiple of x. any other such number would end up being a multiple of y. and we know that for 2 numbers n1 and n2 such that n1 is a multiple of n2, dp[n2] <= dp[n1]
Lots of people are complaining about the contest but there are always people who complain. For me, the round was pretty good and I enjoyed problem C when I figured out how to solve it.
I agree. But I think the problem statements could have been made a little easier to understand.
What is complexity of C by backtracking solution given above? Is it O(n * pow(2, min(k,u))) because this code will generate all subsets of length <= min(k,u).
u = no. of unique character in string "a". k = min(u,k). usually we talk about worst case so it will be n*(pow(2,10)).But to be precise I think it will be n*pow(2,u).It is sure,we will go through all subsets of unique characters but for answer to be maximum we will consider only subsets having exactly k elements.Hope you will get.
I understood the solution but I am asking about time complexity of code
Can someone tell me why this code on problem D gets a TLE? https://codeforces.com/contest/1778/submission/191678717 Thank you very much if you can help me or give me some advice.
I found the size of array is too small just now -
such a joke
What a crap description of Problem B
First line they said you are given permutation of length n,an array of m distinct elements. I thought it is a permutation of m distinct integers of length n
I read this line around 3-4 times to wrap my head around
Then this negation effect, if you use negation you need to use bracket to make it clearer.
Even after seeing editorial, I did not understand what the question is asking until is saw a comment
is this Round 844 ? I am sorry Its Round (844+4)
Can anyone explain why sum decreases by 4 i ai=a(i+1)= 1 ?
Because if a[i] = a[i+1] =1 then you have already added 2 to the sum So you'll decrease sum by 2 then A[i] = A[i+1] = -1 after changing so you'll add -2 to the sum hence -2 + -2 = -4
In problem C, for the case when u=26, k=10 and n=1e5, won't the number of operations just blow up?
$$$n$$$*$$$26 \choose {10}$$$ $$$\approx$$$ $$$5e11$$$
There are atmost 10 different characters in string a,so the time complexity is atmost n*$$$\binom {10}{5}=1e5*252 \approx 2e6$$$
Misunderstood the problem, I thought 10 is the number of characters in A which are different from B. Thanks, for the correction!!
Shouldn't complexity in E be $$$O(nlog^2(d))$$$, where $$$d=max(a_i)$$$ not $$$d=log(max(a_i))$$$?
Yeah. Fixed it. Thanks.
probably it's late but I have another solution for problem D which I think it's more easier ,it depends on linearity of expectation.
Let $$$rem$$$ to be the number of positions that have $$$a_i \neq b_i$$$ and $$$n$$$ is the size of strings.
let $$$dp_i$$$ the expected number of flips to go from state $$$i$$$ to $$$i-1$$$ .
let $$$p_i$$$ the probability of selecting non-equal position which will $$$p_i=\frac{i}{n}$$$ .
By linearity of expectation ,the answer is $$$\sum_{i=1}^{i=rem}dp_i$$$ .
We will calculate $$$dp_i$$$ from this formula $$$dp_i= p_i .1 +(1-p_i)(1+dp_{i+1}+dp_i)$$$ and then simplifying $$$dp_i= \frac{1+(1-p_i).dp_{i+1}}{p_i}$$$.
finally the base case is $$$dp_n=1$$$ because in this state we will definitely go to state $$$dp_{i-1}$$$ only.
Sorry for my bad english it's my first try for explanation.
great explanation ..
I have a question please help in problem d
We get, ai=n+i⋅ai−1n−i⋅bi−1 and bi=n−in−i⋅bi−1 for 2≤i≤n.
f(i)=ai+bi⋅f(i+1).
so why can't be just get value of f(i+1) directly
f(i+1) = (f(i)- ai ) / bi
Why can't we directly find value like this?
Great problems. Really enjoyed the round despite struggling with B for way too long.
How can this solution still be too slow for Test #30 in problem C? (PyPy 3) Any way I can write the for-loop faster.
https://codeforces.com/contest/1778/submission/191729330
Isn't the worst case time complexity for C : O(2kn)
I think because of the:
"if sum(cc) == k:"
you will only get a time complexity of 252 * n. ( 10!/(5!*5!) = 252 )
Okay that makes sense, but there are still 2e7 operations at max which I think is a lot for 2 seconds when doing recursion.
Very true. Thank you for you helpful answer!
Got clarified thanks
I see a lot of comments for problem D, I found the alternative approach pretty interesting so I made a video on it, you can find this on the channel- here . If the video doesn't show up then please wait for a while as YT sometimes takes a bit long to process it.
Happy coding :)
How did one can come to conclusion to write f(x) = ai + bi*f(i-1) by just seeing one value for f(2) ? We already have equation f(i) = 1+ A*f(i-1)+B*f(i+1) form right ? so just concluding that f(i) just depends only on f(i-1) by taking one example of f(2) sounds unintuitive to me
This worked for problem D so maybe it will work for problem E... Geothermal can you please explain you solution for problem E? I think people (myself) would be interested in knowing how it works.
For the most part, my solution is equivalent to the model solution: in particular, I compute subtree XOR bases and use them to answer queries where the root is equal to or outside the subtree of our given vertex.
The component of my solution that differs from my solution is the case where the root is in the subtree of our vertex. Let c be the child of our vertex whose subtree contains the root; we can find c by binary searching on the pre-order traversal. We note that we are essentially computing the maximum XOR of all vertices outside the subtree of c. The model solution thus precomputes XOR bases for all prefixes and suffixes of the preorder traversal, then merges the bases for the prefix and suffix excluding the subtree of c to compute the answer.
My solution instead uses rerooting DP to directly compute the XOR basis of all vertices outside the subtree of c for each vertex c in the tree. To perform the rerooting, I use a similar prefix basis/suffix basis idea: for each vertex, I merge the XOR bases for each prefix and suffix of its children; then, to go from a vertex to its child, I merge the XOR basis containing v and vertices outside the subtree of v with appropriate prefix and suffix bases.
I think the model solution is much more elegant and easier to implement than mine; I would have implemented it had I thought of it in contest. Unfortunately, I was being a bit silly, so this is what I ended up with :)
Ah that makes a lot of sense. So instead of using the euler tour for computing your prefix and suffix XOR basis you did it directly on the children of each node and found a way to transition using the prefix and suffix XOR basis of the node's siblings, nice.
I agree it's not as clean, but I think it's a cool idea. Thanks for sharing.
Problem D reminded me of https://codeforces.com/contest/1753/problem/C
Has this round been unrated? My rating still keeps unchanged yet!
when will the contest rating be shown to us??
C is very strange. O(10^8) solution is also working which I think usually do not work. Moreover, I found many solutions which were accepted during contest but after contest giving TLE. One more thing my solution is accepted only after I passed the vector by reference to the recursive funtion.
Don't forget to update the rating of #848 for me later. I was in div1 when registered in this contest, but that's because my negative rating in TypeDB round was rolled back temporarily, and I should be counted as div2 in this contest. MikeMirzayanov
There are certain solutions for problem c which have been tested for28 test cases only whereas there are others which are tested for 38 test cases. Some solutions which were accepted during the contest are giving tle right now when submitted.
I noticed this too, my C passed main tests with 500 ms but now barely squeaks by with 1950 ms.
Here are two submission for c. Both are same but one which was accepted during contest is still accepted while I copy pasted it and it is giving TLE.
Accepted Submission : https://codeforces.com/contest/1778/submission/191808748
My Submission : https://codeforces.com/contest/1778/submission/192095509 giving TLE
Is this solution for problem D correct.Let us call the bits that are not same in A and B as different bits and the bits that are same in A and B as same bits. We know that the no of moves to make the two strings can be $$$K + 2 t$$$ where $$$t>=0$$$ and $$$K$$$ is the no of different bits.
We can find the expected value by summing the terms prob(it takes i moves to make the two strings equal)*i . We can see that we have to flip the different bits odd no of times and the same bits even no of times . So we can calculate the probability of taking i moves to make the two strings same by solving the integral equation and multiply it with $$$(1/n)^i$$$ as we are making i moves . The integral equation is $$$(2k_1+1)+(2k_2+1)+....+(2k_n) = i$$$ where the odd terms corresspond to diff bits and even terms to same bits. The solution of this integral equation will be $$${C_{n -1 }^{n-1 + \dfrac{i-k} {2}}}$$$
So the final formula is $$${\sum_{t = 0}^\infty \dfrac{K+ 2t} {n^{2t+K}} C_{t}^{n+t-1}}$$$ Is there any way to proceed from this as this summation is involving infinite terms
192167224 why is this TLE ? How do I improve it? Div2D
Bangladeshi Guys. Wow
Hey can anyone explain the intuition behind problem A shy the sum is reduced by 4 and increased by 4 ?
Problem F can also be done with a brainless $$$O(36*36*n)$$$ 5D dp if you observe that only the prime factors of the root node's value matter, and each node's value has atmost 4 unique prime factors.
The dp state will be: $$$dp[v][p][q][r][s]$$$ which holds the minimum number of moves required to make the lowest frequency in any node in subtree of $$$v$$$ of the $$$1$$$'st till the $$$4$$$'th prime factor equal to $$$p$$$, $$$q$$$, $$$r$$$ and $$$s$$$ respectively (minimums can occur in different nodes for different prime factors).
Implementation:link
adnan_toky Suppose in question C we take U = 26 and K = 10 . Will the #operations won’t go over 10^10 ?
okay got it !
Sorry for disturbing old discussion but could anyone explain how Red people or black-red people have used bitmasking in Problem C? Brute force is pretty simple but i don't get the mask idea. This is jiangly's submission which i do not seem to understand properly? why is he comparing the number of bits set in K with the number of bits set for a particular alphabet frequency. 191557742