Hope you liked the problems! We apologize for the (very?) weak tests in H.
Editorials for problems will be added over time (and hints), for now, please take a look at the available hints and model solutions.
ForceCodes is a reference CrossCode, you should try it.
Basil is one of the characters in OMORI, you should also try it.
"World is Mine" is one of Hatsune Miku's most well known songs, and a fan-made MV has a lot of cakes in it) I originally wanted to make the characters names Miku and Sweetheart(from OMORI), but decided to stick to Alice and Bob to keep the statement clean.
The epigraph is a reference to KonoSuba.
The epigraph is a quote from Celeste (you should try it), and the title is a reference to one of it's locations, Mirror Temple, but only now there are fumo dolls in it)
Your strategy is to upload more RAM as soon as you can upload.
You will upload on the seconds $$$1, k + 1, 2k + 1, 3k + 1 \ldots$$$.
#include <bits/stdc++.h>
#define all(x) (x).begin(), (x).end()
#define allr(x) (x).rbegin(), (x).rend()
const char nl = '\n';
typedef long long ll;
typedef long double ld;
using namespace std;
void solve() {
int n, k;
cin >> n >> k;
cout << 1 + (n - 1) * k << nl;
}
int main() {
ios::sync_with_stdio(0); cin.tie(0);
int t;
cin >> t;
while (t--) {
solve();
}
}
Try solving the problem if instead of paying $$$k + 1$$$ coins, you pay $$$k$$$ coins.
What if you pay only $$$1$$$ coin per operation?
Can you add the answers to the $$$k$$$ coins per operation problem and $$$1$$$ coin per operation problem to get the answer?
#include <bits/stdc++.h>
#define all(x) (x).begin(), (x).end()
#define allr(x) (x).rbegin(), (x).rend()
const char nl = '\n';
typedef long long ll;
typedef long double ld;
using namespace std;
void solve() {
int n;
cin >> n;
vector<int> a(n);
for (int i = 0; i < n; i++) cin >> a[i];
ll pref_max = 0, s = 0, mx = 0;
for (int i = 0; i < n; i++) {
pref_max = max(pref_max, (ll) a[i]);
ll d = pref_max - a[i];
s += d;
mx = max(mx, d);
}
cout << s + mx << nl;
}
int main() {
ios::sync_with_stdio(0); cin.tie(0);
int T;
cin >> T;
while (T--) {
solve();
}
}
When will $$$h_n$$$ first become equal to zero?
When will $$$h_{n-1}$$$ first become equal to zero?
Consider solving from right to left.
Suppose you want to find when $$$h_i$$$ will fist be equal to zero. Try splitting into the cases $$$h_i = h_{i+1}$$$ at some point (before both are zero) and when that is not true.
#include <bits/stdc++.h>
#define all(x) (x).begin(), (x).end()
#define allr(x) (x).rbegin(), (x).rend()
const char nl = '\n';
typedef long long ll;
typedef long double ld;
using namespace std;
void solve() {
int n;
cin >> n;
vector<int> h(n);
for (auto &x: h) cin >> x;
int ans = h[n - 1];
for (int i = n - 2; i >= 0; i--) {
ans = max(ans + 1, h[i]);
}
cout << ans << nl;
}
int main() {
ios::sync_with_stdio(0); cin.tie(0);
int T;
cin >> T;
while (T--) solve();
}
Alice's optimal strategy is simple (and kind of fixed).
Alice always eats the least tasty cake that she can eat.
Convert the given array to it's count array $$$c_i$$$, for example, the array $$$[1, 5, 1, 2, 1, 5, 1]$$$ becomes $$$[4, 1, 2]$$$.
Consider a set of $$$k$$$ indices that Bob will choose to eat ($$$c_{i_1} + ... + c_{i_k}$$$ cakes in total). What are the necessary conditions for him to be able to do that?
For a set of $$$k$$$ indices $$$1 \le i_1 \le i_2 \le \ldots \le i_k \le |c|$$$, the condition $$$\sum_{j=1}^{p}{c_{i_j}} \le i_p - p$$$ must hold for all $$$1 \le p \le k$$$.
#include <bits/stdc++.h>
#define all(x) (x).begin(), (x).end()
#define allr(x) (x).rbegin(), (x).rend()
const char nl = '\n';
typedef long long ll;
typedef long double ld;
using namespace std;
const int inf = 1e9;
void solve() {
vector<int> a;
{
int n;
cin >> n;
map<int, int> cnt;
while (n--) {
int x;
cin >> x;
cnt[x]++;
}
for (auto const &[k, v]: cnt) {
a.push_back(v);
}
}
int n = a.size();
vector<int> dp(n + 1, inf);
dp[0] = 0;
for (int i = 1; i <= n; i++) {
vector<int> ndp = dp;
for (int k = 1; k <= n; k++) {
int nv = dp[k - 1] + a[i - 1];
if (nv <= i - k) {
ndp[k] = min(ndp[k], nv);
}
}
dp = ndp;
}
int ans = n;
while (dp[ans] >= inf) ans--;
cout << n - ans << nl;
}
int main() {
ios::sync_with_stdio(0); cin.tie(0);
int T;
cin >> T;
while (T--) solve();
}
Let $$$b_v = \displaystyle{\sum_{u \in L}{a_u} - a_v}$$$ if $$$L$$$ is not empty and $$$+\infty$$$ otherwise. What does the operation do to the values of $$$b$$$? What does the objective change to?
Let $$$v$$$ be an ancestor of $$$w$$$ and $$$d_v < d_w$$$ ($$$d$$$ is the depth array). Then, you can add $$$1$$$ to $$$b_v$$$ and subtract $$$1$$$ from $$$b_w$$$ in $$$d_w - d_v$$$ operations. Let this be our new operation on a pair of vertices $$$(v, w)$$$.
Suppose one optimal sequence of operations uses it on $$$(v_1, w_1)$$$ and $$$(v_2, w_2)$$$, and the paths $$$v_1 \rightarrow w_1$$$ and $$$v_2 \rightarrow w_2$$$ intersect. Let $$$d_{v1} \le d_{v2}$$$. Then, if $$$d_{w1} \le d_{w2}$$$, it is not less optimal to apply the operation on $$$(v_1, w_2)$$$ and $$$(v_2, w_1)$$$.
#include <bits/stdc++.h>
#define all(x) (x).begin(), (x).end()
#define allr(x) (x).rbegin(), (x).rend()
const char nl = '\n';
typedef long long ll;
typedef long double ld;
using namespace std;
const ll inf = 1e15;
void solve() {
int n;
cin >> n;
vector<int> a(n);
for (auto &x: a) cin >> x;
vector<int> d(n);
vector<vector<int>> g(n);
for (int i = 1; i < n; i++) {
int p;
cin >> p;
p--;
g[p].push_back(i);
d[i] = d[p] + 1;
}
vector<ll> b(n); // b[v] = sum(a[u]) - a[v]
for (int v = 0; v < n; v++) {
if (g[v].empty()) {
b[v] = inf;
} else {
b[v] = -a[v];
for (int u: g[v]) {
b[v] += a[u];
}
}
}
ll ans = 0;
for (int v = n - 1; v >= 0; v--) {
queue<int> q;
q.push(v);
while (!q.empty()) {
int i = q.front();
q.pop();
for (int u: g[i]) {
ll delta = min(-b[v], b[u]);
if (delta > 0) {
b[v] += delta;
b[u] -= delta;
ans += delta * (d[u] - d[v]);
}
q.push(u);
}
}
}
cout << ans << nl;
}
int main() {
ios::sync_with_stdio(0); cin.tie(0);
int T;
cin >> T;
while (T--) {
solve();
}
}
1987F1 - Interesting Problem (Easy Version) and 1987F2 - Interesting Problem (Hard Version)
Does the operation have any connection to balanced bracket sequences?
#include <bits/stdc++.h>
#define all(x) (x).begin(), (x).end()
#define allr(x) (x).rbegin(), (x).rend()
const char nl = '\n';
typedef long long ll;
typedef long double ld;
using namespace std;
const int inf = 1e9;
void solve() {
int n;
cin >> n;
vector<int> a(n);
for (int i = 0; i < n; i++) cin >> a[i];
vector<vector<int>> dp(n + 1, vector<int> (n + 1, inf));
for (int i = 0; i <= n; i++) {
dp[i][i] = 0;
}
for (int le = 1; le <= n; le++) {
for (int l = 0; l + le <= n; l++) {
if (a[l] % 2 != (l + 1) % 2) continue;
if (a[l] > l + 1) continue;
int v = (l + 1 - a[l]) / 2;
int r = l + le;
for (int m = l + 1; m < r; m += 2) { // index of the closing bracket
if (dp[l + 1][m] <= v) {
int new_val = max(v, dp[m + 1][r] - (m - l + 1) / 2);
dp[l][r] = min(dp[l][r], new_val);
}
}
}
}
vector<int> dp2(n + 1);
for (int i = 0; i < n; i++) {
dp2[i + 1] = dp2[i];
for (int j = 0; j < i; j++) {
if (dp[j][i + 1] <= dp2[j]) {
dp2[i + 1] = max(dp2[i + 1], dp2[j] + (i - j + 1) / 2);
}
}
}
cout << dp2[n] << nl;
}
int main() {
ios::sync_with_stdio(0); cin.tie(0);
int T;
cin >> T;
while (T--) {
solve();
}
}
1987G1 - Spinning Round (Easy Version)
Consider that the edges are directed from $$$i \to l_i$$$ or $$$i \to r_i$$$ respectively. So that edges point from vertices with smaller values to vertices with larger values. That is $$$a \to b$$$ implies that $$$p_a < p_b$$$.
Notice that by definition, every vertex must have only $$$1$$$ edge that is going out of it. Therefore, if we consider the diameter to be something like $$$v_1 \to v_2 \to v_3 \to \ldots \to v_k \leftarrow \ldots \leftarrow v_{d-1} \leftarrow v_{d}$$$, since it is impossible for there to be some $$$\leftarrow v_i \to$$$ since each vertex has exactly one edge going out of it.
Therefore, it makes that we can split the path into 2 distinct parts: - $$$v_1 \to v_2 \to v_3 \to \ldots \to v_k$$$ - $$$v_d \to v_{d-1} \to \ldots \to v_{k}$$$
I claim that I can choose some $$$m$$$ such that the path $$$v_1 \to v_2 \to v_3 \to \ldots \to v_{k-1}$$$ and $$$v_d \to v_{d-1} \to \ldots \to v_{k+1}$$$ are in the range $$$[1,m]$$$ and $$$[m+1,n]$$$ or vice versa. That we are able to cut the array into half and each path will stay on their side.
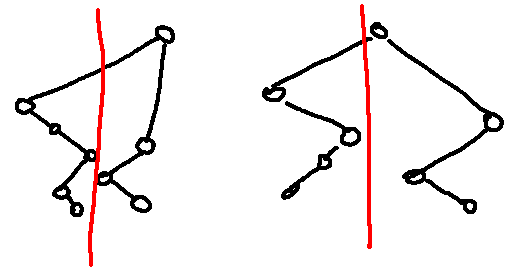
The red line shown above is the cutting line, as described. Proof is at the bottom under Proof 1 for completeness.
Now, we want to use this idea to make a meet in the middle solutions where we merge max stacks from both sides. Specifically: - maintain a max stack of elements as we are sweeping from $$$i=1\ldots n$$$. - for each element on the max stack, maintain the maximum size of a path that is rooted on that element.
Here is an example with $$$p=[4,1,5,3,2,6]$$$
- $$$i=1$$$: $$$s=[(4,1)]$$$
- $$$i=2$$$: $$$s=[(4,2),(1,1)]$$$
- $$$i=3$$$: $$$s=[(5,3)]$$$
- $$$i=4$$$: $$$s=[(5,3),(3,1)]$$$
- $$$i=5$$$: $$$s=[(5,3),(3,2),(2,1)]$$$
- $$$i=6$$$: $$$s=[(6,4)]$$$
When we insert a new element $$$x$$$, we pop all $$$(p_i,val)$$$ with $$$p_i < p_x$$$ and add in $$$(x,\max(val)+1)$$$ into the stack. Now, all elements of the stack has to updated with $$$s_{i,1} := \max(s_{i,1},s_{i+1,1}+1)$$$, which is really updating a suffix of $$$s_{*,1}$$$ with $$$val+k,\ldots,val+1,val$$$.
Firstly, it is clear that the $$$2$$$ vertices we merge, should have the biggest $$$p_i$$$ value, since a bigger $$$p_i$$$ value implies a bigger path size.
What we care about is the biggest path size possible only using vertices on $$$[1,i]$$$, which we denote array $$$best$$$. In the above example, $$$best = [1,2,3,3,4]$$$. We really only care about obtaining the array $$$best$$$ and not $$$s$$$. We can find this array in $$$O(n \log n)$$$ using segment trees or even in $$$O(n)$$$.
However, we cannot directly take the biggest values on each side. Consider $$$p=[2,1\mid,3,4]$$$. On the left and right side, the max stacks are $$$[2,1]$$$ and $$$[4,3]$$$ respectively, but we cannot connect $$$2$$$ with $$$4$$$ since the $$$3$$$ is blocking the $$$2$$$.
Suppose $$$a_1,a_2,\ldots,a_s$$$ are the prefix maximums while $$$b_1,b_2,\ldots,b_t$$$ are the suffix maximums.
Then, if the dividing line is at $$$a_i \leq m < a_{i+1}$$$, we will merge $$$a_i$$$ on the left side with $$$a_{i+1}$$$ on the right side. Similarly, if the dividing line is at $$$b_i \leq m < b_{i+1}$$$, we will merge $$$b_i$$$ on the left side with $$$b_{i+1}$$$ on the right side.
So, if $$$a_i \leq m < a_{i+1}$$$, it is equivalent to merging the best path on $$$[1,m]$$$ and $$$(m,a_{i+1})$$$ since then $$$a_{i+1}$$$ will be the root of the best path on the right side. It is similar for $$$b_i \leq m < b_{i+1}$$$.
Actually, we can prove that instead of $$$(m,a_{i+1})$$$, $$$(m,a_{i})$$$ is enough, and the proof is left as an exercise.
The total complexity becomes $$$O(n \log n)$$$ or $$$O(n)$$$ depending on how quickly array $$$best$$$ is found for subarrays.
Proof 1
Suppose that there are 2 paths $$$a_1 \to a_2 \to \ldots \to a_s$$$ and $$$b_1 \to b_2 \to \ldots \to b_t$$$, $$$a_1 < b_1$$$, and $$$a_s = b_t$$$ but they do not intersect at any vertices other vertices. Then we will prove that there is no such case where $$$a_s' > b_t'$$$.
Suppose that it is true that we can find some $$$a_{s'} > b_{t'}$$$.
Let $$$(s',t')$$$ be the minimum counterexample so that $$$a_{s'} > b_{t'}$$$ but $$$a_{s'-1}<b_{t}$$$. Therefore, we have $$$a_{s'-1} < b_t < a_{s'}$$$. By definition, that $$$r_{a_{s'-1}} = a_{s'}$$$, we have $$$p_{b_t} < p_{a_{s'-1}}$$$.
Then, $$$a_s$$$ cannot be in between $$$a_{s'-1}$$$ and $$$a_{s'}$$$ or else $$$r_{a_{s'-1}} = a_{s} \neq a_{s'}$$$. But, then we need to find a path from $$$b_{t'}$$$ to $$$b_{t}=a_{s}$$$ which does not touch either $$$a_{s'-1}$$$ or $$$a_{s'}$$$ which is impossible.
#include <bits/stdc++.h>
using namespace std;
#define ii pair<int,int>
#define fi first
#define se second
#define pub push_back
#define pob pop_back
#define rep(x,start,end) for(int x=(start)-((start)>(end));x!=(end)-((start)>(end));((start)<(end)?x++:x--))
#define sz(x) (int)(x).size()
int n;
int arr[400005];
string s;
int ans[2][400005];
int t[400005];
vector<int> stk[2];
vector<ii> process(int l,int r,int val[]){
vector<ii> v;
int curr=0;
rep(x,l,r+1){
ii res={x,0};
while (!v.empty() && arr[v.back().fi]<arr[x]){
int t=v.back().se; v.pob();
if (!v.empty()) v.back().se=max(v.back().se,t+1);
res.se=max(res.se,t+1);
}
v.pub(res);
curr=max(curr,res.se+sz(v));
val[x]=curr;
}
return v;
}
signed main(){
ios::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
cin.exceptions(ios::badbit | ios::failbit);
int TC;
cin>>TC;
while (TC--){
cin>>n;
rep(x,1,n+1) cin>>arr[x];
cin>>s;
rep(z,0,2){
auto v=process(1,n,ans[z]);
stk[z].clear();
for (auto [a,b]:v) stk[z].pub(a);
reverse(arr+1,arr+n+1);
}
int mx=ans[0][stk[0][0]]+ans[1][n-stk[0][0]+1]-1;
rep(z,0,2){
rep(x,0,sz(stk[z])-1){
process(stk[z][x],stk[z][x+1],t);
rep(y,stk[z][x],stk[z][x+1]) mx=max(mx,t[y]+ans[z^1][n-y]);
}
reverse(arr+1,arr+n+1);
}
cout<<mx-1<<endl;
}
}
1987G2 - Spinning Round (Hard Version)
#include <bits/stdc++.h>
#define all(x) (x).begin(), (x).end()
#define allr(x) (x).rbegin(), (x).rend()
const char nl = '\n';
typedef long long ll;
typedef long double ld;
using namespace std;
array<vector<int>, 2> get_l_and_r(vector<int> &p) {
int n = p.size();
vector<int> l(n), r(n);
stack<int> s;
for (int i = 0; i < n; i++) {
while (!s.empty() && p[s.top()] < p[i]) s.pop();
if (s.empty()) l[i] = -1;
else l[i] = s.top();
s.push(i);
}
s = {};
for (int i = n - 1; i >= 0; i--) {
while (!s.empty() && p[s.top()] < p[i]) s.pop();
if (s.empty()) r[i] = n;
else r[i] = s.top();
s.push(i);
}
return {l, r};
}
int ans_l_edge(array<int, 2> d, array<int, 2> e) {
return d[0] + 1 + max(d[1], e[0]);
}
int ans_r_edge(array<int, 2> d, array<int, 2> e) {
return e[1] + 1 + max(d[1], e[0]);
}
array<int, 2> add_l_edge(array<int, 2> d, array<int, 2> e) {
return {max({d[0], d[1] + 1, e[0] + 1}), e[1]};
}
array<int, 2> add_r_edge(array<int, 2> d, array<int, 2> e) {
return {d[0], max({d[1] + 1, e[0] + 1, e[1]})};
}
vector<array<int, 2>> process_dp(vector<array<int, 2>> &dp) {
array<int, 2> max_a = {-1, -1}, max_b = {-1, -1}, max_s = {-1, -1};
for (auto [a, b]: dp) {
if (a > max_a[0] || (a == max_a[0] && b > max_a[1])) {
max_a = {a, b};
}
if (b > max_b[1] || (b == max_b[1] && a > max_b[0])) {
max_b = {a, b};
}
if (a + b > max_s[0] + max_s[1]) {
max_s = {a, b};
}
}
return {max_a, max_b, max_s};
}
void add_to_map(map<array<int, 2>, int> &dp_ind, int &len_dp, array<int, 2> a) {
if (!dp_ind.count(a)) {
dp_ind[a] = len_dp++;
}
}
void solve() {
int n;
cin >> n;
vector<int> p(n);
for (int i = 0; i < n; i++) cin >> p[i];
string s;
cin >> s;
auto [l, r] = get_l_and_r(p);
for (int i = 0; i < n; i++) {
if (p[i] == n) continue;
if (l[i] == -1 && s[i] == 'L') {
cout << -1 << nl;
return;
}
if (r[i] == n && s[i] == 'R') {
cout << -1 << nl;
return;
}
}
int ans = 0;
vector<int> q(n + 1);
for (int i = 0; i < n; i++) {
q[p[i]] = i;
}
int len_dp = 0;
map<array<int, 2>, int> dp_ind;
for (int x = 1; x <= n; x++) {
int i = q[x];
int tl = l[i], tr = r[i];
add_to_map(dp_ind, len_dp, {tl, i});
add_to_map(dp_ind, len_dp, {i, tr});
add_to_map(dp_ind, len_dp, {tl, tr});
}
vector<vector<array<int, 2>>> dp(len_dp, {{0, 0}});
for (int x = 1; x <= n; x++) {
int i = q[x];
int tl = l[i], tr = r[i];
int ind_l = dp_ind[{tl, i}];
int ind_r = dp_ind[{i, tr}];
int ind_c = dp_ind[{tl, tr}];
for (auto const &d: dp[ind_l]) {
for (auto const &e: dp[ind_r]) {
ans = max(ans, d[1] + e[0]);
if (tl >= 0 && s[i] != 'R') {
ans = max(ans, ans_l_edge(d, e));
dp[ind_c].push_back(add_l_edge(d, e));
}
if (tr <= n - 1 && s[i] != 'L') {
ans = max(ans, ans_r_edge(d, e));
dp[ind_c].push_back(add_r_edge(d, e));
}
}
}
dp[ind_c] = process_dp(dp[ind_c]);
}
cout << ans << nl;
}
int main() {
ios::sync_with_stdio(0); cin.tie(0);
int T;
cin >> T;
while (T--) {
solve();
}
}
Think of the query result as some number between $$$|i - i_0| + |j - j_0|$$$ and $$$|i - i_0| + |j - j_0| + (|i - i_0| + 1) \cdot (|j - j_0| + 1)$$$.
Try solving for $$$n = 1$$$.
Try solving in $$$n \log_2(m)$$$ queries (might be useful later)
#include <bits/stdc++.h>
#define all(x) (x).begin(), (x).end()
#define allr(x) (x).rbegin(), (x).rend()
const char nl = '\n';
typedef long long ll;
typedef long double ld;
using namespace std;
int ans_x = 0, ans_y = 0, cnt_q = 0;
// Coordinates are flipped
int query(int x, int y) {
cnt_q++;
int res = 0;
cout << "? " << y << ' ' << x << endl;
cout.flush();
cin >> res;
if (res < 0) {
exit(0);
}
if (res == 0) {
ans_x = x;
ans_y = y;
}
return res;
}
/* Explanation:
* Splits the stripe of three into |a-O-a-b-O-b-a-O-a|.
* O are the three query points (all in the same column).
* Cons: hard to correctly account for errors in a non-bruteforce way.
* Pros: gives a better constant factor (3 / 4 of the original length)
* Number of queries: n + 3 * 21 + 25 * ceil(log(25, 2)) + eps
* Though the binary search part uses less queries than that */
void f(int lx, int rx, int ly, int ry) {
int n = rx - lx + 1;
// Bruteforce base case (uses binary search)
if (n <= 25) { // can be n <= 22 or above
for (int x = lx; x <= rx; x++) {
int lb = ly, ub = ry;
while (lb <= ub) {
int res = query(x, lb);
int low_y = ((res - 1) + 1) / 2, high_y = res;
int new_lb = lb + max(1, low_y), new_ub = min(ub, lb + high_y);
lb = new_lb;
ub = new_ub;
}
}
return;
}
// Here, (2a - 1) + (2b - 1) + (2a - 1) = n
int a = 3 * (n + 3) / 16;
int y = min(ry, ly + 1);
int x1 = lx + a - 1;
x1 = max(x1, lx);
x1 = min(x1, rx);
int x2 = (lx + rx) / 2;
x2 = max(x2, x1 + 1);
x2 = min(x2, rx);
int x3 = rx - a + 1;
x3 = max(x3, x2 + 1);
x3 = min(x3, rx);
int m = min(3, ry - ly + 1);
vector<vector<bool>> good(n, vector<bool> (m, true));
int new_lx = lx, new_rx = rx;
int new_ly = ly, new_ry = ry;
for (int x: {x1, x2, x3}) {
int res = query(x, y);
new_lx = max(new_lx, x - res);
new_rx = min(new_rx, x + res);
new_ly = max(new_ly, y - res);
new_ry = min(new_ry, y + res);
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
int r_x = lx + i, r_y = ly + j;
int dx = abs(r_x - x);
int dy = abs(r_y - y);
int d = dx + dy;
int S = (dx + 1) * (dy + 1);
// d <= res <= d + S must hold
if (res < d || d + S < res) {
good[i][j] = false;
}
}
}
}
bool has_good = false;
for (auto vx: good) {
for (auto vy: vx) {
if (vy) {
has_good = true;
}
}
}
good.clear();
good.shrink_to_fit();
if (has_good) {
f(new_lx, new_rx, new_ly, new_ry);
} else {
f(lx, rx, ly + m, ry);
}
}
void solve() {
int n, m;
cin >> n >> m;
ans_x = 0; ans_y = 0; cnt_q = 0;
f(1, m, 1, n);
cout << "! " << ans_y << ' ' << ans_x << endl;
cout.flush();
cerr << n << ' ' << cnt_q << " | " << n + 225 << endl;
}
int main() {
ios::sync_with_stdio(0); cin.tie(0);
int T;
cin >> T;
while (T--) {
solve();
}
}










Tutorials are broken
If an editorial isn't showing properly, it should be because there currently isn't one.
Oh alright, thanks for the great contest btw :)
Can someone please explain why greedy won't work for D? My solution: https://codeforces.com/contest/1987/submission/268165706
This is the exact greedy solution I did.But not able to figure out why it fails.
Did you remember monotonicity? I messed up b/c of it.
Sorting by freq won't work here as someone with higher freq that has a lower tastiness would be eaten by alice which could be prevented by bob by eating that first
Check for this frequency array F = {4, 4, 4, 3, 5, 5, 2}
Correct answer is 5
Sort: 2 3 4 4 4 5 5
Alice: 2
Bob: 3
Alice: 4
Bob: 5
Alice: 5
Bob: rest two 4's
So Alice will get total 3 cakes. This is what i was trying greedily but it didn't worked, can you tell me what i am doing wrong here?
Given array F is Frequency array, not the array containing tastiness values of the cakes. F[i] contains number of cake with tastiness value i.
Check this comment
Let the array you mentioned is tastiness array, then is my approach correct?
Or let tastiness = {4,3,2,5,6,8,3,4} then after sorting:
2 3 3 4 4 5 6 8
A/c to my approach:
Alice: 2 Bob: 5 Alice: 3 Bob: 6 Alice: 4 Bob: 8
Now Alice can't choose any so total she will choose 3 cakes.
Is this a correct approach, Bob will choose the cake whose frequency is as minimum as possible and greater than Alice's last chosen cake.
This approach wouldn't work always.
Check for this = {1 1 1 1 2 2 2 2 3 3 3 3 4 4 4 5 5 5 5 5 6 6 6 6 6 7 7}
According to your approach, Bob will start with 7 but optimal is start with 4 and complete it then take 7.
Got it, thanks!
My approach is as follows:
Alice 1 Bob 4 Alice 2 Bob 4 Alice 3 Bob 4 Alice 5 Bob 7 Alice 6 Bob 7 But I get wrong answer on test 2. 268201241 Can you help, please?
Please simulate the last test case to know why greedy won't work.
Problem G1 coincides with QOJ 3797 Wireless Communication Network.
Seems like G1 unfortunately does :( The subtask was added later to help balance the problemset and we weren't aware of such a coincidence.
Problem D. World is Mine ***** 2 pointer approach -> sorting the array -> (i)one pointer of alice is on left -> (j)bob's pointer is on right . HashSet -> cakes have been eaten by the alice -> i encounters a cake at a[i] -> if the a[i] is already present in the set -> not present -> cake is added in set -> j encounters a cake at a[j] . didn't work can anyone pls tell me why.
I have a $$$O\left(n \log n\right)$$$ solution for D. https://codeforces.com/contest/1987/submission/268177088
can you please explain?
ok! Obviously, we need to iterate through all the elements in smallest-to-largest order to simulate Alice's choices, and I'm using a std::map to keep track of how many of each number there are for subsequent calculations. First, I'll try to have Bob try to stop Alice from selecting the current element every time, and for convenience we'll write the number of times the current number occurs as $$$c$$$. This requires that Bob has been unable to stop Alice at least $$$c$$$ times before, so we'll maintain a variable ("hv" in the code) representing the number of times Bob has been unable to stop Alice. But the above is clearly wrong. We need to reverse the operation. Specifically, if we are now certain that we cannot stop Alice, we replace this operation with the previous successful stopping operation, the most consumed one, if that is preferable. In the code, I use a std::multiset to keep track of successful blocking operations.
I wrote a version with comments, which should be easier to understand https://codeforces.com/contest/1987/submission/268356662 I understand this as there might be a tastiness appears later, that costs less "skip points" than the skip before, so you record all the skip happen in the previous, and keeps finding for better solution which costs less rounds for b that happens later
nice problem h guys, really appreciate your testing
yes, it seems that they just generated 300+ random tests and thought "hmmm, maybe on some test the square will get a time limit")))
268226747
It seems like this solution uses no more than $$$50$$$ queries on the current data. Can anyone construct a counter-test?
Sure.
Cool. Do you have any estimate of how many queries are used for the test you constructed (as a function of $$$N$$$)?
I guess $$$\mathcal{O}(\sqrt{N})$$$? The idea is to have a square of $$$1$$$s in the corner (and also the hidden cell there). So almost wherever you ask, you see something around $$$x+y+(\sqrt{N})^2$$$, so it only tells you that the hidden cell is not in this area (so you discard around $$$N$$$ cells, but we can show better). What gives you more information is asking about a rectangle that won't contain all $$$1$$$s. My initial idea was that if we get an answer larger than $$$N$$$, then we discard the area around the queried cell (hopefully discarding around $$$N$$$ cells), and if we get an answer smaller than $$$N$$$, then we restrict ourselves to a square (hopefully decreasing the number of cells geometrically). But yeah, it seems that it's even better. Also Idk what about $$$M$$$ much larger than $$$N$$$, probably you can show something too. I was mostly worried about TL and spent most of the time thinking how to optimize it, but it just passed, so...
Oh, actually (on a square grid) response greater than $$$N$$$ tells you that you can discard around $$$N \log (N)$$$ cells (a shape enclosed by hyperbolas).
E can be solved in $$$O(N\log N)$$$ time by replacing the vectors in my solution 268156681 with mergeable priority queues.
(or even $$$O(N)$$$ if we compress equal keys in the priority queue and merge the priority queues in time proportional to the smaller subtree depth)
I think my submission for E works in O(NlogN) using small-to-large merging technique. 268419277
Let diff[node] be difference between a[node] and (summation of a[child]). Each subtree maintains a set of nodes ordered by depth such that diff[node] < 0. On DFS, if diff[currentNode] > 0, take first node in the set, update result and diff[firstNode]. To combine the sets of each child to parent, small-to-large merging is used.
Personally, I like this round very much, not because I get positive delta, but because the problems are really cool. D & E are easy problems but they require you to seek for the solution (that is, I don't get the solution as soon as I read the problem statement). I think that reminds me how to set problems like this.
UPD: It seems that the straight greedy solution to E works well. However I was writing minkowski sum, which seems of more correctness to me.
The model solution for F seems fascinating (thus I'm looking forward to seeing the editorial soon) because my solution works in the same time complexity but is much more complex than yours (as a result, I've made many, many mistakes in some of the details). And I got WA on 3 on G1 during contest time. For now, I've understood why my solution to G1 is wrong through several small hacks. Sorry for being so weak, but I will try to spend more time solving G2 and H.
I wonder whether using min cost max flow was expected to pass in E (268173238)
D can also be solved NlogN by using priority queues
How?
A will take the smallest value possible, B can make changes in the runtime. i.e go back in time and take the best ones using priority queues.
https://codeforces.com/contest/1987/submission/268370561
Waooo...
Can anyone please help me understand why my idea for problem D is not working?
Here is what I am trying to do.
Alice always takes smallest number. Bob takes any number bigger than what alice took which also has the smallest frequency and alice won't be able to reach it.
code: https://codeforces.com/contest/1987/submission/268190399
Bob sometimes may want to eat a less tasty cake with a higher frequency over a cake that has lower frequency but high tastiness.
Could you give example?
Let there be cakes with tastiness 1, 2, 2, 3, 3, 4, 4, 4, 5 Bob will want to eat the cakes with tastiness 3 first.
Thank you so much.
But how does Bob decide which particular cake to eat?
E. Tell me if my approach is correct or not. First, you calculate sum of values of direct children, just below, for every node, lets call it sum[i] for node i. Next we do a dfs traversal. For leaf nodes we do not have to do anything. Then for others nodes, if val[i]>sum[i], then we need to perform some operations. We need to add exactly val[i]-sum[i] to one of the child node, but in doing so you are changing the value of child node, which can result in val[child]>sum[child], and if this happens, you just need to add val[i]-sum[i] again to the child's children node, and so on.
If I am going in the right direction, do tell me. If not, please point out the mistake.
"We need to add exactly val[i]-sum[i] to one of the child node": this is wrong
In this example you add 1 to each node in the second row, total cost 2. If you add 2 to a node, the cost will be 3Example tree:
268472191
can you please help me why am i getting WA, my approach- first calculated the min distance from the node to a leaf node in height vector and in diff vector stored the value a[node]-(sum of a[child])
then for each node , if diff>0 this means that child nodes needs operations to be done,so i check if there is any child node such that its value can be increased without further nodes being affected then for the remaining difference i just multiply the distance stored in height vector Please point out the mistake
I am curious on why a Greedy solution of removing the highest pair for problem F doesn't work. Couldn't find the counterexample during the contest. Example: https://codeforces.com/contest/1987/submission/268216353
1
8
1 1 3 4 1 2 2 1 taking the last pair gives 3 but there is optimal order to erase the whole sequence
Why iterating over the maximum possible cake Bob could remove and choosing the others greedely yields an incorrect answer? serious question
dp-forces
Could somebody explain me, how to solve D using DP, please?
I have used 2D DP. First state is for distinct positions and 2nd state is for Bob's time to eat all cakes of a specific tastiness. Bob will try to eat cakes in ascending order of their tastiness. He should eat all the cakes of a type so that Alice can't eat that type of cake. Bob will have 2 options.
You can see my code for better understanding: https://codeforces.com/contest/1987/submission/268196842
Firstly, it could be seen that the optimal strategy for Alice is to eat cakes in ascending orders of tastiness from the smallest to largest one. So if Bob wants to minimize her overall number of cakes, he must try to eat up all cakes of some particular tastiness in order to avoid Alice eats that type of cakes (I used the term type here instead of tastiness from now on for convenience). So let's get the frequency of each type of cakes and sort those in ascending order of tastiness. Let $$$dp_{i,j}$$$ be the minimum number of cakes that Bob will eat if we consider the first $$$i$$$ types and Bob has been eaten $$$j$$$ types of cake. The transition is pretty simple, but we need to ensure that the number of cakes that Bob eats needs to be smaller or equal to Alice does at any time of the transition. The answer will be the total number of types minus the maximum number types that Bob could eat which can be checked by the valid transitions we made.
Submission: 268186295
Have a look at my explanation in another thread.
Video Editorials
A : https://youtu.be/LeWk-F2aoSA
B : https://youtu.be/OPuPMg2lsek
C : https://youtu.be/zMuZ3Wyd7bk
The problem were very interesting thank you
C was also doable regardless of direction.
The formula for the time taken, assuming the $$$i$$$th column is the bottleneck is: $$$h_i + i$$$ (proof is simple)
So we just try out all $$$i$$$ and get the one that gives the max $$$h_i + i$$$, that would be the real bottleneck.
https://codeforces.com/contest/1987/submission/268234160
Can you please help me prove it.
I should first clarify what I mean by bottleneck. Check out this example for initial heights 1 2 3 5 4:
The fourth flower is the "bottleneck" because it is taller than all the flowers behind it hence nothing from behind will stop it from going down every second (this is only the initial idea, we later explain how index, aka width, comes into play).
Hence, the fourth flower reaches height
1after4seconds.Notice how the previous flower heights will be dragged down along with the fourth column (we ignore after 4):
There's this pattern where when $$$h[4]$$$ ($$$1$$$ indexed) is first $$$0$$$, then $$$h[3]$$$ is $$$1$$$, and so on...
Hence after $$$h[4]$$$ is $$$0$$$ it will take $$$(4 - 1)$$$ seconds for the rest to become $$$0$$$.
When we're $$$0$$$ indexed, the index of the fourth flower is $$$3$$$ anyway. Hence the $$$h_i + i$$$ formula.
Also in case you're wondering, it doesn't matter if the sequence behind is monotonically increasing (the explanation is a bit long but think of the other extreme where it's actually monotonically decreasing before the bottleneck).
Now it's perfectly possible something after the fourth column was the real bottleneck, especially since using this formula we got $$$h_i + i$$$, so there's an aspect of width to it too, not just height, hence why we take the max over the whole array.
Decent explanation!
Can anyone please explain to me why the second loop is used in problem D in the tutorial?
Here's the code: --->
int n = a.size(); vector<int> dp(n + 1, inf); dp[0] = 0; for (int i = 1; i <= n; i++) { vector<int> ndp = dp; for (int k = 1; k <= n; k++) { int nv = dp[k - 1] + a[i - 1]; if (nv <= i - k) { ndp[k] = min(ndp[k], nv); } } dp = ndp; }It would be very helpful if someone could explain it. Thanks in advance! ^-^
Is the example array in problem F’s tutorial wrong? The array is [1,2,5,4,5,7,1,8] ,how can we remove a[7] and a[8] when a[7] != 7?
Thanks, fixed.
Can someone please review my profile and guide me ? I have tried different problems of different ranges(900-1300 more frequently ), but still I am unable to think of even the easiest problems for eg I was unable to think in correct direction for C (which was probably of the range 1100-1200) and took a lot of time for B and came up with a difficult and unnecessary approach compared to other solutions for problem B. Can someone please guide me on how can I improve from my current situation? it would me a lot of help for me Thankyou
I do not personally think C was that easy though it had around 8k submissions, B was easy once you see whats actually happening, i would suggest you to solve codeforces ladders on your own as well as give virtual contest regularly, it would definitely help you grow!
Thankyou Sir, and can you tell me more about Code Forces ladders ?
Google them they are a set of 100 questions for each difficulty ranging from A to F.
In problem C, Ive seen that most have used dp to solve it. Ive spent the past 5 hours to prove that the approach is correct.
I could only prove the following 1987C - Basil's Garden 1. if A[i] > dp[i+1]+1 => dp[i] = A[i]
I was not able to prove the other parts. And Im also wondering how the guys had gotten the idea and were also able to prove this confidently in a decently less quantity of time.
Could someone please help me...
We let dp[i] be the seconds for arr[i] to reach 0. As you have proven, if arr[i] > dp[i+1] or i = n, then dp[i] = arr[i].
So now let's assume arr[i] <= dp[i+1]. We need to prove that this means dp[i] = dp[i+1] + 1.
First off, it's easy to see that dp[i+1] + 1 is a lower bound for dp[i]. In order for arr[i] to reach 0, arr[i+1] needs to have reached 0 too, and two consecutive elements of arr can never both decrease and reach the same value at the same second.
Therefore dp[i] >= dp[i+1] + 1.
Now let's establish that dp[i+1] + 1 is an upperbound for dp[i]. Suppose that it is not, and that dp[i] = dp[i+1] + c, for a constant c > 1. Then, after dp[i+1] seconds, arr[i+1] = 0 and arr[i] = c. That implies that arr[i] and arr[i+1] never got equalized, therefore arr[i] > arr[i+1] should hold. But if arr[i] can keep getting decreased while never getting equalized with arr[i+1], then dp[i] = arr[i] -> dp[i] <= dp[i+1] -> dp[i] < dp[i+1] + 1, and that violates the lowerbound.
Therefore the upperbound is dp[i+1] + 1.
Lowerbound is equal to upperbound, therefore if arr[i] <= dp[i+1], dp[i] = dp[i+1] + 1.
In the problem F I just traversed from the back and whenever I find the element satisfying the condition just delete it and next element and then again traverse from the back again. doing this until we can. Most of the test cases are passing. Can someone please help. My solution 268194520
Try this
1
10
1 1 3 4 1 2 9 9 2 7
The answer is 4:
1 1 3 4 1 2 9 9 2 7
1 1 1 2 9 9 2 7
1 2 9 9 2 7
1 9 2 7
2 7
thank you so much.
so? everybody can provide solution pieces and make it a full solution?
Can someone please review my profile and guide me ? Thank you :-)
The sample input in problem F is kind of weak so that even I mistakenly typed a
<=as a>=, it would pass the sample.I consistently received
Wa On Pretest 2until I realized what a stupid mistake I had made.me too bruh btw the sample is too weak I think, since any kinda algorithm can pass so I got a lot WAs on pretest 2 or 3.
Upsolved G1 with dp:
Since we know that the paths leading up to the root don't collide, we can keep track of 3 dps for each section, where segment i represents all numbers from l_i+1 to r_i-1. We can keep track of longest single path up to p_i, longest sum of lengths of two paths such that the root of the left path has higher p vale, and same thing but with the right path. Then, we can calculate answer by going through all the root positions.
Submission: https://codeforces.com/contest/1987/submission/268250482
Update: it also worked for G2 with some (annoying) changes!
Too much DP.
How can C be solved if height can also be 0? Like test 9 0 9 0 and answer 9. I was wondering that the whole time and then realized the constrains :(
it can be seen that ranges separated by 0 do not affect each others
I spent 30 more minutes just to realize $$$O(n^3)$$$ can pass F2 lmao...
not my best performance but atleast i got the references
Cheating has increased so much . At this point solutions should be leaked intentionally which fails on main test and passes the pretests . This would be good way to catch cheaters which changes the code using AI to avoid plag checks .
OMG, a CrossCode reference! That game was amazing, not nearly well enough known considering how good it is.
I'm very much curious to learn that for problem D, is there any other approach than dp?
See Comment
For those who were not able to understand the DP solution of D. 268157606
can you explain the idea also?
Let Bob greedily eat most types of cakes so that none of those types of cake are left for alice when she reaches there.
By type I mean cakes with unique tastiness values.
Vladithur add this approach for D as well if possible.
good blog
.
Can anyone explain me the dp in problem D how is it working and I am not able to see dp logic generally in problems how can I become better at it ?
someone please explain why my code for problem E is giving wrong answer on testcase 2 below is my submission https://codeforces.com/contest/1987/submission/268323462
Solution of problem D with priority_queue:
https://codeforces.com/contest/1987/submission/268268604
Can someone please help me to understand whats wrong in my B solution?
code: https://codeforces.com/contest/1987/submission/268337048
1 -> put all differences in a ascending order heap
2 -> for each peek, i know i can pick a maximum k equals to heap size, and i can pick it peek times
3 -> sum coins and sum shifts from previous peek to next elements
4 -> Ex:
4 8 16
I know i can choose K = 3, 4 times I'll spend (3 * 4 ) + 4 coins = 16 coins Shift 4 for all next -> 4 12 continue
Whats wrong, pls? X-X Fails here: wrong answer 11th numbers differ — expected: '2020469122', found: '1207241465'
I came up with a solution to G1 during the contest, but it failed on pretest #3. The idea is to build the cartesian tree first, than enumerate the root of the diameter, which seperates it into two parts.
When dealing with root u, first consider if the two parts come from different subtrees, which can be done by calculating the maximum depth in the subtree. It can be proven that going up from v to u on the cartesian tree is the longest way in all possible trees according to the constraints.
Second, consider if the two parts come from the same subtree (for example, the left one). First we set v to the left son of u and keep going to its right son, and pull out the chain (the points on the chain are the only points whose $$$r_v$$$ is u). The diameter we are considering is made by fliping one choice from $$$l_v$$$ to $$$r_v$$$. By enumerating the point that is flipped, we can find the longest route. Since one point will be enumerated only twice, the complexity is $$$O(n)$$$.
(Maybe it is hard to understand and you may have to check the code)
I wonder whether the algorithm itself is right and how to hack it.
Submission
I think the answer should be $$$5$$$.
F%c% your moms a$h0le$
[now down vote]
Can someone recommend similar problem to D but easier, like 1400, 1500
Thank you for the amazing contest
Problem F is so beautiful, I love it. Also how did I miss the Celeste reference in problem H lol
void solve() {
ll n ;
cin>>n ;
vll v(n);
for(int i=0;i<n;i++){ int x ; cin>> x; v[x-1]++; } vll a; for(int i=0;i<n;i++){ if(v[i]!=0) a.pb(v[i]); }
int m=a.size(); vector<vector<ll>> dp(m+1,vector<ll>(m+1,-1)); dp[0][0]=0; for(int i=1;i<m;i++){ for(int j=i;j>0;j--){ dp[i][j]=dp[i-1][j-1]; if(j>=a[i]){ dp[i][j]=max(dp[i-1][j-a[i]]+1,dp[i-1][j-1]); } }}
// for(int i=0;i<m;i++){ // for(int j=0;j<m;j++) // cout<<dp[i][j]<<" "; // cout<<endl ; // }
ll ans=0; for(int i=0;i<m;i++) ans=max(ans,dp[m-1][i]); cout<<m-ans<<endl ;}
can anyone correct this code for D. I cant able to figure it out.
More tasks like D??Thanks
Can someone tell me why my code is not working? I am getting a runtime error in test case 9 https://codeforces.com/contest/1987/submission/268383994
Solution for G1 (440ms & 132MB):
Define
$$$f(\text{int l},\,\text{int r},\,\text{bool lemax},\,\text{bool remax}) = (\text{maximum diameter},\,\text{maximum depth},\,\text{maximum sum of depths of two vertices where one is connected to lemax and one to remax})$$$ if we only consider indices $$$[l,\,r]$$$ and the possible two extra vertices. If $$$\text{lemax} = \text{true}$$$ we also have a vertex to the left that we can connect to, similarly for $$$\texttt{remax}$$$, there's a vertex to the right if it's true. Also note that there's no restriction for the vertices to form a connected graph, because only the maximum must be connected to itself, for all the rest we can reconnect it if we had connected it to itself previously, thus being unconnected wouldn't be a better solution for any of our outputs.
One can easily calculate $$$f(l,\,r,\,\text{lemax},\,\text{remax})$$$ from $$$f(l,\,m-1,\,\text{lemax},\,1)$$$ and $$$f(m+1,\,r,\,1,\,\text{remax})$$$ where m is the index of the maximum element in $$$[l,\,r]$$$. I won't bore you with explanations and different cases that may occur, you can read more in my G1 submission.
Solution for G2 (420ms and 132MB):
Do the same but instead of maximum depth, we output two maximum depths, one for vertices connected to the left and one to the right. Again, the detailed explanations are nothing crazy, but here's my G2 submission.
Overall I loved E and F and liked the rest. They'll be good problems for practicing as well. Thanks very much. Also, this might interest you Vladithur
In G2 the different cases that may occur will handle forced edges.
wanted to point out another similiar dp like recurrence approach.
For G1, my initial idea was to categorize shapes into 3 broad classes : path (self explanatory), hill (2 paths from opposite sides merging at the highest element), skewed_hills (2 paths from same side merging at highest element)
You naturally get left and right skewed hills. This is nearly enough for writing the dp recurrences for G1, except you notice that sometimes a technically invalid skewed_hill can later on be made valid. (for example consider a case like 5 2 1 3 4)
I had to maintain 2 extra variables called skew_right_bad and skew_left_bad respectively. You can check my code for exact details of the recurrences https://codeforces.com/contest/1987/submission/268296892
A similiar approach can be made to work for G2 but it is much cleaner to categorize things by actual properties instead of their shapes.
I needed the following properties :
one_path[dir] = largest path which can be extended in direction dir
two_path[dir1][dir2][max] = largest set of 2 paths where the first path can be extended in direction dir1, second path in direction dir2, and the maximum element is path numbered max.
Submission : https://codeforces.com/contest/1987/submission/268339806
Epic
For problem E I traverse each node and return a list of information in each node
https://codeforces.com/contest/1987/submission/268349130
Really enjoyed solving problem E! It took me a long time to come up with the idea but eventually I figured out I could treat each node as either a "source" or a "sink". Then we must send the difference between parents and their children down to sink nodes, in BFS order to minimize cost. Then it becomes clear that the cost to use a sink node is dist * difference, and we can use the sink node until it is equal to the sum of its children, or infinitely if it is a root.
https://imgur.com/a/FseB4Kt
Can someone explain the formal proof to the claim in Hint 3 of problem E?
it is not less optimal to apply the operation on (v1,w2) and (v2,w1).or why the bottom up approach works in the small-to-large solution?
So how soon can we see the tutorial of problem G & H