I found a small shortage of materials in English on this topic and I want to start with translated article of rationalex:
The problem
We want to learn how to compare root trees for isomorphism (equality up to the renumbering of vertices + the root of one tree necessarily goes to the root of another tree).
Hash of vertex
Note that since we cannot appeal to the vertex numbers, the only information we can operate on is the structure of our tree.
We will consider as a hash of a vertex without children some constant (for example, 179), and for a vertex with children we will use as a hash some function from the sorted list of hashes of children (since we do not know the true order in which the children should go, we need to bring them to the same form). The hash of the root tree will be considered the hash of the root.
By construction, the hashes of isomorphic root trees coincide (the author leaves the proof by induction on the number of levels in the tree to the reader as an exercise).
Polynomial hash is not suitable
Consider 2 trees:
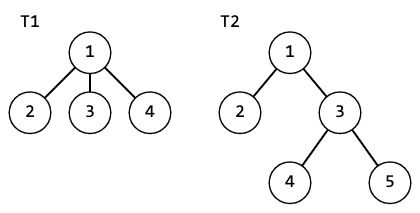
If we calculate for them to take a polynomial hash as a function of children, we get: $$$h(T1)=179+179p+179p^2=179+p(179+179p)=h(T2)$$$
Which hash is suitable?
As a good hash function, for example, this is suitable
For this hash function, it may seem that it is possible not to sort the hashes of children, but this is not the case, because when calculating floating-point numbers, we have an error, and in order for this summation result to be the same for isomorphic trees, it is also necessary to sum the children in the same order.
An example of a more complicated hash function:
Asymptotics
All we need to do at each level is sorting the vertices by hash value and summing, so the final complexity is: $$$O(|V|log(|V|))$$$
I want to continue on my own:
In the reality of Codeforces, these approaches have problems in the form of hacks (which can be seen, for example, by hacks of this task). Therefore, I want to talk about an approach in which there are no collisions.
What is this magic hash function?
Let's sort the hashes of the children for the vertex and match the number to this array, which we will consider the hash of the vertex (if the array is new, then we will assign it the minimum unoccupied number, otherwise we will take the one that has already been given).
Why does it work fast?
It is easy to notice that the total size of the arrays that we counted is $$$n - 1$$$ (each addition is a transition along the edge). Due to this, even using treemap for mapping, all accesses to it will require a total of $$$O(n \cdot log(n))$$$. Comparing a key of size $$$sz$$$ with another key works in $$$O(sz)$$$ and such comparisons for each key will occur $$$O(\log(n))$$$ times, and the sum of all $$$sz$$$, as we remember, is $$$n-1$$$, so it turns out a total of $$$O(n\cdot \log(n))$$$. (You might think that it is worth using hashmap, but this does not improve the asymptotics and causes the probability of a collision).











First of all, what do you call a "polynomial hash"? Is it something like sum of "take $$$i$$$-th child, multiply its hash by $$$p^i$$$"? If it is true, then this "hash" changes when we swap two children with different hashes, which shouldn't happen.
UPD: okay, I wasn't very observant and didn't read the whole paragraph with "hash of subtree is hash of sorted list of smth"
Second, I think that the last way you mentioned is the most popular and simple, but just out of theoretical interest one can read this ancient article by rng_58. It contains two pictures which seem to have expired, but I have the second of them:
I tried the approach mentioned in the rng_r8's blog (Multivariable polynomial hashing) but got wa on test case 7. Did I implement it in the wrong way or did the main case had the hack input for which it would give wa.
submission link
You did something wrong. My solution got AC
Thanks people_plus_plus
I compared my code with yours and changed two things and it got accepted.
Firstly, for all vertex my code did....
hash[vertex] *= (depth[vertex] + hash[child]), but I didn't mutliply the hash of that vertex with its own depth. (I didn't multiply the hash of parent which of course was 0 during that time).
It still gave wa.
Then I used mod in the hash multiplication instead of just purely using unsigned long long which automatically mods any value greater than unsigned long long max with unsigned long long max.
However, In rng's blog, he didn't tell to multiply the hash with depth of that vertex itself.
Also, it would be really helpful if you can tell me what is the reason that using a smaller MOD (1e9 + 9) instead of a larged MOD (unsigned long long) avoided collision. Should I do that every time I use hashing?
Where is a reason why you should not use auto mod like you did in your first submission. Standart types use mod $$$2^x$$$ and it can be easily get collision even on small data! You can read about this here https://codeforces.com/blog/entry/4898?locale=ru
In simple words: dount use automatically mods, use your own mods like $$$10^9 + 7$$$. To be sure, use int64 mods. Be carefull when you use hash on codeforces, because there are hacks. You can avoid being hacked by choose a random prime-mod number.
Did you take any permission to publish my algorithm?
There's a way to hash rooted trees which has a better time complexity and is also easy to implement, whose expected number of collisions doesn't exceed $$$O(\frac{n^2}{2^w})$$$. It is mentioned here.
To avoid being hacked, you can use random parameter instead of 1237123 in the article when solving Codeforces problems.
Can you explain the proof of the expected number of collisions and the meaning of $$$w$$$ in $$$2^w$$$? Thank you.
Polynomial hash works fine, you just need to represent tree's euler tour as a correct bracket sequence —
(when you walk along an edge from parent to child and)when you go backward from child to parent. So T1 will be()()()and T2 will be()(()()). Then hash it as usual string (of course, with sorting childs' hashes).Doesn't it look like it's easier to create a collision with such hashing? (In context of hacks)
Every tree is just a string in such representation. If we use polynomial hashing for strings, why shouldn't we use it in this case?
I solved https://codeforces.com/contest/1800/problem/G using your idea. It's nice
Can anybody suggest some problems on the topic?
UPD:
1800G - Симмеtreeя
763D - Тимофей и плоское дерево
Kattis — Two Charts Become One
I recently solved a problem from an ICPC regionals using this technique: Two Charts Become One
It seems often a good idea to compute not hashes for subtrees, but simply numeric representations $$$val(u)$$$ — consecutive integers from $$$0$$$ and beyond, where $$$u$$$ is the root, which defines a subtree rooted at $$$u$$$. The values $$$val(u)$$$ and $$$val(v)$$$ will be equal if and only if the subtrees with roots $$$u$$$ and $$$v$$$ are equal (or isomorphic).
You can just use
map<vector<int>, int> valsfor memoization. Then if for $$$u$$$ you need to calculate the value of $$$val(u)$$$, then take all children $$$w_1, w_2, \dots, w_k$$$ of $$$u$$$ and make a vector $$$[val(w_1), val(w_2), \dots, val(w_k)]$$$. If it has a value in $$$vals$$$, then take the value from there, if not, enter the next integer (well, just use current $$$vals.size()$$$).And just recursively calculate this for all subtrees. In total, it will work for $$$O(nlogn)$$$, apparently. And no issues with possible hash collisions. You can think of the resulting values as perfect hashes.
Thank you! i literally do not know about hashing at all. i just saw your comment and solved the problem 1800G - Симмеtreeя .
My submission if anyone want :- 195934874
Hey, may you please explain a little more on how this algorithm works? I am not able to understand... Please!
Here's how I understand it, and hopefully it helps you.
We want to assign a number for every node $$$u$$$ (we write this as $$$val(u)$$$) based on the structure of its children (by looking at $$$childrenInfo(u) = [val(w_1), val(w_2), ..., val(w_k)]$$$ where $$$w_1, w_2, \dots, w_k$$$ are children of $$$u$$$). So, two nodes with the same $$$childrenInfo$$$ will have the same value in $$$val$$$ and have the same subtree structure (or isomorphic). For example, in this tree:
The algorithm works like DFS. So to calculate for $$$val(u)$$$, we want to first get $$$childrenInfo(u)$$$. Notice that to get $$$childrenInfo(u)$$$, we have to know $$$val(w_i)$$$ for all of its children $$$w_i$$$ first. So do the DFS like the following code snippet. Note that we use
valsto store/remember what number to assign to $$$val(node)$$$ with certain $$$childrenInfo$$$.Wow, great explanation, understood completely :) Thanks for such a detailed comment.
You are welcome! :)
I believe storing hash values for all the subtrees will lead to $$$O(n^2)$$$ memory complexity. Please correct me if I am wrong.
Upd — nvm i understood how it's $$$O(n)$$$
Does anyone know proof of the complexity of this algorithm?
Proofed in the end of post?
I'm asking about an algorithm Mike presented.
This is the algo I described in the end)
Oh shit you're right, thanks.
I just want to know what should be the most suitable hash function for root tree?
Hash[node]=(product of (Hash[child]+degree(node))*(prime^x)%modwhere x=number of child and mod=1e9+7;Is this working hash??
Relevant problem: https://cses.fi/problemset/task/1700/