Hi everyone!
The 2022-2023 ICPC Latin America Regional Programming Contest was held last weekend. Given that (as far as I know) there is no official editorial for the problems, I decided to create one.
Please notice that, given that these are not the official solutions, there can be typos/mistakes in the explanations. Feedback is always appreciated :)
I would like to thank lsantire for reviewing the editorial and providing valuable feedback.
Don't hesitate to reach out to me if you have any questions/suggestions. Thank you!
Think in which case a person loses money. Remember we can choose the order in which events happen.
Let's fix a person $$$p$$$ and call $$$a$$$ and $$$b$$$ to the people $$$p$$$ will ask for money. It's easy to see that $$$p$$$ loses money if $$$a$$$, $$$b$$$ and $$$p$$$ are asked for money before $$$p$$$ requests $$$a$$$ or $$$b$$$ to pay.
This is equivalent to checking if, starting the process in any person, we can visit the three people without taking into account the edges that start in $$$p$$$. By fixing the starting vertex and performing a BFS/DFS, we can check if this happens. Time complexity to perform this process for all the possible values of $$$p$$$ is $$$\mathcal{O}(n^3)$$$. This is too slow.
To improve our algorithm, we can consider reversing the edges of the graph. Now we need to check if there is a vertex that is reachable from $$$p$$$, $$$a$$$ and $$$b$$$. This means we can run our BFS/DFS starting from $$$a$$$, $$$b$$$ and $$$p$$$, and then check if there is a vertex that was visited by all of them. Given that for a fixed value of $$$p$$$ we only transverse the graph 3 times, the final time complexity is $$$\mathcal{O}(n^2)$$$.
#include <bits/stdc++.h>
#define fst first
#define snd second
#define fore(i,a,b) for(int i=a,ThxDem=b;i<ThxDem;++i)
#define pb push_back
#define ALL(s) s.begin(),s.end()
#define FIN ios_base::sync_with_stdio(0);cin.tie(0);cout.tie(0)
#define SZ(s) int(s.size())
using namespace std;
typedef long long ll;
typedef pair<int,int> ii;
const int MAXN=1010;
vector<int> g[MAXN];
int vis[MAXN],am[MAXN];
void go(int pos, int bad){
vis[pos]=1;
for(auto x:g[pos]) if(x!=bad && !vis[x]) go(x,bad);
}
int main(){FIN;
int n; cin>>n;
vector<ii> v(n);
fore(i,0,n){
int x,y; cin>>x>>y; x--; y--;
v[i]={x,y};
g[x].pb(i); g[y].pb(i);
}
fore(i,0,n){
vector<int> am(n),now={i,v[i].fst,v[i].snd};
for(auto x:now){
memset(vis,0,sizeof(vis));
go(x,i);
fore(j,0,n) am[j]+=vis[j];
}
int can=0;
fore(j,0,n) can|=am[j]==3;
cout<<(can?"Y":"N");
}
cout<<"\n";
}
Look at the problem another side. Try to compute for each token, which is the minimum id of a player that can get it.
Instead of iterating over the players, let's compute for each token, the minimum id of a player that can get it
Let's assume that for a given token, we want to check if there is any player with id in $$$[l,r]$$$ that can get it. If there is at least one valid player in the range, it's easy to see that the one maximizing $$$A_i \cdot X + B_i$$$ will be one of them.
Let's build a segment tree over the players. On each node, we store the lines of all the players with id contained in the node's range. Now, for a given token $$$(X,Y)$$$, we can start descending the tree. Let's assume we are currently standing in one particular node of the tree, and let's call $$$V$$$ to the maximum value of $$$A_i \cdot X + B_i$$$ for this node.
- If $$$Y \geq V$$$, then none of the players in the node's range can take this token. We can ignore all of them.
- If $$$Y < V$$$, we know there is at least one player in this range that will take it. Let's check using recursion if there is at least one in the left child of the node. If we couldn't find it, then move to the right child.
It's easy to see that in each level of the segment tree we visit at most 2 nodes, so we check $$$\mathcal{O}(\log n)$$$ nodes in total.
The only thing remaining is to be able to quickly check the maximum value in one node for a given token. To do that, we can use convex hull trick on each node to be able to answer queries of maximum value of $$$A_i \cdot X + B_i$$$ in $$$\mathcal{O}(\log n)$$$.
Final time complexity: $$$\mathcal{O}(n \cdot \log^2 n)$$$. This can also be improved to $$$\mathcal{O}(n\cdot\log n)$$$ by processing tokens in increasing order of $$$X$$$, but it was not necessary to get AC. Alternatively, you can also use Li Chao tree to solve the problem.
#include <bits/stdc++.h>
#define fst first
#define snd second
#define fore(i,a,b) for(int i=a,ThxDem=b;i<ThxDem;++i)
#define pb push_back
#define ALL(s) s.begin(),s.end()
#define FIN ios_base::sync_with_stdio(0);cin.tie(0);cout.tie(0)
#define SZ(s) int(s.size())
using namespace std;
typedef long long ll;
typedef pair<ll,ll> ii;
typedef ll tc;
struct Line{tc m,h;};
struct CHT {
vector<Line> c;
int pos=0;
tc in(Line a, Line b){
tc x=b.h-a.h,y=a.m-b.m;
return x/y+(x%y?!((x>0)^(y>0)):0);
}
void add(tc m, tc h){
Line l=(Line){m,h};
if(c.size()&&m==c.back().m){
l.h=min(h,c.back().h);c.pop_back();if(pos)pos--;
}
while(c.size()>1&&in(c.back(),l)<=in(c[c.size()-2],c.back())){
c.pop_back();if(pos)pos--;
}
c.pb(l);
}
inline bool fbin(tc x, int m){return in(c[m],c[m+1])>x;}
tc eval(tc x){
while(pos>0&&fbin(x,pos-1))pos--;
while(pos<c.size()-1&&!fbin(x,pos))pos++;
return c[pos].m*x+c[pos].h;
}
};
struct STree{
vector<CHT> st;int n;
STree(int n): st(4*n+5), n(n) {}
void upd(int k, int s, int e, int p, ii now){
st[k].add(-now.fst,-now.snd);
if(s+1==e)return;
int m=(s+e)/2;
if(p<m) upd(2*k,s,m,p,now);
else upd(2*k+1,m,e,p,now);
}
int get(int k, int s, int e, ii val){
if(val.snd >= -st[k].eval(val.fst)) return -1;
if(s+1==e) return s;
int m=(s+e)/2;
int ans=get(2*k,s,m,val);
if(ans<0) ans=get(2*k+1,m,e,val);
return ans;
}
void upd(int p, ii now){upd(1,0,n,p,now);}
int get(ii val){return get(1,0,n,val);}
};
int main(){FIN;
int n; cin>>n;
vector<pair<ii,int>> a(n);
fore(i,0,n) cin>>a[i].fst.fst>>a[i].fst.snd,a[i].snd=i;
int q; cin>>q;
vector<pair<ii,int>> qs(q);
fore(i,0,q) cin>>qs[i].fst.fst>>qs[i].fst.snd,qs[i].snd=i;
sort(ALL(a)); sort(ALL(qs));
STree st(q);
fore(i,0,q) st.upd(qs[i].snd,qs[i].fst);
vector<vector<int>> ans(q);
fore(i,0,n){
int now=st.get(a[i].fst);
if(now!=-1) ans[now].pb(a[i].snd);
}
fore(i,0,q){
int k=SZ(ans[i]);
sort(ALL(ans[i]));
ans[i].insert(ans[i].begin(),k-1);
fore(j,0,SZ(ans[i]))cout<<ans[i][j]+1<<" \n"[j+1==SZ(ans[i])];
}
}
Look at the process in the reverse order. What happens if $$$H$$$ is in the left/right half of the list?
Let's consider the process backwards (i.e. starting from the last fold).
If $$$H$$$ is in the upper half of the paper, then in the previous step, it was in the half that was folded on top of the other one. Otherwise, it was on the other part. By using this observation we can compute, for each step, if we should fold or not the part in which $$$H$$$ is.
Now let's start the process from the beginning from $$$P$$$. Now we have some cases:
- If in this moment the position should be part of the half that will be folded, then if $$$P$$$ is in the left half we push $$$L$$$ to the answer, or $$$R$$$ otherwise.
- On the contrary, if it shouldn't be on the folded half, we push $$$R$$$ if $$$P$$$ is in the left half, or "L" otherwise.
Don't forget that whenever we fold one part on top of the other, the order of its elements is reversed.
#include <bits/stdc++.h>
#define fst first
#define snd second
#define fore(i,a,b) for(int i=a,ThxDem=b;i<ThxDem;++i)
#define pb push_back
#define ALL(s) s.begin(),s.end()
#define FIN ios_base::sync_with_stdio(0);cin.tie(0);cout.tie(0)
#define SZ(s) int(s.size())
using namespace std;
typedef long long ll;
typedef pair<int,int> ii;
int main(){FIN;
ll n,p,h; cin>>n>>p>>h; p--; h--;
vector<int> w;
string ans;
for(int k=n-1;k>=0;k--){
w.pb(h>=(1ll<<k));
if(w.back()) h=(1ll<<(k+1))-1-h;
}
for(int k=n-1;k>=0;k--){
if(w[k]){
if(p<(1ll<<k)){
ans.pb('L');
p=(1ll<<k)-1-p;
}
else{
ans.pb('R');
p=(1ll<<(k+1))-1-p;
}
}
else{
if(p<(1ll<<k)){
ans.pb('R');
}
else{
ans.pb('L');
p-=1ll<<k;
}
}
}
cout<<ans<<"\n";
}
Just simulate what you are asked for! :)
This was the easiest problem in the contest. The solution is to simulate the process described in the statement. It can be done in several ways.
#include <bits/stdc++.h>
#define fst first
#define snd second
#define fore(i,a,b) for(int i=a,ThxDem=b;i<ThxDem;++i)
#define pb push_back
#define ALL(s) s.begin(),s.end()
#define FIN ios_base::sync_with_stdio(0);cin.tie(0);cout.tie(0)
#define SZ(s) int(s.size())
using namespace std;
typedef long long ll;
typedef pair<int,int> ii;
int main(){FIN;
int n,x,y; cin>>n>>x>>y;
fore(i,0,n){
char a,b; cin>>a>>b;
if(a=='Y' || !y) cout<<"Y ", y++, x--;
else cout<<"N ";
if(b=='Y' || !x) cout<<"Y\n", x++, y--;
else cout<<"N\n";
}
}
Is the answer big? Think about possible cases. Or even better, maybe there is a way to avoid having to consider tricky cases.
This problem has many solutions.
It can be proven that the answer is at most 3. This allows us to solve it in $$$\mathcal{O}(1)$$$ by some annoying case analysis, or even in $$$\mathcal{O}(n^2)$$$ by brute force with some observations.
Let me introduce a different solution that doesn't require any case analysis. We will solve the problem by using dynamic programming. In particular, $$$f(i,a,b)$$$ denotes if we can cover two squares of sizes $$$1\times a$$$ and $$$1\times b$$$ respectively, if we only have tiles of sizes $$$1\times 1, 1\times 2, \ldots, 1\times i$$$.
If $$$a = 0$$$ and $$$b = 0$$$, then $$$f(i,a,b)=\it{true}$$$.
We can skip the tile of size $$$1\times i$$$, transitioning to $$$f(i-1,a,b)$$$.
If $$$i \neq k$$$, we can try to use the tile of size $$$1\times i$$$ to cover either the first square ($$$f(i-1,a-i,b)$$$) or the second one ($$$f(i-1,a,b-i)$$$). Be careful to check that $$$i\leq a$$$ and $$$i\leq b$$$ respectively.
The solution then is to iterate over the values of $$$a$$$ and $$$b$$$ such that $$$a$$$ is at most the size of the first part, and $$$b$$$ is at most the size of the second part. If $$$f(n,a,b) = \it{true}$$$, then we can cover $$$k+a+b$$$ squares. By taking the maximum value we can obtain over all possible values of $$$a$$$ and $$$b$$$ (denote it by $$$v$$$), we can note that the answer is $$$n-v$$$.
The number of states in our dp is $$$\mathcal{O}(n^3)$$$. In order to save some memory, we can notice that $$$f(i,a,b)$$$ only have transitions to $$$f(i-1,x,y)$$$ for some values of $$$x$$$ and $$$y$$$. We can keep the dp values only for the previous value of $$$i$$$. By doing this, we reduce memory usage to $$$\mathcal{O}(n^2)$$$.
This looks too slow. But we can notice that $$$a+b<=n$$$, so the total amount of states is actually at most $$$\frac{n^3}{4}$$$. This is fast enough for $$$n\leq 1000$$$.
#include <bits/stdc++.h>
#define fst first
#define snd second
#define fore(i,a,b) for(int i=a,ThxDem=b;i<ThxDem;++i)
#define pb push_back
#define ALL(s) s.begin(),s.end()
#define FIN ios_base::sync_with_stdio(0);cin.tie(0);cout.tie(0)
#define SZ(s) int(s.size())
using namespace std;
typedef long long ll;
typedef pair<int,int> ii;
const int MAXN=1010;
bool dp[MAXN][MAXN];
int main(){FIN;
int n,k,e; cin>>n>>k>>e;
int l=e, r=n-k-e;
dp[0][0]=1;
fore(len,1,n+1) if(len!=k){
for(int i=l;i>=0;i--) for(int j=r;j>=0;j--){
if(len<=i) dp[i][j]|=dp[i-len][j];
if(len<=j) dp[i][j]|=dp[i][j-len];
}
}
int ans=k;
fore(i,0,l+1) fore(j,0,r+1) if(dp[i][j]){
ans=max(ans, i+j+k);
}
cout<<n-ans<<"\n";
}
If we fix the root of the first tree, we can try to solve it recursively.
Let's assume the root of $$$T_2$$$ is always vertex $$$1$$$. We are going to iterate over the root $$$R$$$ of $$$T_1$$$, and we will assume it is matched with the root of $$$T_2$$$.
Now we need to solve the problem for rooted trees, assuming that the root of both trees will always be included. In particular, let's denote as $$$f(i,j)$$$ as a boolean value that denotes if we can remove some nodes of the subtree of $$$i$$$ in $$$T_1$$$, so that the remaining nodes form a tree that is isomorphic to the subtree of $$$j$$$ in $$$T_2$$$. We want to find out the value of $$$f(R,1)$$$.
We are going to denote the set of children of vertex $$$i$$$ in $$$T_1$$$ as $$$\operatorname{ch_1}(i)$$$. In the same way, we define $$$\operatorname{ch_2}(i)$$$ to represent children of $$$i$$$ in $$$T_2$$$. Let's see how to compute $$$f(i,j)$$$.
Let's create a bipartite graph, where the left part is $$$\operatorname{ch_1}(i)$$$ and the right one is $$$\operatorname{ch_2}(j)$$$. Given $$$x \in \operatorname{ch_1}(i)$$$ and $$$y \in \operatorname{ch_2}(j)$$$, we add an edge between $$$x$$$ and $$$y$$$ if $$$f(x,y) = \it{true}$$$ (we check this value with recursion). Notice that we reduced the problem to finding a maximum matching. If we can match every vertex of the right part, then $$$f(i,j) = \it{true}$$$. To compute this, we can use Hopcroft-Karp's algorithm.
Let's analyze the time complexity of our solution. Notice that if we fix two nodes $$$v_1$$$ and $$$v_2$$$ in $$$T_1$$$ and $$$T_2$$$ respectively, we will add one edge to the bipartite graph while computing $$$f(i,j)$$$ only when $$$i$$$ is the parent of $$$v_1$$$ and $$$j$$$ is the parent of $$$v_2$$$ (and this happens at most once for a fixed root). This means that the total edges in all the matchings required to compute $$$f(R,1)$$$ is $$$\mathcal{O}(n^2)$$$.
The time complexity of running Hopcroft-Karp's algorithm is $$$\mathcal{O}(m\cdot \sqrt{n})$$$, where $$$m$$$ is the amount of edges. In our case, $$$m = n^2$$$, so the cost of computing $$$f(R,1)$$$ for a fixed value of $$$R$$$ is $$$\mathcal{O}(n^2\cdot \sqrt{n})$$$. Given that we iterate over all the possible values of $$$R$$$, we conclude that the final complexity of our solution is $$$\mathcal{O}(n^3\cdot \sqrt{n})$$$, which clearly fits in the time limit.
#include <bits/stdc++.h>
#define fst first
#define snd second
#define fore(i,a,b) for(int i=a,ThxDem=b;i<ThxDem;++i)
#define pb push_back
#define ALL(s) s.begin(),s.end()
#define FIN ios_base::sync_with_stdio(0);cin.tie(0);cout.tie(0)
#define SZ(s) int(s.size())
using namespace std;
typedef long long ll;
typedef pair<int,int> ii;
const int MAXN=110;
vector<int> g1[MAXN],g2[MAXN];
struct Matching{
vector<vector<int>> g;
vector<int> mt,mt2,ds;
int n,m;
Matching(int n, int m):n(n),m(m),mt2(n),mt(m),ds(n),g(n){}
bool bfs(){
queue<int> q;
fill(ALL(ds),-1);
fore(i,0,n)if(mt2[i]<0)ds[i]=0,q.push(i);
bool r=false;
while(!q.empty()){
int x=q.front();q.pop();
for(int y:g[x]){
if(mt[y]>=0&&ds[mt[y]]<0)ds[mt[y]]=ds[x]+1,q.push(mt[y]);
else if(mt[y]<0)r=true;
}
}
return r;
}
bool dfs(int x){
for(int y:g[x])if(mt[y]<0||ds[mt[y]]==ds[x]+1&&dfs(mt[y])){
mt[y]=x;mt2[x]=y;
return true;
}
ds[x]=1<<30;
return false;
}
int mm(){
int r=0;
fill(ALL(mt),-1); fill(ALL(mt2),-1);
while(bfs()){
fore(i,0,n)if(mt2[i]<0)r+=dfs(i);
}
return r;
}
};
int dp[MAXN][MAXN];
int solve(int me, int he, int pme=-1, int phe=-1){
int &r=dp[me][he];
if(r>=0)return r;
r=0;
int chme=SZ(g1[me])-(pme>=0);
int chhe=SZ(g2[he])-(phe>=0);
if(chhe==0){
r=1;
}
else if(chme>=chhe){
Matching mt(SZ(g1[me]), SZ(g2[he]));
fore(i,0,SZ(g1[me])) if(g1[me][i]!=pme){
fore(j,0,SZ(g2[he])) if(g2[he][j]!=phe){
if(solve(g1[me][i],g2[he][j],me,he)){
mt.g[i].pb(j);
}
}
}
int tot=mt.mm();
r=tot==chhe;
}
return r;
}
int main(){FIN;
int n; cin>>n;
fore(i,1,n){
int x,y; cin>>x>>y; x--; y--;
g1[x].pb(y); g1[y].pb(x);
}
int m; cin>>m;
fore(i,1,m){
int x,y; cin>>x>>y; x--; y--;
g2[x].pb(y); g2[y].pb(x);
}
fore(i,0,n){
memset(dp,-1,sizeof(dp));
if(solve(i,0))cout<<"Y\n",exit(0);
}
cout<<"N\n";
}
104252G - Gravitational Wave Detector
Write down the different equations for a fixed minor plant. Try to get something in terms of points belonging to the polygons.
Let's denote the two polygons as $$$P$$$ and $$$Q$$$ respectively. We will solve the case in which the middle point coincides with a minor plant. The other two cases can be handled in a really similar way.
Let's consider a particular minor plant $$$c$$$, the answer is $$$Y$$$ if there exists two points $$$a \in P$$$ and $$$b \in Q$$$, such that:
\begin{equation} \frac{a + b}{2} = c \end{equation}
We can rewrite this as: \begin{equation} (a + b) = 2*c \end{equation}
Given that $$$P$$$ and $$$Q$$$ are convex, the points that can be represented as a sum of $$$a \in P$$$ and $$$b \in Q$$$ also form a convex polygon with $$$\mathcal{O}(n+m)$$$ vertices, and we can construct it in linear time. This is called the Minkowski sum of $$$P$$$ and $$$Q$$$.
So, after computing the Minkowski sum of $$$P$$$ and $$$Q$$$, we have reduced the problem to be able to check if $$$c$$$ lies inside a convex polygon. This can be done with binary search in $$$\mathcal{O}(\log n)$$$.
Final time complexity of the solution is $$$\mathcal(n+q\cdot \log n).$$$
#include <bits/stdc++.h>
#define fst first
#define snd second
#define fore(i,a,b) for(int i=a,ThxDem=b;i<ThxDem;++i)
#define pb push_back
#define ALL(s) s.begin(),s.end()
#define FIN ios_base::sync_with_stdio(0);cin.tie(0);cout.tie(0)
#define SZ(s) int(s.size())
using namespace std;
typedef long long ll;
typedef pair<int,int> ii;
struct pt{
ll x,y;
pt(){}
pt(ll x, ll y):x(x),y(y){}
pt operator +(pt p){return pt(x+p.x,y+p.y);}
pt operator -(pt p){return pt(x-p.x,y-p.y);}
pt operator *(ll k){return pt(x*k,y*k);}
pt operator /(ll k){return pt(x/k,y/k);}
ll operator %(pt p){return x*p.y-y*p.x;}
bool left(pt p, pt q){return (q-p)%(*this-p)>=0;}
bool left2(pt p, pt q){return (q-p)%(*this-p)>0;}
bool operator <(pt p){return x<p.x||(x==p.x&&y<p.y);}
};
void normalize(vector<pt> &p){
int n=SZ(p);
if(p[2].left2(p[0],p[1]))reverse(ALL(p));
int pi=min_element(p.begin(),p.end())-p.begin();
vector<pt> s(n);
fore(i,0,n)s[i]=p[(pi+i)%n];
p.swap(s);
}
vector<pt> chull(vector<pt> p){
if(SZ(p)<3)return p;
vector<pt> r;
sort(ALL(p));
fore(i,0,SZ(p)){
while(SZ(r)>=2&&r.back().left(r[SZ(r)-2],p[i]))r.pop_back();
r.pb(p[i]);
}
r.pop_back();
int k=SZ(r);
for(int i=SZ(p)-1;i>=0;i--){
while(SZ(r)>=k+2&&r.back().left(r[SZ(r)-2],p[i])) r.pop_back();
r.pb(p[i]);
}
r.pop_back();
normalize(r);
return r;
}
bool haslog(vector<pt> &p, pt q){
if(q.left2(p[0],p[1])||q.left2(p.back(),p[0]))return 0;
int a=1,b=p.size()-1;
while(b-a>1){
int c=(a+b)/2;
if(!q.left2(p[0],p[c]))a=c;
else b=c;
}
return !q.left2(p[a],p[a+1]);
}
vector<pt> minkowski_sum(vector<pt> p, vector<pt> q){
int n=SZ(p),m=SZ(q),x=0,y=0;
fore(i,0,n) if(p[i]<p[x]) x=i;
fore(i,0,m) if(q[i]<q[y]) y=i;
vector<pt> ans={p[x]+q[y]};
fore(it,1,n+m){
pt a=p[(x+1)%n]+q[y];
pt b=p[x]+q[(y+1)%m];
if(b.left(ans.back(),a)) ans.pb(b), y=(y+1)%m;
else ans.pb(a), x=(x+1)%n;
}
return ans;
}
vector<pt> operator *(vector<pt> v, ll x){
for(auto &a:v) a=a*x;
return v;
}
int main(){FIN;
int n; cin>>n;
vector<pt> p(n);
fore(i,0,n) cin>>p[i].x>>p[i].y;
reverse(ALL(p));
int m; cin>>m;
vector<pt> q(m);
fore(i,0,m) cin>>q[i].x>>q[i].y;
reverse(ALL(q));
vector<pt> me=minkowski_sum(p,q);
vector<pt> he=minkowski_sum(p*2,q*-1);
vector<pt> he2=minkowski_sum(q*2,p*-1);
me=chull(me);
he=chull(he);
he2=chull(he2);
int k; cin>>k;
fore(i,0,k){
pt p; cin>>p.x>>p.y;
if(haslog(me,p*2) || haslog(he,p) || haslog(he2,p))cout<<"Y";
else cout<<"N";
}
cout<<"\n";
}
Each small race imposes some conditions for each player about where it can/can't be located. Try to compute these positions for each of them.
Let's analyse the $$$\it{i}$$$-th small race:
- If the $$$\it{j}$$$-th horse took part of it, it means it's final place should be at least $$$W_i$$$.
- If the $$$\it{j}$$$-th horse didn't take part of it, it's final place can't be exactly $$$W_i$$$.
By considering these conditions, we can compute for each horse, which are the valid positions for it in the answer. After we do this, we can construct a bipartite graph where left part represents horses and right part represents positions. We add an edge between $$$i$$$ and $$$j$$$ if the $$$\it{i}$$$-th horse can be placed in the $$$\it{j}$$$-th position.
It's easy to see that we need to find a perfect matching in this graph. Given that $$$N\leq 300$$$, any of the well known matching algorithms will fit in the time limit.
#include <bits/stdc++.h>
#define fst first
#define snd second
#define fore(i,a,b) for(int i=a,ThxDem=b;i<ThxDem;++i)
#define pb push_back
#define ALL(s) s.begin(),s.end()
#define FIN ios_base::sync_with_stdio(0);cin.tie(0);cout.tie(0)
#define SZ(s) int(s.size())
using namespace std;
typedef long long ll;
typedef pair<int,int> ii;
const int MAXN=310;
vector<int> g[MAXN];
int mat[MAXN];bool vis[MAXN];
int match(int x){
if(vis[x])return 0;
vis[x]=1;
for(int y:g[x])if(mat[y]<0||match(mat[y])){mat[y]=x;return 1;}
return 0;
}
void max_matching(int n){
vector<ii> r;
memset(mat,-1,sizeof(mat));
fore(i,0,n)memset(vis,0,sizeof(vis)),match(i);
}
int main(){FIN;
int n; cin>>n;
map<string,int> mp;
vector<string> v(n);
fore(i,0,n) cin>>v[i], mp[v[i]]=i;
vector<int> mn(n);
vector<vector<int>> can(n,vector<int>(n,1));
int q; cin>>q;
vector<int> wh(n);
while(q--){
int k,low; cin>>k>>low; low--;
fore(i,0,n) wh[i]=0;
fore(i,0,k){
string s; cin>>s;
int x=mp[s];
mn[x]=max(mn[x],low);
wh[x]=1;
}
fore(i,0,n) if(!wh[i]) can[i][low]=0;
}
fore(i,0,n) fore(j,0,n) if(j<mn[i])can[i][j]=0;
fore(i,0,n) fore(j,0,n) if(can[i][j]) g[i].pb(j);
max_matching(n);
vector<int> ans(n,-1);
fore(i,0,n) if(mat[i]>=0) ans[i]=mat[i];
fore(i,0,n)cout<<v[ans[i]]<<" \n"[i+1==n];
}
104252I - Italian Calzone & Pasta Corner
Fix the starting dish and act greedily :)
Let's iterate over the first dish we take. We can maintain a set of the dishes that can be visited in the next step (i.e. neighbours of visited cells). From all of the candidates in the set, it's always better to take the smallest one. We repeat this procedure until we run out of candidates. The cost of doing this process for a starting dish is $$$\mathcal{O}(n^2\cdot \log n)$$$.
Given that we iterate over $$$\mathcal{O}(n^2)$$$ starting cells, the total complexity is $$$\mathcal{O}(n^4\cdot \log n)$$$. If the solution is coded without a big constant factor, you can make it fit in the time limit.
In order to optimize our approach, let's iterate the starting dish in increasing order of value. We can notice that if we visited a cell when we executed the process in a previous candidate, it's useless to start all over again with this value as the starting position: during that previous step, we visited all the positions we would visit now, plus some others too (so, the answer was bigger).
Although this optimization improves the performance of the algorithm, it doesn't actually improves its time complexity. There are cases in which it will perform $$$\mathcal{O}(n^4\cdot \log n)$$$ operations, but the constant factor is smaller (and for $$$n\leq 100$$$ it runs fast enough).
For anyone that got curious, here is a case I was able to find while discussing the complexity with lsantire.
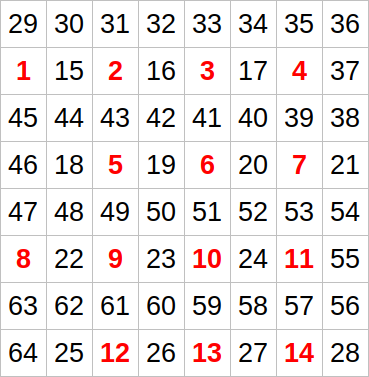
It's easy to see that all the red numbers will be tested as starting points, and each of them will do the "zig zag" over the entire grid. The total number of times we visit cells during the process is somewhere around $$$\frac{n^4}{16}$$$.
If I set $$$n=500$$$ with this case, it takes almost one minute for my code to finish.
#include <bits/stdc++.h>
#define fst first
#define snd second
#define fore(i,a,b) for(int i=a,ThxDem=b;i<ThxDem;++i)
#define pb push_back
#define ALL(s) s.begin(),s.end()
#define FIN ios_base::sync_with_stdio(0);cin.tie(0);cout.tie(0)
#define SZ(s) int(s.size())
using namespace std;
typedef long long ll;
typedef pair<int,int> ii;
const int MAXN=110;
int p[MAXN*MAXN];
int find(int x){return p[x]=p[x]==x?x:find(p[x]);}
void join(int x, int y){p[find(x)]=find(y);}
vector<ii> mov={{1,0},{0,1},{-1,0},{0,-1}};
int a[MAXN][MAXN],pingo[MAXN],vis[MAXN*MAXN];
ii pos[MAXN*MAXN];
int main(){FIN;
int n,m; cin>>n>>m;
vector<pair<int,ii>> v;
fore(i,0,n) fore(j,0,m) cin>>a[i][j],a[i][j]--,pos[a[i][j]]={i,j};
fore(i,0,n*m) p[i]=i;
int ans=0;
vector<int> asd(n*m);
fore(i,0,n*m) if(!asd[i]){
fore(j,0,n*m) vis[j]=0;
priority_queue<int,vector<int>,greater<int>> q;
q.push(i);
vis[i]=1;
int res=0;
while(SZ(q)){
int now=q.top(); q.pop();
asd[now]=1;
int x=pos[now].fst, y=pos[now].snd;
res++;
for(auto dir:mov){
int nx=x+dir.fst, ny=y+dir.snd;
if(nx<0||ny<0||nx==n||ny==m||a[nx][ny]<a[x][y]||vis[a[nx][ny]])continue;
vis[a[nx][ny]]=1;
q.push(a[nx][ny]);
}
}
ans=max(ans,res);
}
cout<<ans<<"\n";
}
Runners and queries can be seen as line equations. It may be useful to iterate the photos in some particular order that can help us compute things in an easier way.
Let's first think about how to detect which photos are trash.
We can rewrite the equation of the position of the $$$\it{i}$$$-th runner as $$$S_i*t - T_i\cdot S_i$$$. This is the equation of a line, which we will denote as $$$f_i$$$, and we will denote as $$$f_i(v)$$$ as the result of evaluating the the $$$\it{i}$$$-th line in $$$t=v$$$.
For a given photo, if we sort all the runners by the value of $$$f_i(U)$$$, we can check if there exists an index $$$j$$$ such that $$$A \leq f_j(U) \leq B$$$ by using binary search. There is a problem: we clearly can't sort all the lines for each photo. Instead, we will process the photos in increasing order of $$$U$$$, while keeping the sorted list of runners in the meantime.
Let's take two lines $$$f_i$$$ and $$$f_j$$$ such that $$$S_i > S_j$$$. We will denote the value of $$$t$$$ such that $$$f_i(t) = f_j(t)$$$ as $$$x_{i,j}$$$. It's not hard to see that for every value $$$U \in (-\infty, x_{i,j}]$$$, the $$$\it{i}$$$-th runner will be before the $$$\it{j}$$$-th one in the sorted list of lines. If we consider that $$$U \in (x_{i,j},\infty)$$$, then the relative order between them should be swapped.
Initially, we can sort the lines assuming that $$$U=-\infty$$$. We will maintain in a set the values of $$$x_{i,j}$$$ for the lines $$$i$$$ and $$$j$$$ that are located in consecutive positions in the current list. Now, let's start processing the photos by increasing value of $$$U$$$. When processing a new photo, we should swap consecutive lines such while $$$x_{i,j} \leq U$$$ (and update the corresponding values of the affected positions in the set). After we finish updating all the necessary positions, it's easy to see that now the lines are sorted by the value of $$$f_i(U)$$$, so we can apply the binary search we mentioned before.
We can notice that when two consecutive values $$$i$$$ and $$$j$$$ are swapped, we will never swap them again, so the amount of times we do a swap is $$$\mathcal{O}(n^2)$$$. This means that the complexity of computing the photos that are trash is $$$\mathcal{O}((n^2+m)\cdot \log n)$$$. Let's remove from the list all the photos that are not trash, since they won't affect any query.
Now let's process the queries offline. Instead of counting the amount of trash photos for each query, we will compute for which queries each photo is trash.
It turns out we can use the exact same algorithm to keep the sorted array of queries by the current value of $$$U$$$ while iterating over the photos again. After updating the order of queries for a given photo, we need to add one to the value of all the queries such that $$$f_i(U) < A$$$ or $$$f_i(U) > B$$$. Given that the queries are ordered by $$$f_i(U)$$$, all the positions in which we add one are located in a prefix or a suffix of the list.
We need a data structure that allows us to perform two operations:
- Swap two consecutive positions.
- Add one to a range of positions.
There are several ways to do this. For example, you can use treap, a lazy segment tree or even a Fenwick tree.
The final complexity of the solution is $$$\mathcal{O}((n^2+q^2+m)\cdot \log n)$$$.
#include <bits/stdc++.h>
#define fst first
#define snd second
#define fore(i,a,b) for(int i=a,ThxDem=b;i<ThxDem;++i)
#define pb push_back
#define ALL(s) s.begin(),s.end()
#define FIN ios_base::sync_with_stdio(0);cin.tie(0);cout.tie(0)
#define SZ(s) int(s.size())
using namespace std;
typedef long long ll;
typedef pair<ll,ll> ii;
struct STree {
vector<ii> st; vector<int> lazy;int n;
STree(int n): st(4*n+5), lazy(4*n+5,0), n(n) {}
void push(int k, int s, int e){
if(!lazy[k])return;
if(s+1==e) st[k].fst+=lazy[k];
if(s+1<e){
lazy[2*k]+=lazy[k];
lazy[2*k+1]+=lazy[k];
}
lazy[k]=0;
}
void put(int k, int s, int e, int p, ii v){
push(k,s,e);
if(s+1==e){st[k]=v;return;}
int m=(s+e)/2;
if(p<m) put(2*k,s,m,p,v);
else put(2*k+1,m,e,p,v);
}
void upd(int k, int s, int e, int a, int b, int v){
push(k,s,e);
if(s>=b||e<=a)return;
if(s>=a&&e<=b){
lazy[k]+=v;
push(k,s,e);return;
}
int m=(s+e)/2;
upd(2*k,s,m,a,b,v);upd(2*k+1,m,e,a,b,v);
}
ii get(int k, int s, int e, int p){
push(k,s,e);
if(s+1==e) return st[k];
int m=(s+e)/2;
if(p<m) return get(2*k,s,m,p);
return get(2*k+1,m,e,p);
}
void upd(int a, int b, int v){upd(1,0,n,a,b,v);}
void put(int a, ii b){put(1,0,n,a,b);}
ii get(int a){return get(1,0,n,a);}
};
ll INF=1e18+10;
ll eval(ii a, ll x){
return x*a.fst+a.snd;
}
ll get(ii x, ii y){
if(x.fst==y.fst) return x.snd<=y.snd ? INF : -INF;
if(x.fst<y.fst) return INF;
ll a=x.fst, b=x.snd, c=y.fst, d=y.snd;
ll ans=(d-b)/(a-c)-1;
while(eval(x,ans) <= eval(y,ans)) ans++;
return ans;
}
const int MAXN=1010;
ii v[MAXN];
int ans[MAXN];
int cmp(int i, int j){
ii x=v[i], y=v[j];
return x.fst==y.fst?x.snd<y.snd:x.fst>y.fst;
}
vector<pair<ii,int>> doit(vector<pair<ii,int>> a, int n, int flag){
sort(ALL(a));
int m=SZ(a);
vector<int> id(n);
fore(i,0,n) id[i]=i;
sort(ALL(id),cmp);
STree st(n);
fore(i,0,n) st.put(i,{0,id[i]});
set<ii> s;
fore(i,0,n-1){
ll now=get(v[id[i]],v[id[i+1]]);
if(now!=INF) s.insert({now,i});
}
vector<pair<ii,int>> aa;
for(auto x:a){
while(SZ(s) && s.begin()->fst<=x.fst.fst){
int i=s.begin()->snd;
fore(it,i-1,i+2) if(it>=0&&it+1<n){
ll x=get(v[id[it]],v[id[it+1]]);
if(x!=INF) s.erase({x,it});
}
//swap i with i+1
ii v1=st.get(i), v2=st.get(i+1);
st.put(i,v2); st.put(i+1,v1);
swap(id[i],id[i+1]);
fore(it,i-1,i+2) if(it>=0&&it+1<n){
ll x=get(v[id[it]],v[id[it+1]]);
if(x!=INF) s.insert({x,it});
}
}
int stt,en;
{
int l=0,r=n-1;
while(l<=r){
int m=(l+r)/2;
if(eval(v[id[m]],x.fst.fst)<x.fst.snd) l=m+1;
else r=m-1;
}
stt=l;
}
{
int l=0,r=n-1;
while(l<=r){
int m=(l+r)/2;
if(eval(v[id[m]],x.fst.fst)<=x.snd) l=m+1;
else r=m-1;
}
en=r;
}
if(stt>en){
st.upd(0,n,1);
aa.pb(x);
}
else{
st.upd(0,stt,1);
st.upd(en+1,n,1);
}
}
fore(i,0,n){
ii now=st.get(i);
ans[now.snd]=now.fst;
}
return aa;
}
int main(){FIN;
int n; cin>>n;
fore(i,0,n) cin>>v[i].fst>>v[i].snd, v[i]={v[i].snd,-v[i].fst*v[i].snd};
int m; cin>>m;
vector<pair<ii,int>> a(m);
fore(i,0,m) cin>>a[i].fst.fst>>a[i].fst.snd>>a[i].snd;
a=doit(a,n,0);
int q; cin>>q;
fore(i,0,q) cin>>v[i].fst>>v[i].snd, v[i]={v[i].snd,-v[i].fst*v[i].snd};
doit(a,q,1);
fore(i,0,q)cout<<ans[i]<<"\n";
}
The amount of times we use the machine isn't too big. We can show that the minimum possible amount is actually achievable.
This problem probably has many different solutions. I'm going to describe the approach I used.
First, let's notice that if we use the machine $$$n$$$ times, we can have at most $$$2^n$$$ different different types of pieces. So we know that the value of $$$n$$$ has to be at least $$$\lceil{\log_2 k}\rceil$$$. Let's show that we can actually achieve this.
First, if $$$k=1$$$, just print $$$0$$$. Otherwise, let's fill the first column and the first row with all the $$$n$$$ colors. Now we have 2 different types, so we can subtract 2 from the value of $$$k$$$.
Given that $$$k \leq 4000$$$, notice that $$$n \leq 12$$$. Also, notice that $$$2^{\frac{n}{2}} \leq 100$$$. Let's denote $$$k_1 = \lfloor \frac{n}{2} \rfloor$$$ and $$$k_2 = \lceil \frac{n}{2} \rceil$$$.
For each value $$$i \in [0,k_1)$$$, iterate over all the rows from $$$2$$$ to $$$100$$$, and if the id of the current row has the $$$i$$$-th bit set, add the color $$$i$$$ to the entire row. You can do the same with columns for the other $$$k_2$$$ values, but using columns instead of rows.
It's not hard to notice that by doing this, we generate exactly $$$2^n$$$ different types of pieces. Also, thanks to the fact that we used every color in each of the cells of the first row and column, every color forms a connected component. So this solution is correct.
The only remaining part is to make the amount of different types exactly equal to $$$k$$$. This can be done in several ways. For example, you can perform the described process only until you detect that you already have $$$k$$$ types, or you can generate all the $$$2^n$$$ types and then clear some cells until the amount is reduced to exactly $$$k$$$.
Time complexity is $$$\mathcal{O}(k)$$$.
#include <bits/stdc++.h>
#define fst first
#define snd second
#define fore(i,a,b) for(int i=a,ThxDem=b;i<ThxDem;++i)
#define pb push_back
#define ALL(s) s.begin(),s.end()
#define FIN ios_base::sync_with_stdio(0);cin.tie(0);cout.tie(0)
#define SZ(s) int(s.size())
using namespace std;
typedef long long ll;
typedef pair<int,int> ii;
const int MAXN=100, K=12;
int ans[MAXN][MAXN],am[1<<K],total,k,tot;
vector<ii> res[MAXN*MAXN];
void print_ans(){
fore(x,0,tot) fore(i,0,MAXN) fore(j,0,MAXN) if(ans[i][j]&(1<<x)){
res[x].pb({i,j});
}
cout<<tot<<"\n";
fore(i,0,tot){
vector<int> to={SZ(res[i])};
for(auto x:res[i]) to.pb(x.fst+1), to.pb(x.snd+1);
fore(i,0,SZ(to))cout<<to[i]<<" \n"[i+1==SZ(to)];
}
exit(0);
}
void rem(int val){
total-=am[val]==1;
am[val]--;
}
void add(int val){
total+=am[val]==0;
am[val]++;
if(total==k) print_ans();
}
int main(){FIN;
cin>>k;
int pw=1;
while(pw<k) pw*=2,tot++;
int n=tot/2, m=(tot+1)/2;
if(k==1){
cout<<"0\n";
exit(0);
}
total=1;
am[0]=MAXN*MAXN;
//first row and column
fore(x,0,tot) fore(i,0,MAXN) fore(j,0,MAXN) if(!i||!j){
rem(ans[i][j]);
ans[i][j]|=1<<x;
add(ans[i][j]);
}
//rows
fore(x,0,n) fore(i,1,MAXN) fore(j,1,MAXN) if(i&(1<<x)){
rem(ans[i][j]);
ans[i][j]|=1<<x;
add(ans[i][j]);
}
//columns
fore(x,0,m) fore(i,1,MAXN) fore(j,1,MAXN) if(j&(1<<x)){
rem(ans[i][j]);
ans[i][j]|=1<<(n+x);
add(ans[i][j]);
}
}
Think greedily. Is there a case in which it's better to type less characters than the ones we can while executing an instruction?
It can be proven that when performing an instruction, it's always optimal to print the maximal amount of letters possible. I will show how to compute this value. During the explanation, $$$\operatorname{lcp}(i,j)$$$ is the length of the longest common prefix between the suffixes of $$$T$$$ that start in $$$i$$$ and $$$j$$$ respectively.
Let's denote the next position to be printed by the machine by $$$i$$$. We will iterate over all possible lengths (between $$$1$$$ and $$$D$$$) of the string that the machine will use now. If the length we are considering now is $$$k$$$, we will be able to write $$$k+\operatorname{lcp}(i,i+k)$$$ letters with this operation.
The value of $$$\operatorname{lcp}(i,i+k)$$$ can be calculated in several ways in $$$\mathcal{O}(\log n)$$$ or $$$\mathcal{O}(1)$$$ (for example, hashing or suffix array), so the time complexity is represented by the amount of times we compute $$$\operatorname{lcp}(i,i+k)$$$ for some values of $$$i$$$ and $$$k$$$.
At first glance, it looks like our algorithm's complexity is $$$\mathcal{O}(n\cdot D)$$$, which would be too slow, but it turns out this is not true. When we compute the maximum value for a starting position, we perform $$$D$$$ calls to the function $$$\operatorname{lcp}$$$, but the key fact is to realize that this value we get is at least $$$D$$$. This means that after doing $$$D$$$ calls, the value of $$$i$$$ will increase by at least $$$D$$$.
This observation makes us conclude that the final complexity is $$$\mathcal{O}(n)$$$ or $$$\mathcal{O}(n\cdot \log n)$$$, depending on how you compute $$$\operatorname{lcp}$$$.
#include <bits/stdc++.h>
#define fst first
#define snd second
#define fore(i,a,b) for(int i=a,ThxDem=b;i<ThxDem;++i)
#define pb push_back
#define ALL(s) s.begin(),s.end()
#define FIN ios_base::sync_with_stdio(0);cin.tie(0);cout.tie(0)
#define SZ(s) int(s.size())
using namespace std;
typedef long long ll;
typedef pair<int,int> ii;
#define RB(x) (x<n?r[x]:0)
void csort(vector<int>& sa, vector<int>& r, int k){
int n=sa.size();
vector<int> f(max(255,n),0),t(n);
fore(i,0,n)f[RB(i+k)]++;
int sum=0;
fore(i,0,max(255,n))f[i]=(sum+=f[i])-f[i];
fore(i,0,n)t[f[RB(sa[i]+k)]++]=sa[i];
sa=t;
}
vector<int> constructSA(string& s){
int n=s.size(),rank;
vector<int> sa(n),r(n),t(n);
fore(i,0,n)sa[i]=i,r[i]=s[i];
for(int k=1;k<n;k*=2){
csort(sa,r,k);csort(sa,r,0);
t[sa[0]]=rank=0;
fore(i,1,n){
if(r[sa[i]]!=r[sa[i-1]]||RB(sa[i]+k)!=RB(sa[i-1]+k))rank++;
t[sa[i]]=rank;
}
r=t;
if(r[sa[n-1]]==n-1)break;
}
return sa;
}
vector<int> computeLCP(string& s, vector<int>& sa){
int n=s.size(),L=0;
vector<int> lcp(n),plcp(n),phi(n);
phi[sa[0]]=-1;
fore(i,1,n)phi[sa[i]]=sa[i-1];
fore(i,0,n){
if(phi[i]<0){plcp[i]=0;continue;}
while(s[i+L]==s[phi[i]+L])L++;
plcp[i]=L;
L=max(L-1,0);
}
fore(i,0,n)lcp[i]=plcp[sa[i]];
return lcp;
}
const int K=18;
int pw[1<<K],st[K][1<<K];
int get(int l, int r){
if(l>r)swap(l,r);
int k=pw[r-l+1];
return min(st[k][l],st[k][r-(1<<k)+1]);
}
int main(){FIN;
string s; cin>>s;
int n=SZ(s),d; cin>>d;
s.pb('a'-1);
auto sa=constructSA(s);
auto lc=computeLCP(s,sa);
sa.erase(sa.begin());
lc.erase(lc.begin());
s.pop_back();
vector<int> rev=sa;
fore(i,0,SZ(sa)) rev[sa[i]]=i;
fore(i,0,SZ(lc)) st[0][i]=lc[i];
fore(k,1,K) fore(i,0,SZ(lc)){
st[k][i]=st[k-1][i];
if(i+(1<<(k-1))<SZ(lc)) st[k][i]=min(st[k][i],st[k-1][i+(1<<(k-1))]);
}
int p=1,v=0;
fore(i,1,1<<K){
if(p*2<=i) p*=2,v++;
pw[i]=v;
}
int pos=0,ans=0;
while(pos<n){
int mx=d;
fore(i,1,d+1) if(pos+i<n){
int x=rev[pos], y=rev[pos+i];
if(x>y)swap(x,y);
int now=get(x+1,y);
mx=max(mx, i+get(x+1,y));
}
ans++;
pos+=mx;
}
cout<<ans<<"\n";
}
Try to think how to represent the state of the nut, and check if you can reach a state that represents being in the final row.
This problem can be solved by performing a BFS/DFS. Let's define which are going to be our states.
Given that rotating the nut horizontally $$$C$$$ times is the same as not rotating it at all, we can represent the current state with two values: the row of the screw where the nut is located, and how many times we rotated the nut horizontally (between $$$0$$$ and $$$C-1$$$). Notice that the amount of states is $$$R\cdot C$$$, and this is at most $$$10^5$$$.
We can start the BFS/DFS from all valid positions in the first row at the same time, and check if we can reach any position in the last row by performing the operations described in the statement.
Checking if a state is valid can be done in several ways, but the easiest one is to iterate each position of the nut naively, because the constraints allow us to do that. Time complexity is $$$\mathcal{O}(R\cdot C^2)$$$.
Don't forget to also try to reverse the string $$$S$$$ and try the BFS/DFS again (representing the flip operation).
#include <bits/stdc++.h>
#define fst first
#define snd second
#define fore(i,a,b) for(int i=a,ThxDem=b;i<ThxDem;++i)
#define pb push_back
#define ALL(s) s.begin(),s.end()
#define FIN ios_base::sync_with_stdio(0);cin.tie(0);cout.tie(0)
#define SZ(s) int(s.size())
using namespace std;
typedef long long ll;
typedef pair<int,int> ii;
int can[1010][110],vis[1010][110];
int main(){FIN;
int n,m; cin>>n>>m;
string s; cin>>s;
vector<string> v(n);
fore(i,0,n) cin>>v[i];
fore(it,0,2){
memset(can,0,sizeof(can));
memset(vis,0,sizeof(vis));
fore(i,0,n) fore(j,0,m){
can[i][j]=1;
fore(k,0,m) if(s[(j+k)%m]=='1') can[i][j]&=v[i][k]=='0';
}
queue<ii> q;
fore(i,0,m) if(can[0][i]) q.push({0,i}),vis[0][i]=1;
while(SZ(q)){
int x=q.front().fst, y=q.front().snd; q.pop();
//horizontal
fore(i,-1,2){
if(can[x][(y+i+m)%m] && !vis[x][(y+i+m)%m]){
q.push({x,(y+i+m)%m});
vis[x][(y+i+m)%m]=1;
}
}
//vertical
if(x&&can[x-1][y]&&!vis[x-1][y]){
q.push({x-1,y});
vis[x-1][y]=1;
}
if(x+1<n&&can[x+1][y]&&!vis[x+1][y]){
q.push({x+1,y});
vis[x+1][y]=1;
}
}
int asd=0;
fore(i,0,m)asd|=vis[n-1][i];
if(asd){
cout<<"Y\n";
exit(0);
}
reverse(ALL(s));
}
cout<<"N\n";
}











Thank u for the hint-solution style!
Good editorial! Some comments on a few of the easier problems:
104252C - City Folding
If you do only R folds, you can notice the element in height $$$H$$$ (0-indexed) is the representation of $$$\frac{H}{2}$$$ in binary, reversed. You don't need to notice this to solve the original problem, but you can get a neat simple description of what the entire final permutation looks like (it's essentially a bit-reversal permutation).
104252I - Italian Calzone & Pasta Corner
You don't need the $$$O(\log n)$$$ term in the complexity, because you can just iterate from $$$1$$$ to $$$RC$$$ and check if the next number is a candidate for expansion or not.
104252K - Kind Baker
Make a 50-pronged fork with all colors you are going to use (like this Ш, but with 50 vertical lines). Now all other squares are connected to this fork, so you can paint them however you like, and there are more than 4000 of them. So number the squares from $$$1$$$ to $$$K-2$$$ and paint square $$$i$$$ with $$$i$$$ in binary.
104252L - Lazy Printing
From my dislike of hashing and wish to avoid copying suffix array: You can also find the longest prefix that is periodic with period $$$P \leq D$$$ via a direct application of KMP.
About problem I: in practice, I think the solution I proposed is faster because, in the worst case I could come up with, the amount of operations is around $$$\frac{n^4}{16}$$$. Even for values of n like 200 or 250, my code finishes in less than a second.
Anyways, I found your solution way simpler to code, and the constant factor is almost non existing. Good call!
I'm usually not very interested in constant optimizations, but if that's the subject another thing you can do in problem I is to use bitsets (if you add edges from smaller numbers to bigger numbers you can treat it is a "count reachable nodes in a DAG" problem, a problem I apparently helped turn into a meme).
Can you elaborate more about how L can be done using kmp?
It is pretty direct as I said: if the KMP failure function is $$$T_i$$$, then the period of the prefix with length $$$i$$$ is $$$i - T_i$$$.
Assuming you know how KMP works, it should be simple to explain why; if you don't, well, I probably shouldn't write an entire KMP tutorial in a comment. :)
104252I — Italian Calzone & Pasta Corner
There is a faster solution which runs in $$$O(n^4)$$$. From each cell, instead of running a priority queue, we can run a simple DFS. Suppose that we are in a certain cell, we will always move to another cell which has a greater value than the current cell we are. When we finish visiting all possible cells, it can be shown that the greedy path mentioned by MarcosK exists.
104252B - Board Game has even another solution :)
You can notice that given a token, you can find the player that takes it by just adding the lines one by one until one line covers the token.
However, it's also possible to take a slower approach using binary search. In each step, just test if any of the first $$$p$$$ lines covers the token by adding the first $$$p$$$ lines to the structure. This procedure would take $$$O(P \cdot log^2 P)$$$.
You may be wondering why we would want to take this approach as repeating this procedure for each token would result in TLE. However, the good part is that you can run all the binary searches in parallel! That would lead to an $$$ O(logP \cdot (P + T \cdot logP)) $$$ solution.
Implementation: 198648853
Another even crazier solution:
Instead of doing a new lichao tree in every iteration of the parallel binary search, you can alternatively make a persistent lichao tree, then for every point you can binary search to find up to what line the condition holds.
Implementation
some hint to solve the problem E in O(1)?
In how many ways can a number x be formed by the sum of two non-negative different integers?
can't thank you enough for this editorial, I love you S2
Hello, will you also upload this year's ICPC problems?
The problems are already uploaded on gym: https://codeforces.com/gym/104736/standings
Thank you, when can I see the solutions sent?