Hi all, my friend asked me a question few months ago.
Problem Statement
Given a tree with $$$N$$$ vertices ($$$v_1, ..., v_N$$$), among them, there is a source vertex $$$v_S$$$ and a destination vertex $$$v_E$$$ ($$$S \ne E$$$, $$$1 \le S,E \le N$$$). Each edge has an integer weight (can be negative, zero, or positive).
Alice starts at $$$v_S$$$ with an initial health value of $$$h$$$, and she wants to reach $$$v_E$$$. When she traverses through an edge with weight $$$w$$$, the weight $$$w$$$ is added to her health value. At any point in time, her health value cannot be negative. After an edge is used, the weight of the edge becomes $$$0$$$. Alice can use the same edge multiple times, but only the first time will affect her health value because the weight of the edge becomes $$$0$$$.
Find out whether Alice can reach $$$v_E$$$ with a non-negative health value.
Constraint
$$$2 \le N \le 2 \times 10^5$$$ (for reference only, the expected solution's complexity needs to be better than $$$O(N^2)$$$)
Example
Example 1
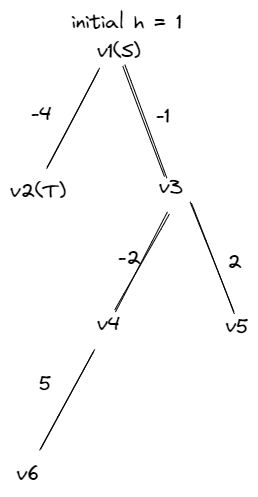
To show why using the same edge multiple times is necessary, consider the following cases (using a degenerated tree for simplicity): $$$S = 3, E = 4, h = 1$$$
$$$v_1$$$ ---(2)--- $$$v_2$$$ ---(-1)--- $$$v_3$$$ ---(-2)--- $$$v_4$$$
The only path for Alice is $$$v_3 \to v_2 \to v_1 \to v_2 \to v_3 \to v_4$$$. Her health value will be $$$1 \to 0 \to 2 \to 2\to 2 \to 0$$$.
Example 2










What about the constraints?
My friend mentioned the optimal solution is better than $$$O(N^2)$$$
Updated: added the constaint
Update: The solution is completely wrong because I forget the problem is on tree.
I think I have come up with a solution.
First you can find out all the connected block in the graph that only have positive edges, and then see all the points in a connected block as a whole point, it's obvious that once you enter a point, then you can increase your health by all the values in this connected block.
So this inspire us to caculate the lowest value to reduce from the destination to get to the every connected block.
Also, merge the connected blocks greedyly, if merge this two connected blocks brings positive health, then merge them, and check whether you can reach the destionations every time you merge a block.
I think the merge part can be obtained by using a prority_queue
Sorry for my poor English, hope you can understand.
After the merge process, how do you find the answer?
merge process is start at the source point's connected block, so we just need to storage the minimum value from destinations to the block that we have merged, and check this value with the health we have now.
During merging, do we only add positive edges into the connected block?
oh i think i have made some mistake, let me think more clearly.
Sorry
Oh I forget it's a tree.
Sorry for my blind-like behaves.
It's ok, no worries haha
A similar problem 1734D - Slime Escape
1734D is only a line instead of tree. Actually this problem is trivial if the tree degenerated to a star and $$$v_S$$$ is on the center of the star (line is a special case of star).
I have a basic idea.
let the health now you have be $$$H$$$.
run a bfs first from the source point and rebuild the tree, in the new graph, every edge has the positive value but it has a limits which means an edge can be formed as $$$(u,v,w,l)$$$, you can gain $$$w$$$ health if $$$H \geq l$$$.
After rebuilding the graph, expand the connected block from source point by greedy.
If you can not expand any more, then you can just run the simulation from the closest point to the destinations and check.
The complexity is $$$\mathcal{O}(n^2)$$$, you can storage all the points you could expand with a priority_queue, and check whether the limitation is reached and then expand.
now the complexity is $$$\mathcal{O}(n \log n)$$$.
How do you construct the new tree?
For example, this testcase:
Oh I made a mistake again, there might be some edges sharing the same the inner node.
The important part of problem M from this contest https://codeforces.com/blog/entry/115769 solves your problem in O(NlogN). It's a shame that the editorials aren't being published directly in the cf posts but you can find both the statement and the editorial here: https://qoj.ac/contest/1221
Thank you very much!
maybe that greedy is not the important part of that problem anyway.
and two problems have an vital difference because in this problem a node is not neccesary to be visit.
If you root at the starting point, then there's a path to the ending and branches to subtrees. Then it's a matter of using the max you can use from those subtrees, but you're right to say that the problems are different although you can use that problem's solution to solve this one by only merging things to the main path if they give positive contribution.
An easier solution:
this dfs returns what you can squeeze out of a subtree. Call this on the hanging subtrees and use those that end up with positive value after considering the edge above it. In fact, this solution can be modified to solve (start, end) queries in O(logN) or maybe even better.
What does the (start, end) queries refer to?
It means that queries would specify the source and destination, instead of them being fixed.
Will the dfs code works for following case?
h = 0
E——(-100)——S——(-5)——v1——(200)——v2
The right subtree of S contributes 195 to the bestBalance. But it is actually impossible to reach v2 because of the edge with weight of -5
Did I miss anything?
Sorry, I misread the statement when I said that. "At any point in time, her health value cannot be negative" I read that the opposite.
I'm pretty sure that we can solve it with the first idea that I mentioned as I described. In the problem that I linked using an edge would first bring your HP down then you gain HP, which works with the condition of maintaining HP as non-negative.
It'd look something like: root the tree at S. Start at S. When at a vertex, unlock the hanging subtrees (as in subtrees that don't belong to the S-E path). Unlocking means pushing their "compression" events into a heap to solve it like the editorial that I mentioned. When you get some event that wants to merge with the main path, then merge it if it ends up gaining you total HP and the "lose hp first" part doesn't send you to negative hp. Otherwise, break this process (keep the heap as is because you might be able to merge the event later) and try to move on to the next vertex in the S-E path. If you're able to reach E then the answer is yes.
I think this works because actually we're only interested in events where vertices actually gain total HP. For those events, the exchange argument is that we merge the ones that lose the least hp first. I'm not completely sure how to prove this more or less formally since I've been introduced to this greedy algorithm only recently, so maybe someone can jump in here to help me.
In the editorial:
I am not quite sure what does the optimal order obtained, and how do we merge the parent with children? For example, do we merge v1 and v2 in the example above?
Besides, in the editorial, it mention that there will be $$$2^{(m−n+1)}$$$ trees, but is this number correct when a same vertex haves more than 2 incoming edges?
For example, four vertex (1,2,3,4) and five edges(1-2, 2-3, 3-4, 1-4, 2-4). $$$2^{(m−n+1)} = 2^{(5-4+1)} = 4$$$, but we only have 3 trees:
The 2^(m-n+1) part isn't important to this blog but you're right to say it's not always that. The editorial's point for that is that 2^(m-n+1) is the worst case.
The optimal order is obtained by applying the exchange argument in the same way as we would in an array. Then it's the same as problems like https://codeforces.com/problemset/gymProblem/102916/K and many others that have used this idea. I'm pretty sure Errichto's video about exchange argument has a problem exactly like that but in an array as well.
Thanks for the explanation but I am still a bit unsure about the merging process, since the problem provided looks very different from this case. Is it possible to write a pseudocode?
Besides, will that solution works on the following testcase?
The possible path is v1-v3-v5-v7-v5-v3-v1-v2
Yes.
luanmenglei also read this. In order to optimize the merges, we have vertices ordered by priority of merging in a heap. The priority is the same as the bloodseeker problem that I linked. When merging, we unite both vertices using DSU. A connected component's representant will be the one with lower height, so the one that's above every other one in the same component. After merging, we have to remove the current merge event from the parent in the heap and reinsert it with correct priority.
In order to know the time when we could not expand edges not in the S-T path is: we simply keep the current HP, merge stuff that's outside of S-T path always except when it's being merged into the S-T path and merging it would lose enough HP to send us to negatives or it doesn't profit hp. After merging things into the S-T path, update the HP.
About merges, if we say that a tuple (L, G) is (Loss of HP, Gain of HP), then merging (L1, G1) into (L2, G2) ends up with (min(L2, G2+L1+L2), G2+G1+L1+L2) since we're merging something that comes after into something. For the priority, simply refer to the bloodseeker problem or Errichto's video in this timestamp https://youtu.be/7hFWrKa6yRM?t=1500
I guess you mean (min(L2, L2+G2-L1), G2+G1)?
Do you already have the merging priority in mind? It seems like your approach will always merge from leaf to root?
I meant min(L2, L2+G2+L1), G2+G1+L1+L2), nicely spotted.
I already linked a video talking about the priority, I won't say anything more about that.
Now I see that that solution is wrong anyway. I don't see how to fix it anymore. The block idea that luanmenglei mentioned works by using exchange argument with small to large merging of subtree stuff. It's how I solved IOI19JOBS (warmup problem) when someone asked me about that problem and I'm sure that it works for this problem but it's tricky and I don't feel like explaining it in detail right now right now. The idea is simply to summarize a subtree by having blocks of vertices that you will take all at once and merging blocks if the root block is worse than the next block. You can also create this block structure with the idea from the editorial that I mentioned, but as I said I don't know that idea that well.
Hi tfg, really thank you for sharing all of the resources and sharing! I already watched the youtube video :D
Do you mind to point out why that solution is wrong (maybe share a testcase)?
Wait, it might not be wrong. I got confused because there are 2 ways of summarizing stuff: (L, G) as I explained and (loss of HP you need to pay to enter here, total profit) as in (L, G+L) if L is negative.
Also, after the merge we have actually (min(L2, L2 + G2 + L1), G2+G1+L1+L2 — min(L2, L2 + G2 + L1))) because I forgot that I usually use L being <= 0.
I'm back to thinking this solution works :| it's just that the merge itself is a bit confusing if you don't think about it carefully.
For the (min(L2, L2 + G2 + L1), G2+G1+L1+L2 — min(L2, L2 + G2 + L1)))
The first part is loss of HP to enter the vertex The second part is profit + loss of HP after enter the vertex
So, the final HP after entering the vertex = original HP + first part + second part.
Is that correct?
I have an idea to construct the counter example for this merging approach but I am not too sure. Without knowing the ordering priority, its hard for me to test it. The high level idea is to find a scenario such that all leafs having higher priority than others and they will merge to an internal node, but that causes the first part (loss of HP) of that internal node becomes too big (too negative). Instead we might don’t want to merge some leafs into that internal node. Not sure whether this works..
Something like:
When things profit total HP, the priority is by order of loss of HP. Losing less HP means higher priority. So after merging (-1, 0) and (-2, 5), we'll have (-3, 5) (I'm sure it's this, maybe the formula that I sent ealier might be wrong) and that has higher priority than (-6, 10) and (-20, 100).
But (-1,0) does not profit, it is unsure that whether its subtree will profit before u finish the processing of its whole subtree. In this case, the subtree makes it profit in the end
But (-2, 5) that does profit is merged into the (-1, 0), making it profit. (-2, 5) has higher priority than (-1, 0).
I'm pretty sure the merging idea works, too -- the way I think about it is that you're creating an equivalent tree satisfying the following properties:
Now when processing node v, if the reward is already positive, there is nothing to do.
If the reward is negative, we want to check what is the lowest possible value of requiredHP[v] that we need to make the reward positive by exploring some of the subtree (if the reward can't be made positive, delete this subtree, it's useless). I'm not going to prove this formally either but you can argue that the best strategy is visiting the nodes in the subtree in order of requiredHP, and you can merge those to v to maintain the first invariant. To maintain the second invariant, merge all descendants with requiredHP[d] <= requiredHP[v] to v.
Having the equivalent tree, the original problem is easy as you just take side-paths as long as you can (since all rewards are positive).
Isn’t this just the absolute value of the negative value $$$w$$$ itself?
not every vertices are required to visit, so this greedy have some issues.
just as the testcase below: Imgur the source point is 1, destination is 4
The greedy that I described works for that case. I suggest you to read it word by word again and again.
Oh sorry for i haven't read your latest comment.
Your idea is same as my idea which I told to practice080 in the talk section (we're using the native language), but the process seems to be $$$\mathcal{O}(n^2)$$$, how do you optimise it or i misread something?
More clearly, how to know the time when we could not expand edges not in the S-T path anymore
Should we output the answer for each vertex to each vertex? or the input consists only of N,S,E?
Only for S to E, the output will be a single boolean
Maybe you should collect as much health as possible, return to the source node, and then go to the end node and see if you end up with a positive number?
No