Hello everyone! We're very sorry for the delay >_<
We hope you enjoyed the tasks! Sorry for too tight limits in C so that Java solutions don't pass (actually one of our authors nickname used to be "java." :D), we'll hopefully do a better job next time! Feel free to leave your feedback in the comments.
1867A — green_gold_dog, array and permutation
Author: green_gold_dog
Let's subtract $$$n$$$ from the minimum number, subtract $$$n - 1$$$ from the second minimum, $$$n - 2$$$ from the third $$$\ldots$$$, and subtract $$$1$$$ from the maximum. Then the number of distinct elements will be $$$n$$$. Obviously, it is impossible to achieve a better result.
Let's prove that the number of distinct elements will be equal to $$$n$$$. Suppose $$$c_i = c_j$$$, then without loss of generality, let's say that $$$b_i > b_j$$$, then $$$a_i \leq a_j$$$, which means $$$c_i = a_i - b_i$$$ < $$$a_j - b_j = c_j$$$. Contradiction.
Time Complexity: $$$O(n \log n)$$$ per test case.
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
void solve() {
ll n;
cin >> n;
vector<pair<ll, ll>> arr(n);
for (ll i = 0; i < n; i++) {
ll x;
cin >> x;
arr[i].first = x;
arr[i].second = i;
}
vector<ll> ans(n);
sort(arr.begin(), arr.end());
reverse(arr.begin(),arr.end());
for (ll i = 0; i < n; i++) {
ans[arr[i].second] = i + 1;
}
for (auto i : ans) {
cout << i << ' ';
}
cout << '\n';
}
int main() {
ios_base::sync_with_stdio(false);
cin.tie(0);
cout.tie(0);
ll t = 1;
cin >> t;
for (ll i = 0; i < t; i++) {
solve();
}
}
Author: ace5
Firstly, a string is a palindrome if and only if for any $$$i$$$ ($$$1 \leq i \leq n$$$) $$$s_i = s_{n-i+1}$$$ (because when reversed, $$$s_i$$$ becomes $$$s_{n-i+1}$$$).
We can divide the characters into pairs, where each pair consists of $$$s_i$$$ and $$$s_{n-i+1}$$$. If $$$s_i = s_{n-i+1}$$$, then we need to have $$$l_i = l_{n-i+1}$$$ in order to obtain equal elements after XOR. Therefore, either $$$l_i = l_{n-i+1} = 0$$$ (with $$$0$$$ ones) or $$$l_i = l_{n-i+1} = 1$$$ (with $$$2$$$ ones). If $$$s_i \neq s_{n-i+1}$$$, then $$$l_i \neq l_{n-i+1}$$$ must hold ($$$1$$$ one in any case). Additionally, if $$$n$$$ is odd, then $$$l_{n/2+1}$$$ can be either $$$0$$$ or $$$1$$$ (with $$$0$$$ or $$$1$$$ ones).
We can iterate over the number of pairs where $$$l_i = l_{n-i+1}$$$ will have two ones, as well as whether there will be a one in the center or not. This way, we can obtain all possible numbers of ones in $$$l$$$, i.e., all good $$$i$$$.
Time Complexity: $$$O(n)$$$ per test case.
#include <bits/stdc++.h>
using namespace std;
int main()
{
ios_base::sync_with_stdio(false);
cin.tie(0);
int t;
cin >> t;
while(t--)
{
int n;
cin >> n;
string s;
cin >> s;
string t(n+1,'0');
int ans = 0;
int max_1 = 0;
int max_2 = 0;
for(int i = 0;i <= n/2-1;++i)
{
if(s[i] == s[n-i-1])
max_2++;
else
ans++;
}
if(n%2 == 1)
max_1++;
for(int j = 0;j <= max_2;++j)
{
for(int k = 0;k <= max_1;++k)
{
t[ans + j*2 + k] = '1';
}
}
cout << t << "\n";
}
}
1867C-Salyg1n and the MEX Game
Author: salyg1n
The correct strategy for Alice is to add the number $$$\operatorname{MEX}(S)$$$ to the set $$$S$$$ on the first move, and add the last removed number on the remaining moves.
Let m = $$$\operatorname{MEX}(S \cup {\operatorname{MEX}(S)})$$$, at the start of the game. In other words, m is equal to the second $$$\operatorname{MEX}$$$ of the set $$$S$$$. $$$m \geq 1$$$.
Notice that after the first move, $$$\operatorname{MEX}(S) = m$$$, and no matter what Bob removes, we will return that number to the set, so the result of the game will always be equal to $$$m$$$.
Let's prove that with Bob's optimal play, we cannot achieve a result greater than m.
Notice that the $$$\operatorname{MEX}$$$ of a set is the largest number k such that all numbers from $$$0$$$ to $$$k-1$$$ inclusive are present in the set.
Let $$$p_i$$$ be the number of numbers from $$$0$$$ to $$$i-1$$$ inclusive that appear in the set $$$S$$$. Then $$$\operatorname{MEX}(S)$$$ is equal to the maximum $$$i$$$ such that $$$p_i = i$$$.
If Bob removes the number $$$y$$$ during his turn, he decreases all values $$$p_i$$$ where $$$i > y$$$ by $$$1$$$. So, if $$$y = \operatorname{min}(S)$$$, Bob decreases all non-zero values $$$p_i$$$ by $$$1$$$.
Alice can increase some values $$$p_i$$$ by $$$1$$$ during her turn. Therefore, after Alice's first move, $$$\operatorname{MEX}(S)$$$ will no longer increase if Bob keeps removing the minimum, because no non-zero values of $$$p_i$$$ will increase (Bob decreases them by $$$1$$$, and Alice increases them by at most $$$1$$$).
It is obvious that in order to maximize $$$\operatorname{MEX}(S)$$$ after the first move, Alice needs to add the number $$$\operatorname{MEX}(S)$$$ to the set $$$S$$$.
We have proven that $$$R \leq m$$$ and provided a strategy that achieves a result of $$$m$$$.
Time Complexity: $$$O(n)$$$ per test case.
#include <iostream>
#include <vector>
using namespace std;
void solve() {
int n;
cin >> n;
vector<int> s(n);
for (int i = 0; i < n; ++i)
cin >> s[i];
int mex = -1;
for (int i = 0; i < n; ++i) {
if (i == 0 && s[i] != 0) {
mex = 0;
break;
}
if (i > 0 && s[i] != s[i - 1] + 1) {
mex = s[i - 1] + 1;
break;
}
}
if (mex == -1)
mex = s[n - 1] + 1;
cout << mex << endl;
int y;
cin >> y;
while (y != -1) {
cout << y << endl;
cin >> y;
}
}
int main() {
int t;
cin >> t;
while (t--)
solve();
return 0;
}
Author: ace5
If $$$k = 1$$$, then we can change $$$b_i$$$ to $$$i$$$, so the answer is YES only if $$$b_i = i$$$, otherwise the answer is NO.
Otherwise, let's build an undirected graph with $$$n$$$ vertices and edges ($$$i, b_i$$$). Any component of this graph will look like a cycle (possibly of size $$$1$$$) to each vertex of which a tree is attached (possibly empty).
Let's assume that there are $$$x$$$ vertices in a component, then there are also $$$x$$$ edges in it (since each vertex has exactly one outgoing edge). We can construct a depth-first search (DFS) tree for this component, which will have $$$x - 1$$$ edges. Now, when we add the remaining edge ($$$u, v$$$), a cycle is formed in the component (formed by the edge ($$$u, v$$$) and the path between $$$u$$$ and $$$v$$$ in the DFS tree). Each vertex will have a tree attached to it, because before adding the edge, we had a tree.
Now it is claimed that if the cycle in each component has a size exactly $$$k$$$, then the answer is YES, otherwise NO.
Let's first consider the situation where the size of the cycle in some component is not $$$k$$$. Let the cycle contain vertices $$$v_1, v_2, \cdots, v_x$$$ in that order. Now let's look at the last operation in which one of the $$$l_i$$$ was equal to some element from the cycle. If the size of the cycle is less than $$$k$$$, then in the last operation there will be at least one vertex not from the cycle, which means that at least one vertex from the cycle will be replaced by a number that is not the next vertex in the cycle, which is incorrect because each vertex from the cycle should be replaced by the next vertex after it. If the size of the cycle is greater than $$$k$$$, then we will have a vertex from the cycle that will be replaced by a vertex that is not the next vertex in the cycle (otherwise we would have used all the vertices of the cycle, and there are more than $$$k$$$ of them). Therefore, in any case, there is no valid last operation with vertices from the cycle, so the answer is NO.
If the size of the cycle in a component is equal to $$$k$$$, then we can apply the following algorithm:
While there is at least one vertex $$$v$$$ in the component that is a leaf, we will perform the operation with $$$l = [v, b_v, b_{b_v}, \cdots]$$$ (all elements are distinct because we will enter the cycle and it has a size of $$$k$$$). After this operation, we will have $$$a_v = b_v$$$, and we can remove vertex $$$v$$$ (it had only $$$1$$$ outgoing edge).
When only the cycle remains, we can apply the operation for the vertices in the cycle, preserving the order, and then for all vertices in the component, we will have $$$a_v = b_v$$$. By doing this for all components, we will get $$$a = b$$$, which is what we wanted, so the answer is YES.
Time Complexity: $$$O(n)$$$ per test case.
#include <bits/stdc++.h>
using namespace std;
int main()
{
ios_base::sync_with_stdio(false);
cin.tie(0);
int t;
cin >> t;
while(t--)
{
int n,k;
cin >> n >> k;
int b[n];
int vis[n];
for(int j = 0;j < n;++j)
{
cin >> b[j];
vis[j] = 0;
}
if(k == 1)
{
int no = 0;
for(int j = 0;j < n;++j)
{
if(b[j] != j+1)
{
no = 1;
}
}
cout << (no ? "NO\n" : "YES\n");
continue;
}
int num[n];
int no = 0;
int tgr = 1;
for(int j = 0;j < n;++j)
{
if(!vis[j])
{
int ind = j;
int cnum = 0;
while(!vis[ind])
{
vis[ind] = tgr;
num[ind] = cnum++;
ind = b[ind]-1;
}
if(vis[ind] != tgr)
{
tgr++;
continue;
}
if(cnum-num[ind] != k)
{
no = 1;
break;
}
tgr++;
}
}
cout << (no ? "NO\n" : "YES\n");
}
}
1867E1-Salyg1n and Array (simple version)
Author: salyg1n
Let's make queries to subarrays starting at positions $$$1$$$, $$$k + 1$$$, $$$2k + 1$$$, $$$\ldots$$$ $$$m \cdot k + 1$$$, as long as these queries are valid, meaning their right boundary does not exceed $$$n$$$. Let's save the $$$\operatorname{XOR}$$$ of all the answers to these queries. We will call these queries primary.
Now, we will shift the last subarray of the query one unit to the right and make a new query, as long as the right boundary does not exceed $$$n$$$. We will call these queries secondary. It is claimed that the $$$\operatorname{XOR}$$$ of the entire array will be equal to the $$$\operatorname{XOR}$$$ of all the queries. Let's prove this.
Let $$$i$$$ be the position at which the first secondary query starts. Notice that after this query, the subarray [$i$; $$$i + k - 2$$$] will turn into the subarray [$$$i + 1$$$; $$$i + k - 1$$$] and reverse. After the next query, the same thing will happen, the subarray will shift one unit to the right and reverse. Therefore, the prefixes of length $$$k-1$$$ of each secondary query will be the same, up to the reversal, which does not affect the $$$\operatorname{XOR}$$$. Since the number of secondary queries is equal to $$$n \operatorname{mod} k$$$, which is an even number, the $$$\operatorname{XOR}$$$ of these prefixes will not affect the $$$\operatorname{XOR}$$$ of all the secondary queries, which will therefore be equal to the $$$\operatorname{XOR}$$$ of the elements [$a_{i + k — 1}$; $a_n$], that is, all the elements that we did not consider in the primary queries.
The number of primary queries is equal to $$$\lfloor \frac{n}{k} \rfloor \leq k \leq 50$$$, since $$$n \leq k^2 \leq 2500$$$.
The number of secondary queries is equal to $$$n \operatorname{mod} k < k <= 50$$$, since $$$k^2 \leq 2500$$$.
The total number of queries does not exceed $$$100$$$.
#include <iostream>
using namespace std;
int ask(int i) {
cout << "? " << i << endl;
int x;
cin >> x;
return x;
}
void solve() {
int n, k;
cin >> n >> k;
int res = 0;
int i;
for (i = 1; i + k - 1 <= n; i += k)
res ^= ask(i);
for (; i <= n; ++i)
res ^= ask(i - k + 1);
cout << "! " << res << endl;
}
int main() {
int t;
cin >> t;
while (t--)
solve();
return 0;
}
1867E2-Salyg1n and Array (hard version)
Author: salyg1n
Let's make queries to subarrays starting at positions $$$1$$$, $$$k + 1$$$, $$$2k + 1$$$, $$$\ldots$$$ $$$m \cdot k + 1$$$, such that the size of the uncovered part is greater than $$$2 \cdot k$$$ and not greater than $$$3 \cdot k$$$. In other words, $$$2 \cdot k < n - (m + 1) \cdot k \le 3 \cdot k$$$. Let's keep the $$$\operatorname{XOR}$$$ of all the answers to these queries. We will call these queries primary.
Let the size of the remaining (uncovered) part be $$$x$$$ ($$$2 \cdot k < x \le 3 \cdot k$$$). Let's learn how to solve the problem for an array of size $$$x$$$ in three queries.
If $$$x = 3 \cdot k$$$, simply make queries to positions $$$1$$$, $$$k + 1$$$, $$$2 \cdot k + 1$$$.
Otherwise, let $$$y = x - k$$$. Note that $$$y$$$ is even, since $$$x$$$ and $$$k$$$ are even.
Make queries at positions $$$1$$$, $$$1 + \frac{y}{2}$$$, $$$1 + y$$$.
Note that after this query, the subarray [$1$; $$$k - \frac{y}{2}$$$] will turn into the subarray [$$$y/2 + 1$$$; $$$k$$$] and reverse. After the next query, the same thing will happen, the subarray will shift one unit to the right and reverse. Therefore, the prefixes of length $$$k - \frac{y}{2}$$$ for each query are the same, up to the reversal, which does not affect the $$$\operatorname{XOR}$$$. Since the number of queries in the second group is $$$3$$$, which is an odd number, the $$$\operatorname{XOR}$$$ of these prefixes will be taken into account exactly once in the $$$\operatorname{XOR}$$$ of all the queries, which will therefore be equal to the $$$\operatorname{XOR}$$$ of the elements.
The number of primary queries does not exceed $$$\lfloor \frac{n}{k} \rfloor \leq k \leq 50$$$, since $$$n \leq k^2 \leq 2500$$$.
The total number of queries does not exceed $$$53$$$.
#include <iostream>
using namespace std;
int ask(int i) {
cout << "? " << i << endl;
int x;
cin >> x;
return x;
}
void solve() {
int n, k;
cin >> n >> k;
int res = 0;
int i;
for (i = 1; n - i + 1 >= 2 * k; i += k)
res ^= ask(i);
if (n - i + 1 == k) {
res ^= ask(i);
cout << "! " << res << endl;
return;
}
int y = (n - i + 1 - k) / 2;
res ^= ask(i);
res ^= ask(i + y);
res ^= ask(i + 2 * y);
cout << "! " << res << endl;
}
int main() {
int t;
cin >> t;
while (t--)
solve();
return 0;
}
Author: green_gold_dog
Here we say that the answer for tree $$$G'$$$ is the number of subtrees in $$$P(G')$$$ that have an isomorphic subtree in $$$P(G)$$$.
Let's find a tree $$$T$$$ of minimum size that has no isomorphic tree in $$$P(G)$$$. Let the size of tree $$$T$$$ be $$$x$$$. Then take a chain of size $$$n - x$$$, and let the root of $$$T$$$ be the kid of the last vertex on the chain. We say that this is the tree $$$G'$$$ we were looking for (with the root of $$$G'$$$ being the first vertex of the chain). The number of matching subtrees will be at most $$$x - 1$$$, since all subtrees of the vertices on the chain and the subtree $$$T$$$ itself will not have isomorphic trees in $$$P(G)$$$, because $$$T$$$ lies entirely in them, and $$$T$$$ has no isomorphic tree in $$$P(G)$$$. Therefore, the answer is not greater than $$$n - (n - x) - 1 = x - 1$$$.
Let's prove why the answer cannot be less than $$$x - 1$$$: suppose there exists a tree $$$G*$$$ for which the answer is less than $$$x - 1$$$. Let's find a subtree of minimum size whose size is at least $$$x$$$ (it always exists, since we can take the entire tree for example). In this subtree, there are at least $$$x - 1$$$ other subtrees, whose sizes are less than $$$x$$$ (because in the previous step we chose a subtree of minimum size not less than $$$x$$$). And since all trees of size less than $$$x$$$ have isomorphic trees in $$$P(G)$$$ (by definition $$$T$$$ is the tree of minimum size that has no isomorphic tree in $$$P(G)$$$ and its size is $$$x$$$), the number of matching subtrees in tree $$$G*$$$ is at least $$$x - 1$$$, which is a contradiction.
Therefore in our case the answer is $$$x - 1$$$.
Now let's solve the second part of the problem — finding $$$T$$$. To do this, let's first find all trees of size 1, then of size 2, then 3, 4 and so on until we find a tree that has no isomorphic subtree in $$$P(G)$$$. One can see that if we generate all trees of size up to 15 we will definitely find $$$T$$$ there. Within each size, let's number the trees in the order in which we've generated them. To find all trees of size $$$x$$$ if we are given all trees of size $$$x - 1$$$ and smaller, let's say that the sizes of the children of the root of the tree we generate must not decrease, and if the sizes are the same, their positions in the order must not decrease. Then, we can iterate over the first child, then among the smaller and suitable ones, the second child, then the third, and so on until the total size of the tree becomes exactly $$$x$$$. This way, we will enumerate all trees of size $$$x$$$ in complexity of their total number (since we will not consider any tree twice and will not consider any extra trees). Let's do this until we find a tree that is not in $$$P(G)$$$.
Hashes can be used to compare trees for isomorphism. For more details, read the blog post
Time Complexity: $$$O(n \log n)$$$.
#include <bits/stdc++.h>
using namespace std;
const int MAXSZ = 15;
void rec(int ns, int last, vector<int>& now, vector<vector<int>>& aint, vector<int>& col, vector<int>& sz, int& ss, int sns) {
if (ss < 0) {
return;
}
if (ns == 0) {
col.back()++;
aint.push_back(now);
ss -= sns;
return;
}
for (int i = min(last, col[ns] - 1); i >= 0; i--) {
now.push_back(i);
rec(ns - sz[i], i, now, aint, col, sz, ss, sns);
now.pop_back();
}
}
void dfs(int v, int p, vector<vector<int>>& arr, vector<int>& num, map<vector<int>, int>& m, vector<int>& sz) {
vector<int> now;
sz[v] = 1;
for (auto i : arr[v]) {
if (i != p) {
dfs(i, v, arr, num, m, sz);
sz[v] += sz[i];
if (sz[v] <= MAXSZ) {
now.push_back(num[i]);
}
}
}
if (sz[v] > MAXSZ) {
num[v] = -1;
return;
}
stable_sort(now.begin(), now.end());
reverse(now.begin(), now.end());
num[v] = m[now] - 1;
}
void dfs2(int x, int p, vector<vector<int>>& aint, vector<int>& ans) {
if (p >= 0) {
ans.push_back(p);
}
int now = ans.size();
for (auto i : aint[x]) {
dfs2(i, now, aint, ans);
}
}
void solve() {
int n;
cin >> n;
vector<vector<int>> aint(1);
vector<vector<int>> arr(n);
for (int i = 1; i < n; i++) {
int a, b;
cin >> a >> b;
a--;
b--;
arr[a].push_back(b);
arr[b].push_back(a);
}
map<vector<int>, int> m;
vector<int> col(1, 0), sz(1, 1);
col.push_back(1);
for (int i = 2; i <= MAXSZ; i++) {
vector<int> now;
col.push_back(col.back());
int ss = n;
rec(i - 1, aint.size() - 1, now, aint, col, sz, ss, i);
while (sz.size() < col.back()) {
sz.push_back(i);
}
if (ss < 0) {
break;
}
}
for (int i = 0; i < col.back(); i++) {
m[aint[i]] = i + 1;
}
vector<int> num(n), szi(n, 1);
dfs(0, 0, arr, num, m, szi);
set<int> s;
for (int i = 0; i < col.back(); i++) {
s.insert(i);
}
for (auto i : num) {
s.erase(i);
}
int x = *s.begin();
vector<int> ans;
if (sz[x] > n) {
for (int i = 0; i < n; i++) {
for (auto j : arr[i]) {
if (i < j) {
cout << i + 1 << ' ' << j + 1 << '\n';
}
}
}
return;
}
for (int i = 0; i < n - sz[x] - 1; i++) {
ans.push_back(i);
}
dfs2(x, n - sz[x] - 1, aint, ans);
for (int i = 0; i < ans.size(); i++) {
cout << ans[i] + 1 << ' ' << i + 2 << '\n';
}
}
int main() {
ios_base::sync_with_stdio(false);
cin.tie(0);
cout.tie(0);
int t = 1;
//cin >> t;
for (int i = 0; i < t; i++) {
solve();
}
}










If you were wondering why am I an author but didn't make any problems: a day before the contest we decided to replace my task F (because I hate it) and to give "Most Different Tree" instead, hopefully it fits better (I guess we'll never know) :]
Video Editorial for A-E2 ...I hope it will helpful to Newbies and Pupils..! YOUTUBE EDITORIAL LINK
In 1867E2 - Salyg1n and Array (hard version) it is impossible to achieve $$$2k < x$$$ if $$$n \leq 2k$$$. However, in fact we do not need this condition. The second part of the solution still works in the case $$$k < x \leq 2k$$$.
E2 can be actually done in 51 operations instead of 57.
When k divides n then it only takes n/k queries, i.e 50 at max.
Otherwise, we can separate the first n*[n/k] elements and the remaining n%k elements. Since, n%k is even then we can divide those remaining elements in 2 parts of (n%k)/2 size. First, we ask a query where the i+k-1=n-(n%k)/2. Then after the subarray gets reversed, we again ask another query where i+k-1=n. Taking XOR of their outputs, the common elements gets nullified and we get our requried value.
This takes [n/k]+2=49+2=51 queries.
Submission E2
Nice solution!
Here's a sort of visual proof of why this works: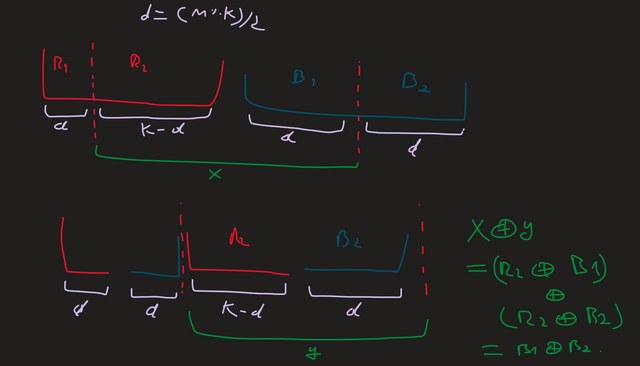
Yeah, we know, our solution does 51 queries too. Number 57 is just cool. Also the limit of 51 quiries could be a hint
Nice! Easy to understand!
lol
Disclaimer: I'm a stupid newbie code Note: Yet plz continue reading Many accepted solutions, including this official editorial solution, are giving answers other than the correct answer (1) for the following test case:
t=1 n=9 k=4 array = [1, 2, 3, 4, 5, 6, 7, 8, 9]The problem statement mentions both n and k will be even
Yeah, you just answered your own question.
The necessity to learn C++ to literally write the same code for Problem C pisses me off. TLEs in Java :(
Thank you for editorial <3
runtime error @testcase3 for D, grateful if someone can find the error ! fk this shit mann!
Python has a default maximum recursion depth of 1000. Since n is of the order 2e5, it is not possible to do it in a recursive fashion. Try writing your dfs using stacks or just use while loops.
Note that you may also try increasing the recursion depth limit ( sys.setrecursionlimit(N) ) but that would just lead to MLE.
what's MLE
Memory limit exceeded
It was possible to make problem E1 and E2 more interesting by pushing extra condition (n+k)%2==0.
In the problem 1867E2 — Salyg1n and Array (hard version) for a case where n = 3, k = 2 and a = [4, 2, 5] the answer should be 3. But the given solution in the editorial is providing the answer 6. The interaction is given below,
Can someone explain the case?
Read problem statement clearly , here n and k always even. And the information you got ,is not enough.
Thank you. I should have been more careful.
Can someone please explain why was this submission skipped https://codeforces.com/contest/1867/submission/222952890 ? It have gotten AC on pretests and i also sent almost identical one (added pragmas) later and it got AC.
Because later you submitted another submission and it also passed pretests. Only your last AC submission is tested on sistests
OK, thanks. It wasn’t the case for previous contests as far as i remember though…
वीडियो स्पष्टीकरण A,B,C,D
bhaiya i watched the video but not able to get the B what should i do
223167780
Can anyone give me an edge case which should give wrong answer for this code?
I was too lazy to code some general tree enumeration for F, so I got a slightly different solution.
Expand a little on the jury's observations. The answer always (except for $$$n=2$$$) looks like that: some tree that is not in $$$P(G)$$$, all its children are in $$$P(G)$$$ and there's a long bamboo attached to its root. The value of the answer is the sum of the sizes of the children.
Now, recall the hashing part of the isomorphism check procedure. We take the isomorphism classes of all children of a vertex, sort them and get the class of the whole tree based on that list. Imagine building the answer with that procedure. The resulting list should not appear among the existing classes. However, during the procedure, all prefixes of the list have to appear among them. Otherwise, we could've taken that prefix as the answer.
Thus, the answer looks like that: an existing subtree with another existing subtree attached to it as the last child. Additionally, the class of the last child should be not less than the class of the last child of the initial subtree.
So the solution could look like that. Iterate over the existing classes as the initial tree, then iterate over them again as the last child. If the last child is smaller than the last element of the initial list, skip it. If the list with the new element appended appears among the existing classes, skip it. Find the smallest tree among everything that's left.
Unfortunately, it's too slow as is. Let's optimize.
The second condition is easy to circumvent. Find all existing lists that are the current one with one element appended. You can think of it as building a trie of these lists, then traversing it. Now, you can remove them from some structure of options, then find the best option, then add them back. That would be $$$O(n)$$$ removals and additions in total.
The first condition is harder. I chose to abuse the fact the answer is really small. For each size, store the indices of the classes of all existing trees of that size in the increasing order. Now, we can iterate over the size of the option tree, then lower_bound for the index that is at least as large as the last element of the current list. If the iterator isn't at the end, update the answer and break. If you use a set for that, you can easily support the removals and additions as well.
I believe, that is $$$O(n \cdot \mathit{ans} \cdot \log n)$$$. The submission is 222999827 if anyone is curious.
Can someone please explain why in the A problem I cannot use a multimap?
I think you mixed up the position of the first element of the sorted array in the original array with the position of the first element of the original array in the sorted array.
Do anyone know 42th subtest of test 2 of problem D. I can not pass this anyway
In the editorial of F it is said that "One can see that if we generate all trees of size up to 15 we will definitely find T there."
How do you prove that we only need trees with a size no more than 15?
Because the number of rooted trees of size 15 is more than $$$87000$$$. $$$87000 \cdot 15 > 10^6$$$, so the initial tree can't have all these trees as subtrees. Here's the sequence
ace5, can you please tell me for the problem 1867D - Cyclic Operations what is the motivation for converting this problem into graph . Its just something outside of my thought process that this problem can also be thought like this. So how we actually know of converting it. Is it by just applying other concepts and then checking if they are not working then try another some new concept.
Because i have been thinking like that for the answer to be YES , all the elements in the array must have been permutation of the positions and then are overlapped in a unique fashion and if this condition does not hold somewhere in between then the answer will be NO. But i do not know how we will implement it and just went blank after that.
Can you please explain it will be so kind of you as i have spent a significant amount of time but still have no idea.
.
A much more sane way to implement F is to recognize that you can enumerate all RBS of length 28 to cover the euler tour of every tree of size 15 (with repetitions); there are 2.6e6 of them which barely fits in the TL. However, you can also use this method for sizes up to 14 and just use random to solve size 15 (less than 80% of size 15 trees can be subtrees), which should reduce the runtime by a factor of 3.6 and comfortably pass.
https://codeforces.com/contest/1867/submission/223380152
I want to ask In problem E: how come this sample is accepted n=3 k=2 and the array is 1 2 4 the judges code is answering 6 when in fact it should be 7 but there is no definite way to know the answer.
Notice that problem statement states n and k are even numbers. It can be shown that this ensures uniqueness of the answer.
In E1/E2, if anyone is wondering if solution for any cases where n & k are not both even is possible or not. I tried some examples and found out that I can construct a solution if k is odd (doesn't matter whether n is odd or even). But when k is even we can prove that solution is not possible if n is odd.
Initially, we can only get xor of even subarray sizes. Now, let's say there are 2 sets of even size (say x & y). And t elements are common in these 2 sets, after taking xor of these 2 sets we again get new set of even size i.e. x + y — 2t. So, constructing a set of odd size i.e. n is not possible when k is even.
Note: Can someone please confirm my claim or prove me wrong?
For problem F, I can't understand why I got wa for this code. Who can help me find out the problem please qwq. https://mirror.codeforces.com/contest/1867/submission/223794337
Hi everyone its really hard for me to understand problem D. I have watched many videos and editorial but not able to understand problem D . Can anyone tell me what should I do?
So, the idea is first to understand how the operation works. You can try some examples with 1 2 3 4 and play with it(reverse order of them). You will realise: you cant get a number on its index(1 cant stay on first index, 2 on second...), and you must go in cycle to come back to 1(if you set first index to 3, index 3 must be 2 or 4 lets say 4, index 4 can be only 2 and index 2 1). After that try to do example: k = 4, array = 2 3 4 1 1, you will understand that you can do 1 operation to get 1 on fifth index and after that do operation on first 4 to solve them. So the conclusion is: if you have a good cycle of 4(cycle where all numbers remain in their indexes:3 5 4 5 1 5 5 5 example where indexes 1 3 4 5 are a good cycle, you can first solve for all other indexes that have one of those 4 numbers and then solve the cycle), but if you have a cycle of 3 when k is equal 4 you cant solve the problem(you can make only 4 cycle rotations). So the problem becomes finding good cycle indexes and all other indexes that have good cycle indexes as value and hoping that after finding all of those whole array is done. So we need to find cycles between numbers and their connections to rest of the array which is nothing more than a graph.
why hacks in third problem are forbidden?
Can some one explain in problem D, what is the insight that leads to constructing a directed graph with edges going from i to b[i] ? Specifically, why use edges from i to b[i] ?
for(int j = 0;j <= max_2;++j) { for(int k = 0;k <= max_1;++k) { t[ans + j*2 + k] = '1'; } } in B can you explain this part