Introduction to Disjoint Set Data Strucutres
Hello Codeforces!
I recently read about Disjoint Sets from the book Introduction to Algorithms and wanted to share the learnings in a simplified manner.
So below article(and corresponding videos) is an attempt to create a good starting point for people who:
- want to learn about DSU
- practice some good DSU problems
Contents
- Introduction through an illustrative problem (video version: https://youtu.be/JDycPHW4kIs?si=WEp5Ft2jBWp9KnO2)
- Sample SPOJ Problem and Implementation (video version: https://youtu.be/O4w-aX5mSks?si=vr0XSbyUswcXx-Yv)
- Upcoming Practice Problems
- Some Applications and References
We will learn about disjoint set data structures and their operations union and find through a sample problem.
Illustrative Problem
Q: Given a undirected $$$Graph(V, E)$$$, answer Q queries of the form $$$(u, v)$$$ where answer to the query is True if there is a path from u to v, false otherwise. 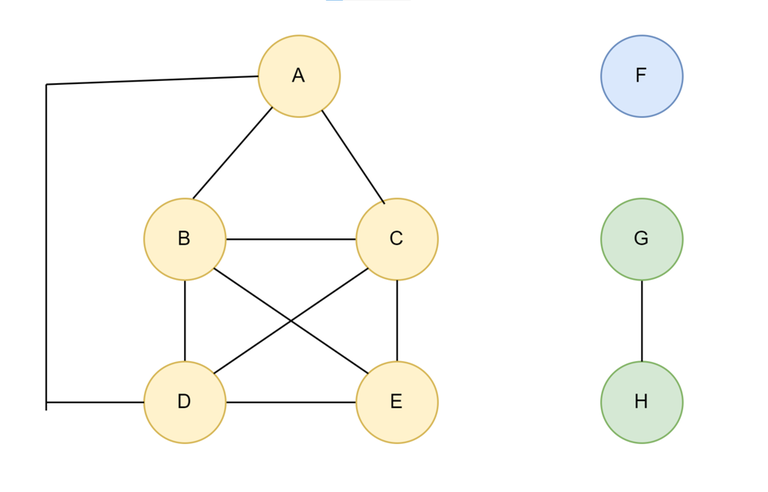
So for above graph:
- $$$query(D,A)$$$ = true
- $$$query(D,C)$$$ = true
- $$$query(D,F)$$$ = false
Some solutions to above problem
Solution1:
- For each query $$$(u, v)$$$, perform a BFS/DFS.
- Time Complexity will be $$$O(Q*(V + E))$$$
- In worst case graph can have order of $$$V^2$$$ Edges.
- So worst case complexity can be $$$O(Q*V^2)$$$
Solution2:
- perform 1 BFS/DFS per node of the Graph
- When BFS is done using node X, store all the nodes that can be visited from X.
- Per Query time is $$$O(1)$$$ so overall $$$O(Q)$$$
- Preprocessing time is $$$O(V * (V + E)) = O(V^3)$$$
- Hence overall $$$O(Q + V^3)$$$
What is a Disjoint Set Data Structure?
- It is a collection of disjoint dynamic sets. $$$D = {S1, S2, S3, …………, Sk}$$$
- Each set has a Representative R and consists of some elements.
- Assume total elements is N: $$$Size(S1) + Size(S2) + … + Size(Sk) = N$$$
A disjoint set structure supports:
- $$$MAKE-SET(X):$$$ Creates a new Set with only element X and representative X.
- $$$FIND(X):$$$ Returns the representative of the set to which X belongs.
- $$$UNION(X, Y):$$$ Unites the sets containing the elements X and Y into a single new Set. The representative of this set is usually either the representative of Sx or representative of Sy
Diagramatic Example of a disjoint set with total 8 elements and 3 sets:
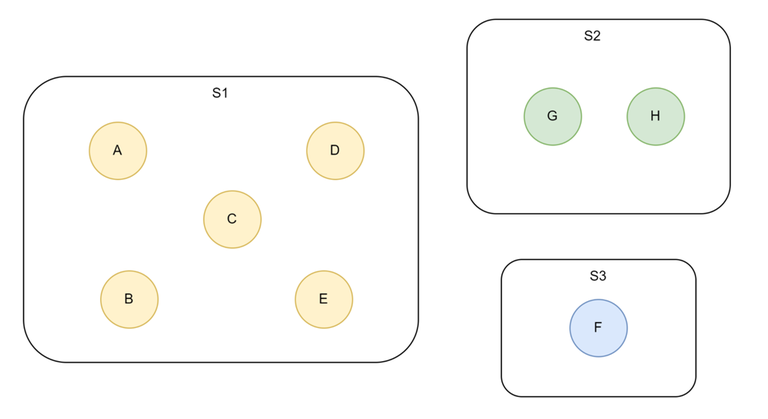
From above:
- $$$Find(H) = G$$$
- $$$Find(F) = F$$$
- $$$Find(B) =Find(E) = A$$$
[Assume that A, G and F are representative elements their sets]
Using Disjoint Set DS for solving the problem
- Run $$$MAKE-SET(u)$$$ for each of the V nodes in the graph.
- Run $$$UNION(u,v)$$$ for each edge $$$(u,v)$$$ in the graph.
- For each Query (u,v): a) If $$$FIND(u) == FIND(v)$$$ then answer = true b) Else answer = false
Running 1. and 2. on sample graph constructs the Disjoint set data structure shown in diagram.
Time complexity for DSU solution
Overall Complexity is sum of:
- $$$O(V * MAKE-SET)$$$
- $$$O(E * UNION) = O(V^2 * UNION)$$$
- $$$O(Q * FIND)$$$
Disjoint Set — Linked List Implementation
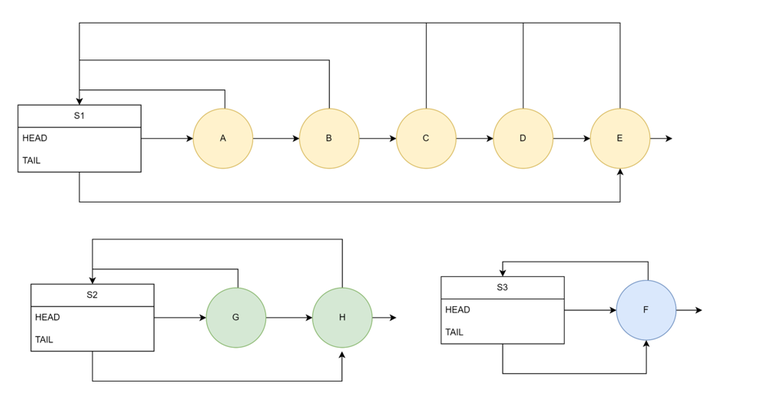
- Each set is represented as a link list.
- The set has HEAD pointer to representative element and also a TAIL pointer.
- Each element of the set has a back-pointer to the set.
Complexity Analysis for link list implementation
- Make Set is O(1) -> only need to create a new set with 1 element
- Find Set is O(1) -> thanks to back pointers
- Union is length of the longer set -> no-thanks to back pointers(all of 2nd set element back-pointers need to be updated to 1st set)
Note: For a total of N elements in the collection there will be at most N-1 union operations as post that all elements will be in the same set.
Worst Case cost of Union is when:
- All sets have size 1.
- 1st union we unite two sets of size 1 and get a set of size 2 -> cost is 1 back pointer change.
- 2nd time we unite a set of size 1 with a set of size 2 -> cost is 2 back pointer change.
- ith time we unite a set of size 1 with a set of size i -> cost is i back pointer change.
- Overall cost over n-1 union operations is $$$1 + 2 + 3 + .. + n-1 = O(N^2)$$$
Hence union is still $$$O(N)$$$ in the worst case.
Weighted Union Heuristic for link list Implementation
While performing $$$union(x,y)$$$:
- Always take smaller set and attach it the larger set.
- Need to maintain size of set for each set(which should be easy)
Complexity analysis: Union is now $$$O(logN)$$$, but why?
- The cost of a union operation is the cost of changing back pointers of the elements in the smaller set.
- Say we change the back pointer of an Element X belonging to $$$S_x$$$, the resulting set will have at least $$$2 * S_x$$$ elements.(since X belong to smaller set and hence it's backpointer was updated)
- If back pointer of X is changed K times there need to be $$$>= (2^K) * S_x$$$ elements
- K can be at most log(N) as we only have N elements.
- hence for a given element we can change the back-pointer at most logN times and overall cost $$$<= NlogN$$$
Revisiting the sample problem
Worst Case complexity of Graph problem has now Improved :)
- $$$O(V * MAKE-SET) = O(V)$$$
- $$$O(E * UNION) = O(V^2 * UNION) = O(V^2 * logV) = O(V^2 * logV)$$$
- $$$O(Q * FIND) = O(Q)$$$
So $$$O(V^2 * logV)$$$ instead of $$$O(V^3)$$$
Disjoint Set — Forest Implementation
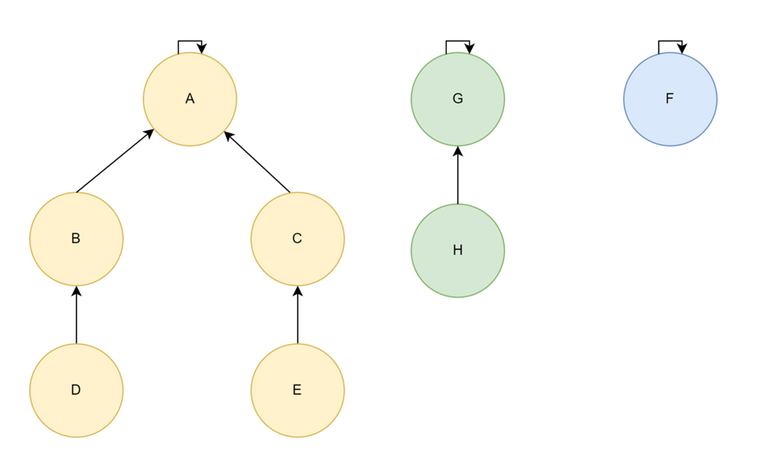
- Each set is represented as a tree.
- Each element is a node of the tree and maintains a pointer to it's parent in the tree.
- The representative element is the parent of itself.
$$$Find(X) = X \;if\,parent[X] = X \;else\,Find(X) = Find(parent[X])$$$
Forest Implementation — Time Complexities
We may still end up getting a chain :(
Worst case complexities:
- UNION is $$$O(1) * O(FIND)$$$ in worst case(only need to change parent pointer of one representative to another, problem is finding the representative using FIND)
- MAKE SET is $$$O(1)$$$ in worst case(only need to create a set with 1 element which is it's own parent)
- FIND however is $$$O(N)$$$ in the worst case(we may end up getting a link list)
Time Complexities with Heuristics
Heuristic: Union by Rank
While performing union always take the Set(tree) with less height and attach it to the set with greater height.
- Overall height after N-1 union will be order of LogN
- Hence ensuring Find is no worse than LogN
Heuristic: Path Compression When performing find operation, change the parent pointer of each node to the actual representative of the node. 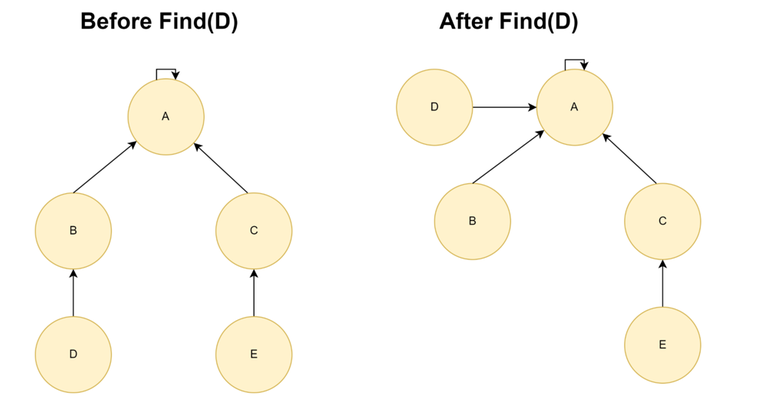
The time complexity when applying both heuristics together is:
- Make Set is $$$O(1)$$$
- Find Set is $$$O(\alpha(n))$$$
- Union is amortised $$$O(\alpha(n))$$$
What is $$$\alpha(n)$$$?
- Where alpha is the inverse of Ackerman function $$$A_k(1)$$$
- $$$\alpha(n) <= 4$$$ for all $$$N <= 16^{512}$$$
- $$$16^{512}\; »\; 10^{80}$$$
- $$$10^80$$$ is the number of atoms in observable universe
Hence for all practical purposes $$$\alpha(n) = 4 = constant$$$.
Proof is harder and omitted from scope of this article, refer Introduction To Algorithms by Thomas H. Cormen
Revisiting the sample problem
- Make Set is $$$O(1)$$$
- Find Set is $$$O(1)$$$
- Union is $$$amortised O(\alpha(n))$$$
Worst Case complexity of Graph problem has now Improved :)
- $$$O(V * MAKE-SET) = O(V)$$$
- $$$O(E * UNION) = O(V^2 * UNION) = O(V^2 * logV) = O(V^2 * \alpha(V))$$$
- $$$O(Q * FIND) = O(Q)$$$
Hence time complexity is now $$$O(V^2 + Q)$$$ for all practical purposes.
SPOJ Problem — FRNDCIRC + Generic Implementation
- Problem Link: https://www.spoj.com/problems/FRNDCIRC/
- Solution link: https://youtu.be/O4w-aX5mSks?si=UQJwpjayddjVK5uw
- Code implementation: https://ideone.com/Bdh2It
Upcoming Practice Problems
Currently I have planned the problem https://codeforces.com/problemset/problem/150/B and will be soon adding both a written and video editorial for the same.
Few other practice problems include: https://codeforces.com/blog/entry/55219?#comment-390897 (DSU tag). I will be using some of these to create more editorials.
If you have more suggestions please add in comments.
Applications and References
Some direct applications:
- Finding cycles in a graph
- Kruskals minimum spanning tree algorithm
Some references:
- https://www.youtube.com/@AlgosWithKartik
- Introduction to Algorithms Book
- CP algorithms: https://cp-algorithms.com/data_structures/disjoint_set_union.html










Hard to read, learn $$$L^AT_EX$$$ first please.
done, I guess looks better now.
Pretty cool Kartik, thank you!
Welcome mate :)
The example problem doesn't really make any sense in this context. You can just do a single dfs for each unvisited node to find all components in $$$O(V + E)$$$ which in the worst case is $$$O(V + V^2) = O(V^2)$$$. Now you can solve all queries in true $$$O(Q + V^2)$$$ without dsu.
Thankyou for the solution!
Note: I came up with the problem(in a brief time) that may utilise DSU and thought it to be useful to illustrate the working and use of a Disjoint Set DS. No claims on if the solution is the most optimal.
I personally feel it's good to use a simple problem and show how the topic being learnt can be applied to solve it.
Also In my knowledge it's fairly common for tutorials, books and educational articles to use simple problems for highlighting the use of some techniques where the technique may not necessarily be the most optimal to solve the problem(example: range min queries with point updates is a common example for segment tree tutorials which is better solved using a sparse tree)
Again, the style of authoring and explaining is subjective so you might disagree :)
I mostly agree with what you stated and I was probably too harsh in my original comment, sorry about that.
I understand that example problems can have more optimal solutions than the one you're describing. I just think that the solution I mentioned is actually easier to understand than DSU and that's why I didn't like the fact that you portrayed DSU here as a special technique to solve this problem fast.
I think a better example problem would've been to start with an empty graph and add a new type of query: connect nodes $$$u$$$ and $$$v$$$. This would've forced the use of DSU but also showcased better that DSU can handle online edge additions with no extra time wasted. But maybe people also realized that from your current explanation, and my criticism is not very useful.
Makes sense! Thanks for the detailed comment. Will try thinking of better illustrative problems for future blogs(or maybe pick something from SPOJ).
For current blog will be adding more problems so should make up for anything that got missed.