I was reading about hashing from here and I am unable to understand the part about calculation of hash of a substring. I am calculating the hash of the entire input string in this way : h (S) = S [0] + S [1] * P + S [2] * P ^ 2 + S [3] * P ^ 3 + ... + S [N] * P ^ N
Suppose P = 31 and a = 1, b = 2, c = 3 and so on. Then for the input string abcdab, h[0] = 1, h[1] = 32, h[2] = 2915, h[3] = 122079, h[4] = 1045600, h[5] = 58303902. Now from these values, how can I calculate h[0..1] or h[3..5]?











Let's store suffix hashes instead.
We can now calculate hashes like that:
h[i] = h[i + 1] * p + s[i]So, we want to find h[l..r]. Let
len = r - l + 1Let's write h[l] and h[r + 1]:
That's exactly what we need.
Thanks for replying. Can you also tell me how can I use this for longer strings, say
len = 10000.P^lenwill not fit in 64-bit int and I read this which suggests that we shouldn't do calculations mod 2^64. So, whatmodshould I use and how can I calculate hash of a substring when doing calculations mod some number?You should always use a prime modulo, for example,
10^9 + 7or10^9 + 9. You can do all the operations by that modulo. Just calculate powers ofpby that modulo, all calculations will be fine.BTW, when you substract 2 numbers by modulo, you can get a negative number in result. If you use just
a % b, in many programming languages it would be negative. For example you can usecout << -3 % 2;, it'll output -1, but you would expect 1. So, the best way to prevent negative numbers is using(a % b + b) % b. For example a = -3, b = 2:(-3 % 2 + 2) % 2 = (-1 + 2) % 2 = 1 % 2 = 1can you explain where i have to use (a % b + b) % b in this code http://codeforces.com/contest/182/submission/6734689 i think my error is because of this.
So, we want to know, what is remainder if we divide a by b. As you know, mathematical remainder always belongs to the range of [0, b)
So, if we write
a % b, we expect to get the remainder. If a >= 0 we'll indeed get the remainder. But if a < 0 we'll not get the remainder (in most languages: C++, Java, but not Python). But actually, if we addbto this, we'll get the remainder (it will be in range (-b, 0]).For example:
So, if we write
a % b + b, we'll always get a positive integer. In case of negative a, it will be the remainder. In case of a non-negative a, it will ber + b. To get a true remainer, we'll write(a % b + b) % b. This will work for all positive values of a.hey thanks a lot for replying. i understood your comment but can you please tell the reason the code posted in this comment http://codeforces.com/blog/entry/12145#comment-171463 is giving negative hashes for some substrings. thanks.
someone please answer this. i have been working on this problem since a long time..is the hashing technique correct?
You can use unsigned type , and forget about negative
here my example
http://community.topcoder.com/stat?c=problem_solution&rm=320487&rd=15840&pm=12967&cr=22853961
You can also use a pair of hashes, both of which are computed modulo a different prime. That way you get much better collision resistance and you don't need to multiply 64-bit numbers.
can you please tell wy i get negative value for some hashes? http://ideone.com/OgspSn dfferent base and MODs give different results.some give negative values some dont. why is it so and how can i get rid of this? this one's same as previous code but with different MOD http://ideone.com/HWtRxk but even this gives WA 3.
What? No, I'm not going to debug your code. But chances are good that you have an overflow in there.
#comment-171465
Try writing separate function for calculating
x % MODsuppose we have this:
can we get hash(l, r) in O(1)?
Of course! o.0
Just store powers of
p! Now the result will beh[l] - h[r + 1] * ppow[r - l + 1]thanks.
Here's the implementation in CPP.
same
Anti-hash test is coming for you, so don't forget to make all the calculations by some modulo!
Here's my implementation:
I think this one's correct too. Anyways, thanks a lot for our help. Can you also suggest a few problems that can be solved by hashing?
the second one (with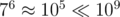 . ur second code wouldn't work without
. ur second code wouldn't work without 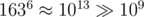 .
.
#define BASE 163) is the correct way to do it.having said that, ur first code (despite not having
MOD) was "right" becauseMODaswhat if h[l] lesser than h[r+1] * p^len?? i will obviously get negative value.
I've already wrote about it, do you support reading the text?
Great method !