If you have any questions or suggestions, or if you have a solution different to ours that you want to share with us, feel free to comment below :)
Author solutions are added.
Div. 2 A — Kitahara Haruki's Gift
Denote G as the sum of the weight of the apples. If G / 100 is not an even number, then the answer is obviously "NO". Otherwise, we need to check if there is a way of choosing apples, so that the sum of the weight of the chosen apples is exactly 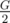 .
.
A simple O(n) approach would be to enumerate how many 200-gram apples do we choose, and check if we can fill the rest with 100-gram apples. We can also solve this problem using a classic knapsack DP.
Solution: 6712942
Div. 2 B — Kuriyama Mirai's Stones
Sort sequence v to obtain sequence u. Sorting can be done in  using quicksort. Now we are interested in the sum of a interval of a given sequence. This can be done by calculating the prefix sum of the sequence beforehand. That is, let
using quicksort. Now we are interested in the sum of a interval of a given sequence. This can be done by calculating the prefix sum of the sequence beforehand. That is, let 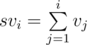 . The sum of numbers in the interval [l, r] would then be svr - svl - 1. We can deal with sequence u likewise.
. The sum of numbers in the interval [l, r] would then be svr - svl - 1. We can deal with sequence u likewise.
Preprocessing takes O(n) time, and answering a query is only O(1). The total complexity would be  .
.
Solution: 6713020
Div. 2 C / Div. 1 A — Ryouko's Memory Note
Suppose we're merging page x to page y. Obviously page x should be an element of sequence a, otherwise merging would have no effect. Enumerate all possible values of x, and denote sequence b as the elements of a that are adjacent to an element with value x. If one element is adjacent to two elements with value x, it should appear twice in b. However, if one element itself is x, it should not appear in b.
For example, suppose we have a = {2, 2, 4, 1, 2, 1, 2, 3, 1}, then sequence b for x = 2 would be b = {4, 1, 1, 1, 3}, where the 6-th element appears twice.
Problem remains for finding a optimum value for y. Let m be the length of sequence b. When merging x to y, the change in answer would be
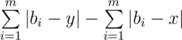
We only care about the left part, as the right part has nothing to do with y. We can change our problem to the following:
- Given n numbers on the number axis, find a number x so that the sum of the distance between x and the n given numbers is minimum.
This is, however, a classic problem. We have the following conclusion:
- The number x in the problem should be the median of the n numbers.
Proof:
Consider the case where n is odd. Proof is similar for cases where n is even.
We choose an arbitary number as x. Suppose there are l numbers on the left of x, and r numbers on the right of x. If x is the median, then l = r, so what we're going to prove is that optimal answer cannot be achieved when l ≠ r.
Suppose l < r, consider what would happen to the answer if we add d(d > 0) to x (Here we assume that adding d to x does not affect the values of l and r). The distance between x and all the numbers on the right would decrease by d, while the distance between x and all numbers on the left would increase by d. So the answer would decrease by (r - l)d, which is a positive value, since l < r.
So x would keep increasing until l = r, when optimal answer can be achieved. Thus x is the median of the n numbers.
This brings us to our solution. Simply sort sequence b and find its median, then calculate the answer. The final answer would be the optimal one from all possible values of x. The complexity is  , as the sum of the length of all b sequences does not exceed 2n.
, as the sum of the length of all b sequences does not exceed 2n.
About the pretests: Pretests for this problem are deliberately made weak, in order to make hacking more fun. None of the pretests contains adjacent numbers with the same value.
Div. 2 D / Div. 1 B — Nanami's Digital Board
Consider a similar problem: find the maximum light-block of the whole board. Constraints to this problem are the same as the original problem, but with no further operations.
A brute-force idea would be to enumerate all four edges of the block, checking can be done with two-dimensional prefix sums, so the time complexity is O(n4). Obviously it would receive a TLE verdict.
Why should we enumerate all four edges? Let's enumerate the lower- and upper-edge, and now our problem is only one-dimensional, which can be easily solved in O(n) time. Now our complexity is O(n3), still not fast enough.
Let's try to enumerate the lower-edge only, and now what we have is an array up[], denoting the maximum "height" of each column. To be specific, suppose the lower-edge is row x, then up[i] is the maximum value such that (x, i), (x - 1, i), ..., (x - up[i] + 1, i) are all light. If we choose columns l and r as the left- and right-edge, then the area of the maximum light-block with these three sides fixed would be
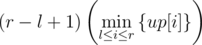
Let  , what if we enumerate h, and find the leftmost l and the rightmost r? To be more specific, we enumerate a column p, and let the height of this column be the height of the block. Now we want to "stretch" the left and right sides of the block, so we're looking for the leftmost column l such that
, what if we enumerate h, and find the leftmost l and the rightmost r? To be more specific, we enumerate a column p, and let the height of this column be the height of the block. Now we want to "stretch" the left and right sides of the block, so we're looking for the leftmost column l such that 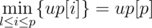 . Similarly look for the rightmost column r, then the maximum light block with its lower-edge and a point in the upper-edge fixed would be (r - l + 1)·up[p].
. Similarly look for the rightmost column r, then the maximum light block with its lower-edge and a point in the upper-edge fixed would be (r - l + 1)·up[p].
This approach can be optimized with disjoint-set unions (abbr. DSU). Imagine that initially the up[] array is empty. Let's add the elements of up[] one by one, from the largest to the smallest. Maintain two DSUs, and denote them as L and R.When we add an element up[i], set the father of i as i + 1 in R, so that i will be "skipped" during the "find" operation of DSU. Similarly set the father of i as i - 1 in L. Simply find the root of i in L and R, and we would have l and r.
Now this problem can be solved in quasi-quadratic time. We can actually further optimize it to quadratic time using monotonic queues, but we'll not talk about it here. Let's go back to the original problem.
Suppose there are no modifications, operations only contain queries. Then we could simply maintain the up[] array of every row, and similarly maintain down[], left[] and right[] arrays. Use the approach described above to achieve quasi-linear time for the answering of a query.
Now consider modifications. Modification of a single pixel only changes the values of O(n + m) positions of the arrays. So modifications can be handled in linear time.
The total complexity for the algorithm is O(n2 + qn·α(n)), where α(n) is the inverse of the Ackermann function, which is often seen in the analysis of the time complexity of DSUs.
Div. 2 E / Div. 1 C — Tachibana Kanade's Tofu
A straightforward brute-force idea would be to enumerate all numbers in the interval [l, r], and count how many of them have a value greater than k. This approach is way too slow, but nevertheless let's try optimizing it first.
The enumeration part seems hard to optimize, so let's consider what is the fastest way of calculating the value of a string. This is a classic problem that can be solved using an Aho-Corasick automaton (abbr. ACA). Build an ACA with the given number strings, and simply "walk" in the automaton according to the string to be calculated.
Consider a common method when dealing with digits — split the interval [l, r] into two, [1, r] minus [1, l - 1]. Then use DP to solve an interval, take [1, r] for instance. Consider filling in the numbers one by one, we need to record in the states of the DP the position in the string, and a flag denoting whether we're "walking on the edge of the upper bound", that is, whether the numbers we've filled are the prefix of the upper-bound r.
How can we use the approach above in this problem? Can we combine this approach with our ACA? The answer is yes, further record in the states of the DP the ID of the node we're currently "standing on" in the ACA. Consider the transfer of this DP, enumerate which number we're going to fill in, and check using our flag if the current number will be greater than the upper-bound. Appending a number to the end of our string would result in a change of the ID of the node in our ACA, so "walk" along the transferring edge in the ACA.
What about the limit of values? Simply record the current value in our DP state, during transfer, add the value stored in the ACA's node to the value stored in our state.
The tricky bit is the leading zeros. Numbers can't have leading zeros, but number strings can. How can we distinguish leading zeros from zeros in the middle of the number? We keep another flag, denoting whether we're still dealing with leading zeros.
So finally our state looks like f[len][node][val][upper_bound_flag][leading_zero_flag], where len, node, and val are current length of number, ID of current node in ACA, and current value of number respectively. Let N be the total length of all number string, and L be the length of r, the total complexity would be O(NLkm), since the number of states is O(NLk) and transfer takes O(m) time.
Solution for the approach above: 6712934 Solution for a different approach: 6713013
Div. 1 D — Nanami's Power Plant
We can use a flow network to solve the problem.
For each variable xi, create ri - li + 2 points, and denote them as node(i, li - 1) to node(i, ri). Edges are as follows:
- Link source to each node(i, li - 1) with capacity of infinity.
- Link each node(i, ri) to sink with capacity of infinity.
- Link each node(i, x - 1) to node(i, x) with capacity of MAX - fi(x). Here MAX is a number greater than every possible value of the variables.
Let C be the value of the minimum cut of this network. If there are no further restrictions, it is obvious that MAX·n - C is the maximum profit.
Now consider the restrictions. Suppose a restriction is xu ≤ xv + d, then for each node(u, x), link it to node(v, x - d) (if exists) with a capacity of infinity. If there exists a solution, MAX·n - C will be the optimal profit.
We want to prove that the edges with infinite capacity can really restrict our choice of values for variables. Note that a valid solution is correspondent to a cut of the graph. It can be proved that if a restriction is not satisfied, there will be a augmenting path in the graph. You can verify this by drawing the graphs. And because we are looking for the minimum cut, in this case the maximum sum, there can be no valid solution with a greater sum.
About the time limit: The time limit for this problem is 5 seconds, which is by far greater than this solution actually need. We set the time limit to 5 seconds because of possible worst-case complexity of the maximum flow algorithm, although in "real-life" cases that complexity is never achieved.
About the solution: This solution takes advantage of the fact that there are few possible values for the variables. And also the fact that functions are all quadratic is no use here, so statements may be quite misleading. If you have any ideas on how to solve the problem with a larger range for variables, or a solution using the fact that functions are quadratic, please share it in the comments :)
Div. 1 E — Furukawa Nagisa's Tree
In order not to mess things up, we use capital letters X, Y and K to denote the values in the original problem.
First, we can build a directed graph with n2 edges. Let E(i, j) be the edge from node i to node j. If path (i, j) is good, the color of E(i, j) is 0, otherwise it is 1.
We want to calculate the number of triplets (i, j, k) that satisfies (i, j), (j, k) and (i, k) are all good or all not good. It equals the number of directed triangles, the color of whose three edges are the same. (The triangle is like: 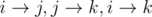 )
)
Calculating this is difficult, so let us calculate the number of directed triangles whose three edges are not all the same.
Let in0[i] be the number of in-edges of node i whose color is 0. Similarly define in1[i], out0[i], out1[i]. Let
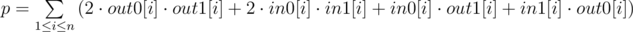
We can see that the answer is twice the number of triangles whose three edges are not all the same. So we can see the answer of the original problem is n3 - p / 2.
It's certain that out0[i] + out1[i] = in0[i] + in1[i] = n, so we only need to calculate out0 and in0.
Let us calculate out0 first. We can use the "Divide and Conquer on trees" algorithm to solve this in 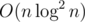 time. Choose a root i and get its subtree, we can get all the values of the paths from a node in the subtree to node i. We save the values and the lengths of the paths.
time. Choose a root i and get its subtree, we can get all the values of the paths from a node in the subtree to node i. We save the values and the lengths of the paths.
For a path from node j with value v and length l, we want to find a node k which makes G(S(j, k)) ≡ X (mod Y). Let H(i, j) be the sequence of the value of nodes on (i, j) except node i, then
G(S(j, k)) = G(S(j, i)) + G(H(i, k))·Kl = v + G(H(i, k))·Kl
As (v + G(H(i, k))·Kl) ≡ X (mod Y), so G(H(i, k)) = (X - v) / Kl. As Y is a prime number, we can get (x - v) / Kl easily. Let z = (x - v) / Kl, then the problem becomes that we need to calculate how many paths from node i to a node in the subtree except node i, whose value is z, this can be done by doing binary search on a sorted array. So we can get out0, and in0 likewise.
With these two arrays we can calculate the answer. The total complexity is 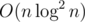 .
.











We will finish it soon
It's a bit confusing that the x coordinate is up/down while the y coordinate is left/right :p
What is this meme called?
Well, it came from a russian TV show, so i don't think that it's popular anywhere outside of CIS.
My solution for problem C only fails at test 37. Is there something special about it?
I don't know... the data is random...
My solution for Div2 Problem C fails for Testcase 30. I used the same algorithm as described in the editorial. Where could I be wrong?
Why is your
maximuminitialized as -1234567?Changed
maximumto0and added a special condition for m<=2. Accepted :) Thanks.hey my solution for this question is giving wa for testcase 20. I have checked some other's people solution and i think i have done the same thing...
Problem В:
We can actually solve the query in a linear time without any monotonic queues. We just have to notice that we are now searching not for maximum-square block, but a maximum-square block that touches a given point.
Assume we have height array for each of the four directions from the target pixel and we want to find the maximum-square block touching the X coordinate in this array.
Let's loop through the height of maximum block and move pointers to the left and right side of the block until they reach some column where height is less than the current limit. Each time we do this, let's update the maximum square. Initial positions of the pointers is X, of course.
Here is code for better understanding:
Nice approach :)
This is really cool!
Brilliant approarch. So quick and easy. This solution works O(n*m+q*n) in worst case!
wonderful!
Problem B java time limit problem Hey can body explain me the reason of such a great time difference between two java solutions. Logic is same in both, I/O is also same. http://codeforces.com/contest/433/submission/6702840 http://codeforces.com/contest/433/submission/6702752
first sol. ran in 763 ms second sol. ran in 2000 ms.
Plz i am not able to find the reason.
Arrays.sort() in Java works in O(N^2) for primitive types, so for n = 10^5 it just exceedes the Time Limit.
Hey thanks for your help, but I don't understand why java does like this?. I mean is there is any benefit in O(n^2) for primitive types.
Hi Miras321, I have searched on net, about it. But documentation says it takes O(nlogn).
docs.oracle.com/javase/7/docs/api/java/util/Arrays.html#sort(int[], int, int)
Arrays.sort() in Java works in O(n*log(n)) by using quicksort for primitive types and by mergesort for other types. So you have met with antiquicksort test. I heart about this problem year ago or more.
In Problem B, my code is getting TLE for input size of 88888 (Test Case 46), whereas it is running perfectly for input size of 100000. If Arrays.sort() is a bottleneck then how larger input size is running successfully?
http://codeforces.com/contest/433/submission/6703310
Arrays.sort on primitive types in Java 7 has worst case O(n^2) and on others is an O(n log n) mergesort. So in case 46 it has complexity of O(n^2)... while in other cases complexity is O(nlogn).
Yep, my solution was getting TLE on 46 until I forced merge sort — then it completed in (180 mills!!!) first time I see quick sort degrading in the real life — I am wondering — was it crafted on purpose??? If so — shame...
Can anyone explain in Problem C , why an obvious choice for y will be from set b only why not some other element ?
It is explained in the proof part of the conclusion I mentioned.
Thanks I read it again and got it !!!!! Very nice explanation.
Is it just me or is the statement for problem E misleading? It tells us to count triplets for which the assumption is correct. However, if the paths from p1 to p2 and from p2 to p3 belong to different players, the implication is still true.
I agree, it should be clearer.
I think "link it to node(y, x - d)" in Div 1 D should be " link it to node(v, x - d)". And I think it's quite similar to srm 590 hard.
Sorry, it's a typo... Now it's fixed... It is true that these two problems share the same idea for the model...
My solution is O(n^2 + qn) with maksay's trick.
It runs 2.361s with pypy on a random 1000,1000,1000 test set.
Unfortunately it is more than 10 times slower with python2.7 and 15 times slower with python3, which are the only ones available on codeforces :(
I really love this round, with all the anime references specially clannad and angel beats ! Makes me wanna solve all these problems, people should really do this more often, thank you very much for this :)
Glad you liked it :)
" Let , what if we enumerate h, and find the leftmost l and the rightmost r? To be more specific, we enumerate a column p, and let the height of this column be the height of the block. Now we want to "stretch" the left and right sides of the block, so we're looking for the leftmost column l such that . Similarly look for the rightmost column r, then the maximum light block with its lower-edge and a point in the upper-edge fixed would be (r - l + 1)·up[p]."
I fully disagree with this approach. It doesn't work at all. Antisample:
up = { 2 , 3 , 2 } and p=2. This approarch will answer l=r=2, so ans=3. But ans=6.
Upd: Sorry I am wrong. ans=3 not 6. Everything is clear now. It's still O(n^3) without optimizations.
I guess what he meant by enumerate is do that for every column p (not only one particular column) and for every of those rectangles check if it covers our cell. At least that's how I did it.
Can anyone please briefly explain how can we solve Problem A using Knapsack DP?
Let f be a two-dimensional boolean array, f[i][j] is true iff we can choose a subset of the first i apples such that the sum of their weights is j. Initially only f[0][0] is true. Consider adding the i-th apple, if f[i - 1][j] is true, then certainly f[i][j + weighti] should be true. This way we can know all the values of , if f[n][sum_of_weights / 2] if true, then the answer is "YES", otherwise "NO".
, if f[n][sum_of_weights / 2] if true, then the answer is "YES", otherwise "NO".
Thanks very much, for the explanation !
Did someone manage to solve problem E? There is no link to the solution in the editorial, and the explanation is very vague. It seems that nobody managed to solve it so far, or is it just an ongoing problem with the testing system?
Also, what is "Judgement failed"? My submission passed all tests and I got this. And now I can't resubmit it because "You have submitted exactly the same code before". Awesome..
Your solution probably passed the pretests, but not the real tests. The real tests are only run after the competition has finished.
I didn't take part in the contest (it was too early in the morning), but submitted it afterwards as practice. It shows all (?) 36 tests as passed. http://codeforces.com/contest/434/submission/6707377
It says "Accepted", no?
It does now. Apparently they had issues yesterday.
The link to your submission is for problem Div 1 D, not E...
I know, there are two parts in my post.
When I click the solution: "You are not allowed to view the requested page"?
Can you fix it? :D
Sorry about that, now it's fixed :)
"If one element is adjacent to two elements with value x, it should appear twice in b",
I'm sorry huzecong, but I didn't understand the reason for that. Could you explain me? or Anybody?
Thanks
if you change the value of x , the element will be affected twice
Thank you Shana!
If I had, a = [1 2 2 4 5], can I merge 4 2 or only 2 4?
both you can have [1 2 2 2 5] or [1 4 4 4 5]
Do we really need knapsack DP for Div.2 A problem? This got accepted: http://codeforces.com/contest/433/submission/6730272
Of course not, I was just talking about an alternative solution.
I think that there is a mistake in the solution described above to Div1 E. In my opinion, the value of p should be
Look at the figures below to see why.
The two types of situations will simultaneously lead two triangles to be illegal .
And the two situations below will only lead one triangle to be illegal.
So the coefficients should be 2 2 1 1 instead of 1 1 1 1.
I think it is just a careless mistake made by the author.
You're right... Now the editorial is fixed, thank you for your correction!
hii huzecong, In your solution to this problem, you are calculating the answer as (cout << sum / 2 — ans << endl;). I do not get the approach behind it.
Because the absolute difference between every pair of adjacent numbers is calculated twice in
sum. Hereansis the maximum value that could be substracted due to merging.