I'm sorry about my poor English. And I made a mistake that I reverse $$$n$$$ and $$$m$$$. In this blog, $$$n\le 10^5$$$, $$$m\le 10$$$, $$$1\le l\le r\le n$$$.

This is a online determined algorithm.

First, make every cross a vertex. Give each vertex a position $$$(x, y)$$$. The position of a vertex equals to the position of the character on its right down side. There is an edge between two vertexes if and only if $$$|x_1-x_2|+|y_1-y_2|=1$$$ and the edge splits two different characters.

If a vertex doesn't have any edge, remove it.

For example, for the example situation in the problem.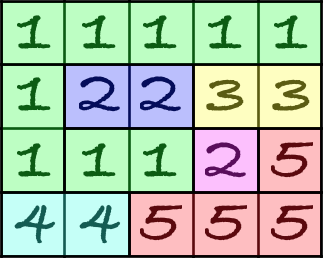

We will get the graph: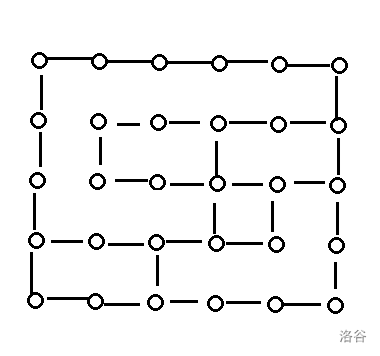

When calculating the answer of a range $$$[l,r]$$$, it is just like adding edges at the column of $$$x=l$$$, the column of $$$x=r+1$$$, and removing all the edges out of $$$[l,r+1]$$$. For example, we need to calculate the answer in range $$$[2,4]$$$ in the previous graph. We just need to calculate the number of "faces" in the remaining graph.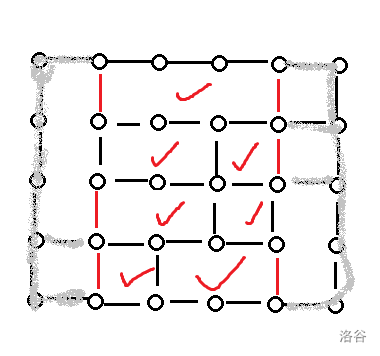

Define F as the number of faces(excluding the outside face), E as the number of edges, V as the number of vertexes. Then:
Lemma 1: $$$V-E+F=1$$$ holds for each connected planar graph.

For any planar graph, make summation for both sides of $$$V-E+F=1$$$ between different connected blocks. We get $$$\sum V_i -\sum E_i + \sum F_i = \sum 1$$$, means $$$V-E+F=C$$$, where $$$C$$$ is the number of connected blocks.
In order to find the value of $$$F$$$, we can find the values of $$$V,E,C$$$.

Define $$$V_i$$$ as the number of vertexes with just right $$$i$$$ degree(s). From the rule of building the graph, we can find that only $$$i\in {2,3,4}$$$, can $$$V_i>0$$$. $$$F=E-V+C$$$, so $$$F=E-V_2-V_3-V_4+C$$$. Notice that one edge contributes two degrees. So $$$E=\frac{\sum_i iV_i}{2}$$$ holds for any graph. For our planar graph, $$$F=\frac{2V_2+3V_3+4V_4}{2}-V_2-V_3-V_4+C$$$ holds. It equals to $$$F=\frac{V_3+2V_4}{2}+C$$$.

There won't be any vertexes with $$$4$$$ degrees on the any side of the range because all edges outboard are removed.
We can get the prefix sum in row to calc the sum of $$$V_3+2V_4$$$ in each column. On the both sides, each pair of different adjacent characters causes a vertex with $$$3$$$ degrees, so we can the sum of each column.
Then $$$\frac{V_3+2V_4}{2}$$$ can be calculated in $$$\mathcal{O}(1)$$$ steps for each query.

For a connected block in the cut graph, it can either be connected with the edges added, or be independent. The number of the former is always $$$1$$$. For the latter, each block MUST be an independent connected block in the original graph. If it takes vertexes from $$$x=l_0$$$ to $$$x=r_0$$$, when the query is $$$[l,r]$$$, it can be independent if and only if both $$$l<l_0$$$ and $$$r>r_0$$$ hold.

We can dfs to find all the connected blocks in the original graph. There will be several pairs $$$(l_i,r_i)$$$, describing one block each pair.
You can use segment tree to solve it offline with $$$\mathcal{O}(\log q + \log n)$$$ steps each query.

Lemma 2: $$$\sum_i(r_i-l_i+1)=\mathcal{O}(nm)$$$.

Consider that $$$\sum_i [l<l_i<=r_i<r]=\frac{1}{2}\sum_i ([l<l_i<r]+[l<r_i<r]-[l_i\le l<r_i]-[l_i<r\le r_i]+2[l_i\le l\le r\le r_i])$$$. It is easy to calculate first four items in $$$\mathcal{O}(1)$$$ for each query with prefix sum algorithm.

We can treat segment information as binary numbers. We can create a sequence $$$f$$$ with $$$n+1$$$ numbers, and with $$$\mathcal{O}(m)$$$ bits in each number(it can be proved that it is enough to have $$$m$$$ bits each). Then, we distribute a $$$p_i$$$ to each $$$(l_i,r_i)$$$, satisfies $$$\forall r_i+1=l_j, p_i\neq p_j$$$. Then we set the $$$p_i$$$-th bit of the $$$x$$$-th number to $$$1$$$ for all the $$$l_i\le x\le r_i$$$. We can do this one-by-one by the limit of $$$\sum_i r_i-l_i+1$$$. Concretely, we can use bucket sort to sort $$$(l_i,r_i)$$$ to make $$$l_i$$$ non-decrease in $$$\mathcal{O}(n)$$$ steps. Then solve from left to right, record bits are taken in $$$2$$$ columns before and bits are not.

There is an $$$i$$$ satisfies $$$l_i\le l\le r\le r_i$$$ if and only if $$$\forall l\le j\le r, f_{j,p_i}$$$ is $$$1$$$. In the other hand, the number of $$$i$$$ satisfies $$$l_i\le l\le r\le r_i$$$ equals to $$$\operatorname{popcount}(\large \operatorname{and} _{i=l}^{r} \normalsize f_i)$$$.

We just need a data structure to maintain a sequence $$${a_n}$$$ satisfies $$$0\le a_i\le 2^m$$$, with $$$\mathcal{O}(nm)$$$ steps preprocess and $$$\mathcal{O}(1)$$$ steps to calculate the bitwise and sum of a range.
Fortunately, there is a data structure called sqrt tree, can solve the problem in $$$O(n\log \log n)$$$ — $$$O(1)$$$ steps. So, when $$$m>\log \log n$$$, the problem is solved.

To solve situations $$$m$$$ is small, we can divide the sequence into blocks. The length of each block is $$$b$$$. The situations of numbers in one block cannot over $$$2^{mb}$$$. We can compress numbers in a block into one number, and create a table, reflect situations to the and sum. The preprocess has $$$\mathcal{O}(2^mb)$$$ steps.

When the query is $$$[l, r]$$$, we actually calculate the and sum of $$$[l,cb],[cb+1,(c+1)b+1],\dots,[db+1,r]$$$. We build a sqrt tree for a sequence $$$g$$$ that $$$g_i=\large \operatorname{and} _{j=(i-1)b+1}^{ib} \normalsize f_i$$$. The length of $$$g$$$ is $$$\frac{n}{b}$$$, and the preprocess has $$$\mathcal{O}(\frac{n}{b}\log \log\frac{n}{b})$$$ not over $$$\mathcal{O}(\frac{n}{b}\log\log n)$$$. Dividing $$$l$$$ and $$$r$$$ by $$$b$$$ helps us get $$$c$$$ and $$$d$$$ in $$$\mathcal{O(1)}$$$.
When we calculating the and sum of $$$[l,cb]$$$, we can bitwise or $$$g_c$$$ with $$$2^{bm}-2^{(cb-l+1)m}$$$, such that $$$a_i$$$ satisfies $$$(c-1)b\le i<l$$$ has no influence on the result. Because of the bitwise operations, the process just need $$$\mathcal{O}(1)$$$ steps. In the same way we can calculate $$$[db+1, r]$$$.

The time complexity of the data structure is $$$\mathcal{O}(\frac{n}{b}\log\log n+2^{mb})$$$ — $$$\mathcal{O}(1)$$$. When $$$m<\frac{\log n}{\log\log n}$$$, we get $$$b=\log\log n$$$ that $$$\mathcal{O}(\frac{n}{b}\log\log n+2^{mb})$$$ is no more than $$$\mathcal{O}(n)$$$, obviously less than $$$\mathcal{O}(nm)$$$.

So we solved 811E or #416 E in $$$\mathcal{O}(nm+q)$$$, and the algorithm is online.

Accepted Code