Problem : Link
In a race there are n horses. You have to output the number of ways the race can finish. Note that, more than one horse may get the same position. For example, 2 horses can finish in 3 ways. - - Both first - horse1 first and horse2 second - horse2 first and horse1 second
My Idea is just Count all the way , there are two case when position are same or position increment of horse.
ans= solve(pos,h+1)+solve(pos+1,h+1)
But it fails , But Why ?
Can anyone explain why my idea fail and describe about the idea above or give a solution idea .
Thanks in advanced :)











It might be failing because of integer overflow. If they're asking you to compute the result modulo 10056, it means that the result will probably be huge (even bigger than the biggest
long longinteger).You must use this fact: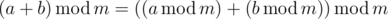 , assuming that
, assuming that  is the classic
is the classic
%operator in C/C++. This way you won't exceed integer's capacity.Thanks :)
Cool problem! You need to consider combinations, I think that's why your idea fails. Let me break down case
n = 3, hopefully you'll see the recurrence:Everyone comes in 1st: clearly order doesn't matter, so just add 1 to your answer.
Two guys come in 1st: could be (1, 2), (1, 3), or (2, 3) -that is combinations of 3 elements picked 2 at a time. The other guy can only be 3, 2, or 1 correspondingly, so add (3 * 1) to the answer.
1 guy wins: must be 1, 2, or 3 (comb. of 3 elements picked 1 at a time)! What happens to the remaining positions? They could have tied, or one guy beat the other... But hey, isn't that case
n = 2(which you described in your example)! So, add to the solution (3 * 3).Hope that helped!
Thanks ur explanations are great help :)
Simply put DP: let P[n] denote the number of ways n horses could finish the race; all operations will be done mod m.
Out of n horses, any 1 ≤ k ≤ n could've taken first place; the number of ways to choose k horses is . The remaining n - k horses finished in 2nd..x-th place, which is the same as a result of a race with n - k horses. Therefore, we get a recurrence relation
. The remaining n - k horses finished in 2nd..x-th place, which is the same as a result of a race with n - k horses. Therefore, we get a recurrence relation
with $P[0]=1$.
I get that , thanks for ur help :)