Codeforces Round #260 — Editorial

#	User	Rating
1	MiFaFaOvO	3520
2	tourist	3461
3	Um_nik	3367
4	apiadu	3351
5	mnbvmar	3332
6	Benq	3330
7	LHiC	3276
8	TLE	3271
9	Radewoosh	3251
10	ecnerwala	3241

#	User	Contrib.
1	antontrygubO_o	189
2	Errichto	187
3	tourist	181
4	Radewoosh	173
5	vovuh	166
5	pikmike	166
7	ko_osaga	162
8	Um_nik	160
9	rng_58	155
10	Petr	154

Warning: my English is very bad.

Solution: 7407613;

In this task you need to check the existense of such pair i and j, such that i ≠ j, a[i] < a[j], b[i] > b[j]. If such i and j exist, Alex is happy.

There is very simple solution. Let's check that for all i a[i] = b[i]. If this condition is true we should print "Poor Alex". We can easy prove it. Let's sort arrays a and b like pair of numbers in increasing order. We can see that Alex is happy if we have at least one inversion in array b, i.e there is such pair i and j that b[i] > b[j] и i < j (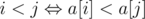 $\text{[math]}$ ). i.e it means that array b is not sorted and it's means that a ≠ b.

456B - Fedya and Maths

Solutions: 7407625, 7407631;

In this task you need to calculate formula that given in the statement, but it's hard to calculate it with the naive way.

But we can transform our formula to this:

$\text{[math]}$

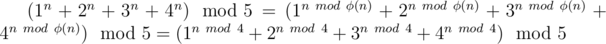
This formula is right because 5 is prime number and it's coprime with 1, 2, 3, 4.

φ(5) = 4

To solve this task we should be able to calculate remainder of division n by 4 and calculate formula for small n.

Asymptotics — $\text{[math]}$ .

There is also another solution. It uses a fast exponentiation, but not binary exponentiation. The idea of this exponentiation is the same as that of the binary exponentiation. Let we want to fast calculate xⁿmodP. Algorithm is very simple. Let process digits of n moving from end to begin. Let Result — current result and K — x^(10ⁱ), i — number of the currently processed digit (digits are numbered from the end. Used 0-indexation). During processing of digits, we must update result: 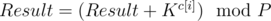$\text{[math]}$ , c[i] — i-th digit of the number n (digits are numbered from the end).

Asymptotics — $\text{[math]}$ .

456C - Boredom / 455A - Boredom

Solutions: 7407649, 7407655;

In this task we need to maximize the sum of numbers that we took. Let precalc array cnt. cnt[x] — number of integers x in array a. Now we can easily calculate the DP:

f(i) = max(f(i - 1), f(i - 2) + cnt[i]·i), 2 ≤ i ≤ n;

f(1) = cnt[1];

f(0) = 0;

The answer is f(n).

Asymptotics — O(n).

456D - A Lot of Games / 455B - A Lot of Games

Solutions: 7407663, 7407670;

To solve this problem we need the prefix tree(trie), which will have all the strings from the group. Next we will calculate the two DP: win[v] — Can player win if he makes a move now (players have word equal to prefix v in the prefix tree(trie)). lose[v] — Can player lose if he makes a move now (players have word equal to prefix v in the prefix tree(trie)).

if v is leaf of trie, then win[v] = false; lose[v] = true;

Else win[v] = (win[v] or (not win[i])); lose[v] = (lose[v] or (not lose[i])), such i — children of vertex v.

Let's look at a few cases:

If win[v] = false, then second player win (first player lose all games).

If win[v] = true и lose[v] = true, then first player win (he can change the state of the game in his favor).

If win[v] = true and lose[v] = false, then if 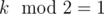$\text{[math]}$ , then first player win, else second player win.

Asymptotics — 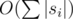$\text{[math]}$ .

456E - Civilization / 455C - Civilization

Solutions: 7407681, 7407683;

You can see that the road system is a forest. For efficient storage component we need to use DSU. First, we need to build the initial system of roads. For each component of the initial road system, we must find the diameter of component. This can be done using a DFS or BFS. Let a — any vertex of component. Let b — furthest vertex from vertex a. Let c — furthest vertex from vertex b. Diameter equal to distance from b to c. This algorithm for finding the diameter is correct only for tree. For each component in the DSU, we know its diameter.

Now it is very easy to answer the query of the $1$st type: To know the component which contains the vertex x and output diameter of this component. Query of the $2$nd type also very easy to process: Let u — of component in which lie the vertex x, v — of component in which lie the vertex y. If u ≠ v, then we can merge components: The diameter of the new component is computed as follows:

$\text{[math]}$

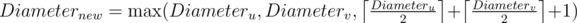
Asymptotics — O(n·A^- 1(n)), где A^- 1(n) — inverse Ackermann function.

455D - Serega and Fun

Solutions: 7407693, 7407699, 7407703;

Let's change the query type 1 to two more simple requests:

Erase a number from r-th position. Insert this number after (l - 1)-th position.

Now let's keep our array as $\text{[math]}$ blocks. In each block will store the numbers themselves in such a manner as in the array a and will store an array cnt. cnt[x] — number of integers x in block. This requires O(n sqrtn) space.

Now we can fast process the queries of the 1st type. We can erase number from r-th position in 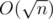$\text{[math]}$ operations. And we can insert this number after (l - 1)-th position in 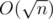$\text{[math]}$ operations. Also we can fast recalc cnt after transformations.

Also we can fast process the queries of the

Unable to parse markup [type=CF_TEX]

O (\ sqrt n) $ numbers are in blocks, which are partly lie within the boundaries of the query.

To keep the size of the blocks close to $\text{[math]}$ , we need rebuild our structure after each 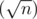$\text{[math]}$ -th query of the 1st type. We can rebuild structure in O(n) operations.

Asymptotics — 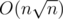$\text{[math]}$ .

455E - Function

Solutions: 7407711, 7452418;

In this problem you should quickly be able to compute the function described in the statement.

You may notice that this task is equivalent to next task:

Go through the array a, starting from the position of y, making (x - 1) step. Step might be: step to the left or to stay in place.

Function is calculated as follows: 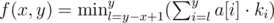$\text{[math]}$ , k_i — how many times we visited the i th element of the array a.

For a fixed l is clear, it is most optimally that a minimum on the interval [l, y] has been visited by (x - (y - l)) times, and all the other numbers once.

You may notice that optimally to a[l] was a minimum.

From all this we can conclude that for a fixed l answer is — sum[y] - sum[l] + a[l]·(x - (y - l)), where sum — an array of prefix sums of array a.

Above formula can be written as follows:

sum[y] - sum[l] + a[l]·(x - (y - l)) = sum[y] - sum[l] + a[l]·(x - y + l) = sum[y] - sum[l] + a[l]·l + a[l]·(x - y) = sum[y] + (a[l]·(x - y) + a[l]·l - sum[l])

You may notice that in brackets something like the equation of the line — K·X + B. That's very similar to the equation of the line: a[l]·(x - y) + a[l]·l - sum[l], where K = a[l], X = (x - y), B = a[l]·l - sum[l].

Now we must find minimum for all l and fixed X = (x - y).

We have n lines, i. e. for every element in array a one line (K_i, B_i).

Answer for query equal to:

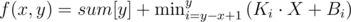$\text{[math]}$ , where (K_i, B_i) — i-th line. K_i = a[i], B_i = a[i]·i - sum[i].

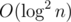For fast answer calculation we must use Convex Hull Trick with segment tree. In every vertex of segment tree we keep all lines for segment of this vertex. This requires $\text{[math]}$ space, because each line lies in $\text{[math]}$ vertices. And we can answer query in $\text{[math]}$ operations. Because we visit $\text{[math]}$ vertices and each vertex need in $\text{[math]}$ operations. You can learn the theory about Convex Hull Trick here.

// Array of nodes. If trie[i].next[x] is 0, then there is no path with // character x from the node i. Otherwise it is an index of the next // node. struct trie_node { int data; int next[26]; }; trie_node trie[100005]; // Number of allocated nodes, 1 by default for trie root int count = 1; void insert(const string& s) { int p = 0; // Index of the current node, 0 by default for root for (char c : s) { int x = c - 'a'; if (trie[p].next[x] == 0) { // This is a leaf, attach new node to it. // For new node, take trie[count], and increase count. trie[p].next[x] = count++; } // Advance to the next node p = trie[p].next[x]; } trie[p].data++; }

void insert(int pos, int value) { // We traverse all blocks for (int block_id = 1; block_id <= numberOfBlocks; block_id++) { if (all[block_id].size() < pos) { /* if this block is smaller than the position we need, then we skip this block and decrease our pos by block's size */ pos -= all[block_id].size(); } else { /* when we found a block where our pos is located, we just insert needed value */ cnt[block_id][value]++; all[block_id].insert(all[block_id].begin() + pos, value); return; } } }

void reBuild() { vector<int> arr; // our array // first, clear all information about blocks for (int i = 1; i <= numberOfBlocks; i++) { for (auto it : all[i]) { cnt[i][it] = 0; arr.push_back(it); } all[i].clear(); } int ptr = 1; for (int i = 1; i <= n; i++) { /* just add each element one by one, once some block is full, move to the next one */ all[ptr].pb(a[i]); cnt[ptr][a[i]]++; if (all[ptr].size() == blockSize) ptr++; } }

#include <bits/stdc++.h> using namespace std; bool cmp_pair(pair<int, int> a, pair<int, int> b) { return a.second > b.second; } int main() { int n; cin>>n; vector<pair<int, int>> vec; while (n--){ int a, b; cin>>a>>b; vec.push_back({a, b}); } sort(vec.begin(), vec.end()); cout<<(is_sorted(vec.begin(), vec.end(), cmp_pair)? "Happy Alex":"Poor Alex"); return 0; }

Comments (107)

Write comment?

MinakoKojima

5 years ago, # |

← Rev. 14 →

+42

Problem D could be solve by Splay which invented by Darooha in O(nlog²n) without the ungraceful $\text{[math]}$ part.

It is hard to answer the query if you only have one Splay. The key point is to build more splays with each different k (k-splay). Let's call the splay with all elements 0-splay.

Thus, for query, you can find the interval of [l, r] on the k-splay by a variation of select() function. The different of it between the regular is not use rank of the node but the rank of the corresponding node on the 0-splay.

For modification, you should also adjust the position of a node in 0-splay and the corresponding k-splay. So for each node, we add one more field to store the corresponding node in another splay.

struct node{
    node *child[2],*parent,*corresponding; 
    int size, key; 
    ...
}

Check my submission or vfleaking's for detail.

→ Reply

dezhonger

5 years ago, # ^ |

Do u know Russian?

nblt

Why is O(nlog2n) ? I think just O(nlogn) .

Fischer

21 month(s) ago, # ^ |

← Rev. 2 →

Because is a implicit treap with keys linked to nodes in others implicit treaps for all k. O.o cool. code

_Saitama_

3 years ago, # ^ |

really inspiring

hpfdf

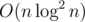My $\text{[math]}$ solution using Treap.

Any balanced tree with father pointers would work. Treap is easier to write.

R.A.X

Can anybody explain about How to implement the trie using an array instead of pointer??

Mostafa_36a2

I've used to implement tree with a 2-d array [if you guarantee 2 child for every node] the array will look like this


a
bc//b and c are the childs of a
defg//d and e are the childs of b
hijklmno//l and m are the childs of f

if you want to reach the first child of the i-th node in the j'th level : level=j+1,id=2*i

but how we can implement trie (prefix tree) using it??

Hailo

You could see my code here 7393354

Y use a trie using a vector of pairs and Grundy number to solve the game I know that my code couldn't be clear but I hope it could help you

Sorry for my english too

andreyv

← Rev. 4 →

You do it like with the standard trie, but replace pointers with array indices and node allocation with index advance:

.data is the information we want to store in tree nodes. For example, it can hold the number of strings ending in this node, like it does in the insert() function above.

As an exercise write a contains_prefix(s) function for this structure.

hzyfr

A full structure of Trie should be a more bit representing "is some word ends here"

Good point, fixed.

selfcompiler

can some one explain "how to use the convex Hull Trick with segment Tree" in DIV-1 E

mnbvmar

Remainder: convex hull trick lets us maintain k linear functions of the form f_i(x) = a_ix + b_i and answer efficiently (in time proportional to number of functions) to the queries Q(x) = min_{1 ≤ i ≤ k} f_i(x) (given x).

Now we will be able to solve the problem if we can answer a bit more general kind of queries: we consider only lines with indices from given L and R; formally, Q(x, L, R) = min_{L ≤ i ≤ R} f_i(x).

How can we do it? Let's make a segment tree! Let's say we have such m that 2^m ≥ n. Then the root contains the convex hull of lines having indices [0, 2^m - 1], its left child contains [0, 2^m - 1 - 1], right child [2^m - 1, 2^m - 1] and so on. We can costruct all these hulls one by one; without any optimizations it gives us time $\text{[math]}$ .

Now let's say we have to answer the query Q(x, L, R). Then we just "break" the interval [L, R] into base intervals (in the same way a segment tree does) and for each of $\text{[math]}$ such base intervals we find its minimum at x. Now we see that the answer is the smallest of these minima. It doesn't matter that we consider some groups of lines from interval [L, R] separately — still, we can just take the smallest of the results.

What's the time? We have $\text{[math]}$ base intervals, for each of them we can compute the answer in $\text{[math]}$ , so total time is 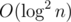$\text{[math]}$ . There are some ways which let us compute all answers off-line in $\text{[math]}$ , but it's not the subject :P

a_ix + b_i -> a_ix + b_i

@mnbvmar would you like to provide a neat and clean implimentation of convex hull Trick .It is a great help for me and naive learner's like me

caioaao

http://codeforces.com/blog/entry/8219

this topic is a great way of learning about the convex hull trick. the DS itself is ~30 lines of code, really simple if you understand geometry basics

DaneshvarA

Hi. I'm new to DP. Can someone please explain me where did the formula for problem div2 C or div1 A come from? Implementing it is not hard but I have problem with the formula. Why should f[i] be as said in the editorial? I don't understand...

I would be thankful if someone could give me more explanation about it. Thanks

A more straightforward formula looks like this

Let f[i][0] = max. answer considering numbers <= i && doesn't choose i, f[i][1] = max. answer choose i

Then f[i][0] = max(f[i-1][0],f[i-1][1]), and f[i][1] = f[i-1][0] + cnt[i]*i

Actually this is doing the same thing as the formula in editorial.

shas.atman

I am confused as to what cnt[i] is supposed to represent. What exactly does cnt[] store?

cnt[i] is the number of the times that the number i has appeared in the input list. It can be calculated while reading the input.

paulabhik47

cnt[i] represent the frequency of the number "i"

fanatique

Why are not considering the case of Ak + 1 ? Doesn't the value of f[i] depends on both f[i-1] and f[i+1]? I know, this sounds stupid with this condition but please do reply.

sumanthbharan

Shouldn't the statement be this:

dp[i][0] = dp[i - 1][1];
dp[i][1] = dp[i - 1][0] + cnt[i] * i;

Because if we don't choose i, then we definitely have to choose i-1 to remove i.

And if we have to choose i then we will have to not choose i-1 => dp[i - 1][0] and for choosing all occurrences of i we get cnt[i]*i

Any help regarding this would be greatly appreciated.

Thanks

sajalagrawal14

6 months ago, # ^ |

it is wrong , it should be dp[i][0]=i*b[i]+dp[i-1][1]; dp[i][1]=max(dp[i-1][0],dp[i-1][1]); because if you do not select i , then you have both option to choose i-1 or not and who ever is max take the ans

lunatic666

4 years ago, # ^ |

before doing boredom question try this one simpler version of boredom https://www.hackerearth.com/problem/algorithm/choosing-the-judges-7/description/

AAshmawii

Hi, If you understand this problem (Div1 A), could you explain it? because I can't understand the problem :).

RaghavN

Warning: please take this explanation with a pinch of salt, because I'm myself new to DP, and it may thus be incorrect ...

First, we pre-compute the frequency of occurrence of each element in Alex's sequence (using the array "freq", say)

dp[i] stores the maximum sum that Alex can get using the numbers from 1 to i. Thus, dp[0] is 0, and dp[1] is freq[1] (i.e., number of '1's in the sequence)

For i = 2 to 10^5 (10^5 being the maximum possible value of any number in Alex's sequence according to the given constraints), dp[i] is calculated using the inference that each set of "i"s (if at all they occur in the sequence) can either all be picked OR not picked at all:

dp[i] = max(I, II), where:

I = dp[i-1] represents the situation where "i" isn't picked at all (As "i" isn't picked at all, none of the "i-1"s will be deleted, and the sum will be the same as the one calculated for dp[i-1])

II = dp[i-2] + (freq[i] * i) represents the situation where all "i"s are picked (As all the "i"s are picked, all the "i-1"s WILL be deleted, and we cannot consider dp[i-1] at all, given that dp[i-1] was itself computed while considering the situation where all the "i-1"s may be picked. Instead, we use dp[i-2]; the sum computed therein is safe to use, given that none of the "i-2"s will be deleted when the "i"s are picked. Also, as we are picking all the "i"s, our previous sum (i.e., dp[i-2]) will increase by (freq[i] * i))

Final answer will just be dp[100000].

My implementation of the above logic (C++): http://codeforces.com/contest/456/submission/18021003

hell_hacker

Thank You for the explanation!

swimer

← Rev. 3 →

Hello.
Could you help me?
problem C div 2.
link to task
How is it possible to get 16 from this test case?
5
5 3 5 3 4
windboy hell_hacker raghavn

suraj021

First you choose 1st 3, then 4 will be deleted and score will be 3. And then 3, 5, 5 can be picked without deleting any other number, hence total score of 16.

Vicennial

Alternative way is to use a 2 dimensional dp.
dp[i][0] represents max value you can get from 1 to i and not picking i.
dp[i][1] represents max value from 1 to i and picking i.
The relations for each i are:
Base case- dp[0][0]=dp[0][1]=0;
dp[i][0]=max(dp[i-1][0],dp[i-1][1])'
dp[i][1]=freq[i]*i+dp[i-1][0];

Then answer would be max(dp[100000][0],dp[100000][1]).

I personally find that single dimensional dp can sometimes be tough to understand so I use 2d normally.

Implementation:21918844

grg124

2 months ago, # ^ |

better solution for understanding than above

better solution for understanding than all above

Laxus_Dreyar

thanks bro

kiner_shah

I have a doubt with the sample test case for Div. 2. (C) / Div. 1. (A) Boredom:

9
1 2 1 3 2 2 2 2 3

Can't the answer be more than 10?

For e.g., say if we delete first 3 which leads to score = 3 and sequence as 1 1 3 2 2 2 2. Then, again we delete 3, leading to score = 6 and sequence as 1 1 2 2 2. Then we delete 2 leading to score = 8 and sequence 1 2 2. Then continuing to delete the rest 2s, we can get score = 12.

Am I going somewhere wrong?

agnivabasak1

18 months ago, # ^ |

-8

hi ,i think you have got the question a bit wrong . if you delete 3 at first you would have to delete all the elements in the sequence which is either 2(i.e, 3-1) or 4 (i.e 3+1) , so the score =3,seq = 1 1 3. so you see ,after this the maximum you can get is by deleting each remaining element as none of them is 1 unit apart . therefore,final score =3+3 +1 +1=8. which is less than 10.

Yes, indeed! I think I, somehow, misunderstood the delete operation mentioned in the question.

anjalic2503

15 months ago, # ^ |

why there cant be a case where some i's out of the freq[i] are selected ?

nat10niel

8 months ago, # ^ |

Sorry for bringing up such an old thread, could you please explain why the final answer should be dp[100000] instead of dp[n] which is specific to the test case? Thanks

arron_tij

7 weeks ago, # ^ |

n is not specific to the test case. Look again, n is the size of the array. You are confusing it with the maximum integer of the array which would in fact be specific to the test case.

makkoncept

4 weeks ago, # ^ |

Yes, you can also say that the answer is dp[n]. In fact, dp[100000] will be equal to dp[n], because freq[i] (for i > n) will be 0 and therefore the value of dp[n] will propagate upwards to n=100000.

OmarSaber

In the tutorial of Problem 456B - Fedya and Maths

I can't really understand the transformation of the equation if anyone can explain.

speedyGonzales

Dude, check out this Euler theorem

we know from modulo theory examples : 3%5=-2%5, 4%5=-1%5 so new equation is - (1)^n+(2)^n+(3)^n+(4)^n=(1)^n+(2)^n+(-2)^n+(-1)^n - so for n==odd answer is simply "0" for n==even which are multiple of 4 answer is =4 and for n==even which is not multiple of 4 ans is zero. take a pen and paper do some work on it you can get that idea and the complexity of this solution is O(1) .

paramvi

for the problem 1, going by logic of tutorial and so many other solutions, Alex should be happy for the following data set: (2 1) (3 4) But we can see clearly, it is not so. Am I missing anything?. Thanks.

netman

Limitations: 1 ≤ a_i, b_i ≤ n. Your data set is incorrect.

DVRazor

I completely agree with you. I quite dislike the statement of the problem. It's just so not obvious that all prices and qualities are numbered from 1 to n; could be as well stated that way. Many people thought in the same way and solved a more general problem.

In the editorial of problem D div2, Consider the example 2 1 abas abacaba now the player one can win and loose the game. so win[root]=true and loose[root]=true.so according to editorial its answer should be first.But the answer is second.Let's consider these moves a--b--a--s using this prefix the player 2 will win? Can anyone explain this to me??

sergioRG

From my debug printing of my AC submission: Starting player can FORCE win? false , can FORCE lose? false Second ``

In fact, if we merge the two given strings we get something like this:

aba — s \ caba

There are only two possible games. Both share the initial "aba" prefix. The starting player must pick the second a, so the non-starting player can force a win (by choosing the "s") or a lose (by choosing the "c"). So, the starting player outcome only depends on what the non-starting one decides. In this case, we have k = 1, so the Second player can directly win. In fact, in this case the optimal strategy for the second player is winning every game, since the loser player will be the starting one.

In the test you given win[root]=false and lose[root]=false. Check that again!

Correct me if I am wrong. the above test case can be written as Let' name them:_________________________________________________________________________________ (1)a--(2)b--(3)a--(4)s _______________|_____________________________________________________ __________________(5)c--(6)a--(7)b--(8)a

Now in the 4th node

win[4]=false

win[3]=true

win[2]=false

win[1]=true

similarly

loose[8]=true

loose[7]=false

loose[6]=true

loose[5]=false

loose[4]=true

loose[3]= loose[4]|loose[5] =true

loose[2]=false

loose[1]=true

would anyone like to explain for problem E DIV-1 how we got this relation Function is calculated as follows: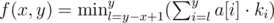 , ki — how many times we visited the i th element of the array a.

i understand it :)

netman in your code of Problem E of DIV 1 Can you explain the algorithm of function addline() and mergeCHs() ,how these function works ? it will be great help !!! sorry for my bad english

addLine() — it is adding line to Convex Hull. In my structure all lines are in decreasing order of K. And we can easily add line to structure in O(1) operations. You can draw a lines in the order of decreasing K to better understand this.

If our lines are in decreasing order of K in structure, we can easily merge 2 structures. Add all lines in decreasing order to new structure in O(n + m) operations, where n and m — sizes of 2 structures.

Read this article to better understand.

netman in your addline() function the first if condition you do this bb=max(b[l-1],bb) i did not get the idea why you did this . please explain it

Ohh... sorry... In right solution must be bb=min(b[l-1],bb).

Tests very weak and my solution with this bug passed tests :(

thinh2601

Can anyone give me detail explain for solution of problem D div 1 ?

nisargshah95

I agree. Your English is very bad :P. But can you please make someone else post in English? I cannot understand the tutorials properly. :(

sakaark

opening solution 7452418 of PROBLEM 455E — FUNCTIONS shows "you are not allowed to view the requested page". Why is that? Please fix it! Thanks

calmhandtitan

netman can you please tell what does f(i) denote in the editorial for problem C of Div2.?

f(i) — maximal sum if we delete all numbers that smaller or equal to i.

thanks :)

netman if it is so, then how would f(n) give answer to original problem, as any number lies between 1 and 10^5 and is also independent of value of n.

there could be a test case like


3
1 9 10000

So, I think the answer should be f(max(a[i])) [for all i in range(1, n)]

Please correct me if I am wrong. I am quite weak at DP.

You are right =)

Answer is f(maxA).

irajdeep

Problem D. I'm not able to understand the relation — win[v] = (win[v] or (not win[i])); lose[v] = (lose[v] or (not lose[i])), such i — children of vertex v. Can anyone explain ? Thanks

Can someone please explain 456C — Boredom / 455A — Boredom ?

According to what I understood, the above statement does the following:

f(i-1) Here the number i-1 is selected at some point number which removes all the occurrences of the number i, hence there is no term cnt[i]·i
f(i-2)+cnt[i]·i Here the number i-2 is selected at some point which removes all the occurrences of number i-1 and then we are separately removing all the occurrences of the number i which is the term cnt[i]·i
Then we are taking the maximum of the above two calculated values.

But it can be possible that we do not select the number i-1 in f(i-1) and also we do not select the number i-2 in f(i-2).

So how is this correct? Any help would be greatly appreciated.

radoslav11

Lets say that the numbers are contained in an array of srtucts a[], and it is sorted by the number in it.

That struct contains the current number and time it is writen.

The idea is that there is no sense to chose f(i-2), without chosing "i" too, because all numbers are >= 0. So we will either chose the current (ith) number or we will skip it. That means if(a[i-1].numb == a[i].numb-1) we must call a rec(i-2) + a[i].numb * a[i].cnt, because we already deleted all (a[i]-1) elements. But if(a[i-1].numb != a[i].numb-1) => there are no elements equal to a[i] — 1 and that means we can simply call rec(i-1) + a[i].numb * a[i].cnt. If we want to skip the current element we just call rec(i-1).

From this => rec(i) = max(rec(i-1), ((a[i].numb == a[i-1].numb + 1) ? rec(i-2) : rec(i-1)) + a[i].numb * a[i].cnt)

And after that you need just to do memoization.

EDIT: The answer will be rec(N). Let the the array be 1-indexed ans rec(0) = 0, rec(1) = a[1].numb*a[1].cnt.

Thank you very much for your explanation :)

h5harsh

can anyone explain how is the merging done in Civilisation problem? How does it guarantee minimum diameter in the resulting tree?..netman

chachachowdhury

Can someone please explain this test case in 455A ?

4 2 3 2 5

how this output is 9?

afrizal

choose any 2 -> delete 3

choose another 2

choose 5 -> delete 4

total 9

how many times i have to choose?

In this case just 3 times (2,2,5). But anyway number of choosing doesn't really matter to optimal choosing. We can get optimal value by more than one way

Mostafa3081

plz what is the algorithm that solve this
i can not solve that one weeks ago

tweety

4 years ago, # |

My solution for Div. 2 B is much simpler. Check if the number is divisible by 4 (check the last two digits), if it is divisible then the answer is 4. Otherwise the answer is 0. I don't know how to prove it but I got Accepted.

bholagabbar

Can someone provide me with a counter-example for the greedy strategy in DIV1-A/DIV2-C? What i did was that i maintained a Map with the sum of every value. Example if 2 occurs 5 times, the map stores 2->10. Now until the map is empty, in each iteration, check for each key in the map: check (sum(current element)- sum(key-1)-sum(key+1)) and store the max for this iteration. Now after this is complete, before the next iteration of the while loop, we add the sum of this max element stored in the map to 'curr score' a variable maintained, and remove key-1 and key+1. This fails for test case 9 which has 100 elements. Please have s look at my solution to get an idea: (http://codeforces.com/contest/455/submission/12642005)

teej

+13

In C, n should actually be max[a[i]]

Arunnsit

can someone explain problem D more gracefully , like more of explanation with simple words? (sqrt decomposition method)

Na2a

Divide an array into blocks. For each block, you have cnt[block_id][x] -> how many x's we have in this block. To do a shift operation, you need to delete last element and insert it before first one. To delete and insert element, you can find where this element is located and delete it (this will take O(sqrt(N)) because size of each block is O(sqrt(N))). But after several queries, some blocks will be too small and some will be too large. That's why you need fully re-construct your sqrt-decomposition after some number of queries.

how can we mantain which element is last in the block the block? i think this will consume o(n) , beacause as we perform a cycle shift , a new element acquires the new position. I was thinking about keeping sqrt(n)queues and then for a shift we always a sqrt operations .. what say?

Look, let us have a two arrays: vector all[numberOfBlocks] and also cnt[numberOfBlocks][maxNumber] to maintain information in blocks. How to do a shift operations? Shift operation is deleting R'th number and inserting it in L'th position.

Now we need insertion and deletion functions.
Take a look at my insertion:

By doing the shift, we change the sizes of blocks. After N queries, some blocks can have no element, while others have O(N) elements. But to make our blocks as close to sqrt(N) as possible, we can totally re-build our decomposition every sqrt(N) queries.

Rebuild is something like this:

After re-building, all blocks will have size of O(sqrt(N)).

bharsi

Div 1 Problem D: I don't understand the need for the array wasVals[][] in the author's solution 7407693. Its only use is to set met[block][value]=0.

Couldn't this be done using the array vals[][]. Will there be a scenario where met[block][value]>0 and vals[block][] does not contain the value?

Edit: I just removed wasVals[][] from author's code and it works 17138498. So looks like it is not needed.

sanngu

BOREDOM PROBLEM EXPLAINATION:-

Let f[i] be the maximum sum he can get from taking only values less than or equal i. Then clearly f[0] = 0 since he can't take any of the aray elements. For other values of i, there are two possible cases. The first case is that he does not take any values from the array that are equal to i (sometimes it is better to not take them so he doesn't have to delete all occurrences of i+1 and i-1). In this case, f[i] = f[i-1]. If he doesn't take any values equal to i, the maximum sum he gets is no different than the maximum sum when he was only allowed to take values up to i-1. The other case is that he does take all occurrences of the value i (it's never optimal to take some but not all occurrences since he has to delete the other elements either way). In this case, he is not allowed to take any occurrences of i-1 since he has to delete them all, but he does get the benefit of adding i * freq[i] to his score (where freq[i] is the number of occurrences of i in the array). The fact that he has to delete all occurrences of i+1 will be taken care of when calculating f[i] so you don't have to worry about that. So in this case f[i] = i * freq[i] + f[i-2]. So when figuring out f[i], you take whichever of these cases results in a higher result. Here is some pseudo-code (assuming you pre-computed freq[i] for all i up to 100,000):

f[0] = 0;
for(int i = 1; i<=100000; i++)
{
f[i] = f[i-1];
if(i > 1) f[i] = Math.max(f[i], f[i-2] + i*freq[i]); // Watch out for overflow here. 
}

NourAlhadi

Sorry but i missed the problem limitation 1<= a[i],b[i] <= n

this was my original comment :D

problem A maybe i miss understood something about the problem statement or solution.. or there is something wrong with the solution..

Sample Input:

1 2

2 3

Solution Output:

Happy Alex

because there exists a pair of a[i],b[i] where a[i]!=b[i] but it's wrong due to problem statement we need to find laptop having less price and higher quality..

Sorry for the long run :D

aadish

You saved me man, i was also getting frustrated on this, guess i also missed this 1<= a[i],b[i] <= n

Glad to hear so :D

....

3 years ago, # |

Can anyone please explain the logic behind tourist's solution: 7390969 for Div 1, D. Serega and Fun problem. It would be of great help. Thanks in advance.

can any one plz help me to understand this plz ?? 455A — Boredom problem f(i) = max(f(i - 1), f(i - 2) + cnt[i]·i), 2 ≤ i ≤ n; f(1) = cnt[1]; f(0) = 0; The answer is f(n).

Manoj2016

DIV 1-E- For a fixed l is clear, it is most optimally that a minimum on the interval [l, y] has been visited by (x - (y - l)) times, and all the other numbers once. this line is not clear to me. will somebody please help me in getting it.

zodiacleo

Hi netman,

For the problem — A Lot of Games
Consider the following two test cases:

Test 1:
2 1
aaaa
ccccc

Author's AC output
First

Comments: The above result makes sense.
Possible scenario:
There are two players, namely, P1 and P2. If P1 start the 1st game (makes him the "First" player), he will always create the word — "ccccc".

Test 2:
2 2
aaaa
ccccc

Comments: This is confusing me!
Possible scenario:
There are two players, namely P1 and P2. If P1 starts the 1st game (which will make him the "First player"), then he will always create the word — "ccccc". So the first game is won by P1. P2 will start the second game (recall — loser of the ith game starts the (i + 1)th game). P2 will also try to create the word — "ccccc". So the second game is won be P2 (who was the "Second" player). Then why does the author's solution say that First player will win the 2nd game?

apoorv92

Wait! You are ignoring one possibility here. What if P1 decides to lose the first game i.e, he chooses the path the results from the string "aaaa". If he does that i.e,he loses, then he will be the one to start the second game. Now for second game, he can choose the path of the string "ccccc", thus, winning the last(k-th) game.

shubho96

2 years ago, # |

Need help for 455A Boredom. The solution gets stuck in the 42nd testcase.

Solution: http://codeforces.com/contest/455/submission/33859161

indweller

19 months ago, # ^ |

If the product of two ints are greater the max value that int can store, the product will overflow, despite the fact that the product variable has been defined as long long. Hence you need to typecast one of the ints to long long. You have to edit your code as (long long) i*cnt[i]. https://www.quora.com/Whats-the-use-of-1ll-in-statement-long-long-l-int-a-*-1ll-*-int-b-in-C-C++

kayak

23 months ago, # |

I am new to competitive programming, can anybody tell why my $\text{[math]}$ submission to Boredom is showing time limit exceeding error in eleventh testcase ?

Also, I don't understand the syntax used in the official C++ solution for boredom, but how you create a array containing the number of occurrence of each elements on O(n) time ?

dalex

23 months ago, # ^ |

Don't use Diagnostics compiler.

mansi_11

20 months ago, # |

In 455D solution, what is meant by rebuilding the structure? Doesn't it gets rebuilded when we update our array(query of type 1) and thus update the blocks.I am very much confused in it.Need help.

acash

13 months ago, # |

will anyone help me?I am new to competitive programming my program is giving wrong output on test case 12 My solution to 455A boredom

N.B.L

13 months ago, # ^ |

acash i just added two small things .. You may check them . 48043440 Don't forget add (return int;) statement at the end of code .

msdcoder7

10 months ago, # |

C. Boredom

Let count[i]=number of times i occured in the input array

dp[i]=maximum points that can be obtained by considering elements upto i

There can be 2 possibilities

case 1: i is selected

If you selecting i, then you have to select all such occurences of i to maximize the points. Also element i-1 cannot be selected because it will be eliminated.

So points scored in this case= i*count[i]+dp[i-2]

case 2: i is not selected

If you are not selecting i, then you have to move over to the next element to score points which is i-1 .

So points scored in this case = dp[i-1]

So thus we get the recurrence relation dp[i]=max(dp[i-1],dp[i-2]+count[i]*i)

cfalas

9 months ago, # |

For Div2E / Div1C, how can one prove the formula for the new diameter? $$$Diameter_{new} = max(Diameter_u, Diameter_v, \left \lceil{\frac{Diameter_u}{2}}\right \rceil + \left \lceil{\frac{Diameter_v}{2}}\right \rceil + 1)$$$

I understand that in the case that the merged part is not connected to the previous diameter, and is not large enough to affect the diameter, it will be the previous diameter, but how do you prove the last part? I know that it is for the case when the two diameters are going to be connected, but cannot fully understand / prove it. How does it ensure that the diameter is minimum? Why does taking half always work?

indian_badass

It seems that if you connect any other two the maximum distance from 1 component to another will be greater than the last value...

ankit_gaga

PROBLEM A(Boredom) can someone help me as my code for problem A wrong on test case #7 my code linkhttps://onlinegdb.com/ryr_SfFnE

Atlas17

6 months ago, # |

Div1.C statement make me confuse @@ "Between any pair of cities there either is a single (unique) PATH, or there is no path at all". I don't think graph is forest until I see editorial ><

abhishek-jha

4 months ago, # |

My solution is failing for 4th test case for problem 1:

	-
Contest:
	-
Type:
	-

netman's blog