BIT does not support insert operator, but Skip list does. I realized that we can transform a Skip list into a BIT.
Example source code for impatient people:
http://paste.ubuntu.com/8119698/
My data-structure contains some operators:
- Insert x v: insert an element valued v into position x:
For instance: {10,20,30} -> insert 40 3 -> {10,20,40,30}
- Range-sum x y: return sum of elements in ranges x..y
For instance: {10,20,30} -> range-sum 2 3 -> 50
Average complexity of each operator is O(log (max n))
1. Property
a. Parent — child relationship
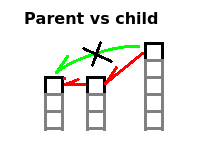
A is parent of B if A is the first node on the right of B and A is not shorter than B (A is higher or at least equal B height).
b. Sum and Count
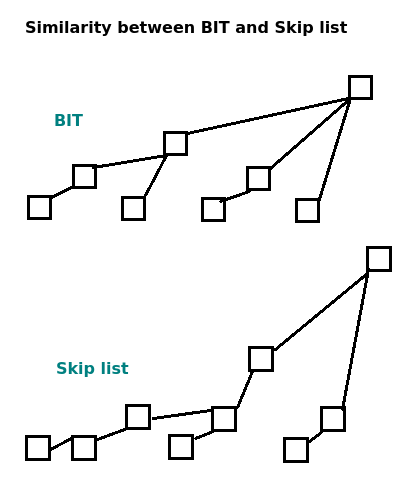
In each node, we maintain a value Sum and Count.
Assume u has children u1, u2, ...
Sum[u] = Value[u] + Value[u1] + Value[u2] + ...
Count[u] = 1 + Count[u1] + Count[u2] + ...
2. Operators
a. Accessing an element x-th
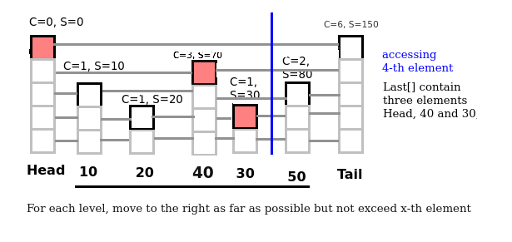
- For each level (from 19 to 0), we move as far as possible but still not over x-th element (We use value Count in each node to ensure that we not go over x-th element). Additionally, we must keep array Last[] contain id of last element not exceed x-th element (to use this for later operators).
b. Insert an element into position x
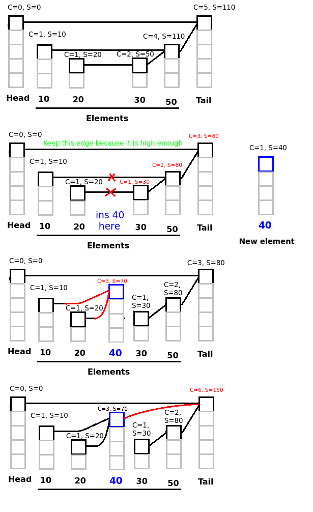
- Access (x-1)-th element, Last[] let us know edges between (x-1)-th and x-th element.
- Disconnect short edges (edges which height <= new element's height), maintain Sum and Count of other elements.
- Insert new element, connect some necessary elements in Last[] with the new element, maintain Sum and Count of relevant elements.
- Connect new element with its parent, maintain Sum and Count of relevant elements.
c. Get sum of a range
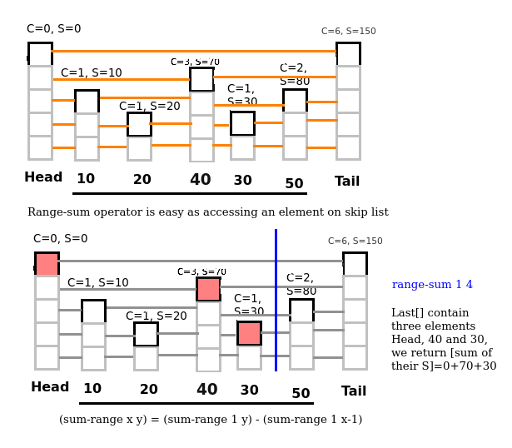
Realize (Range-sum x y) = (Range-sum 1 y) — (Range-sum 1 x-1), therefore we only need to process (range-sum 1 x).
- Access x-th element
- Get sum of all of elements in Last[], if an element twice or more, we only plus once.
For example, Last[]={0,0,0,2,3,3,3} -> Answer = Sum[0] + Sum[2] + Sum[3]
3. Example source code
http://paste.ubuntu.com/8119698/
- I tested it and it worked correctly.
- It run fast, complexity of each query is about 2.5 * log (max n)











Nice! Fenwick approach on skip-list looks really easy and intuitive.
Has anyone ever compared skip-lists and cartesian trees (as the most simple self-balancing BST) performance?
Thanks. I have tried some benchmark on my computer. Intel Pentium 2.2GHz.
Looks really inefficient. It's much better to generate random 20-bit integer
xand makeLevel[u] += __builtin_ctz(x)(number of trailing zeros in binary representation of x). This should decrease runtime twice.EDIT: Sorry, I have a mistake. Your improvement does not make running time smaller. I used __builtin_ctz(x) but it is wrong, must be __builtin_ctz(x)+1. Running time is still not changed.
really awesome tutorial (especially the pictures)! :)
thanks
What did you use to draw pictures?
Kolourpaint on ubuntu