466A - Cheap Travel
Solution of this problem is based on two claims:
— If m·a ≤ b then there is no point to buy a ride ticket.
— Sometimes it is better to buy summary more ride tickets for amount of rides than we need.
If we receive profits bying ride tickets then number of such ones will be 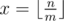 . For the remain n - m·x rides we must choose the best variant: to buy separate ticket for each ride, or to buy ride ticket and use it not fully.
. For the remain n - m·x rides we must choose the best variant: to buy separate ticket for each ride, or to buy ride ticket and use it not fully.
Complexity: O(1)
Solution: 7784793
466B - Wonder Room
Let’s assume that a ≤ b.
First of all, let’s consider the situation when we can already accommodate all the students. If 6·n ≤ a·b then answer is a·b a b.
Otherwise, we have to increase one of the walls(maybe, both). Let’s do it in the following way: iterate the size of the smallest wall newa (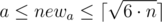 ), after that we can calculate the size of another wall as
), after that we can calculate the size of another wall as 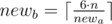 .
.
For all this newa and newb if b ≤ newb we choose such a pair that has the smallest area of a room.
Obviously to undestrand, that there is no point to consider 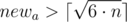 because we can decrease it and receive room of smaller area when we know that
because we can decrease it and receive room of smaller area when we know that 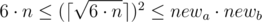 .
.
Complexity: 
Solution: 7784788
466C - Number of Ways
First of all, notice that if sum of all elements is equal S then sum of each of three parts is equal 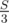 .
.
Therefore, if S is not divided by 3 — then answer is 0.
Otherwise, let’s iterate the end of first part i (1 ≤ i ≤ n - 2) and if sum of 1..i elements is equal 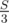 then it means that we have to add to the answer the amount of such j (i + 1 < j) that the sum of elements from j-th to n-tn also equals
then it means that we have to add to the answer the amount of such j (i + 1 < j) that the sum of elements from j-th to n-tn also equals 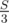 .
.
Let’s create an array cnt[], where cnt[i] equals 1, if the sum of elements from i-th to n-th equals 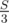 and 0 — otherwise. Now, to calculate the answer we have to find the sum
and 0 — otherwise. Now, to calculate the answer we have to find the sum cnt[j] + cnt[j+1] + ... + cnt[n] faster then O(n). There are a lot of required ways to do this, but the easiest one is to create a new additional array sums[] where in j-th element will be cnt[j] + cnt[j+1] + ... + cnt[n]. It is easy to calculate in such way: sums[n] = cnt[n], sums[i] = sums[i+1] + cnt[i] (i < n).
Thus, we receive very simple solution: for each prefix of initial array 1..i with the sum that equals 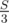 we need to add to the answer
we need to add to the answer sums[i+2].
Complexity: O(n)
Solution: 7784781
466D - Increase Sequence
Lets use dynamic programming to solve this problem. dp[i][opened] — the number of ways to cover prefix of array 1..i by segments and make it equal to h and remain after i-th element opened segments that are not closed.
Consider all possible variants opening/closing segments in each position:
- ] closing one segment
- [ opening one new segment
- [] adding one segment with length 1
- ][ closing one opened segment and opening a new one
- - do nothing
Lets understand how to build dynamic. It is obviously to understand that a[i] + opened can be equal h or h - 1. Otherwise, number of such ways equals 0.
Consider this two cases separately:
1) a[i] + opened = h
It means that number of opened segments after i-th as max as possible and we can’t open one more segment in this place. So there are two variants:
- [ Opening a new segment. If only opened > 0. dp[i][opened] += dp[i-1][opened + 1]
- - Do nothing. dp[i][opened] += dp[i-1][opened]
Other variants are impossible because of summary value of a[i] will be greater than h(when segment is finishing in current position — it increase value, but do not influence on opened, by the dynamic definition.
2) a[i] + opened + 1 = h
Here we consider ways where i-th element has been increased by opened + 1 segments, but after i-th remain only opened not closed segments. Therefore, there are next variants:
- ] — closing one of the opened segments(we can do it opened + 1 ways). dp[i][opened] += dp[i-1][opened + 1] * (opened + 1)
- [] — creating 1-length segment. dp[i][opened] += dp[i-1][opened]
- ][ — If only opened > 0. Amount of ways to choose segment which we will close equals opened. dp[i][opened] += dp[i-1][opened] * opened
Start values — dp[1][0] = (a[1] == h || a[1] + 1 == h?1:0); dp[1][1] = (a[1] + 1 == h?1:0)
Answer — dp[n][0].
Complexity: O(n)
Solution: 7784697
466E - Information Graph
Let’s introduce all structure of the company as a graph(if у is the head of х then we add edge y -> x). It is obviously to understand that after each operation our graph will be the set of trees. Actually, the third query — to check is our vertex belong to the subtree of the vertex which has received data package. Graph that we will receive after doing all operations we call final. Also, we will say that two vertexes belong to the same connectivity component if they belong to the same component in graph that we can have from final by changing directed edge to undirected.
Consider the following statement: vertex у is the parent of vertex х in current graph(after doing first i queries) if у and х belongs to the same conectitive component and in final graph у is the parent of х.
We will solve this problem offline. After each query of adding data package we will immediately answer all the questions about this package. Besides that, use disjoint set union to define is this vertex belong to the same component or not. To answer the question we need to check that y is the parent of x in final graph and that x and y is currently belong to the same connectivity component. Final graph we will build before doing this algorithm because we know all queries. Check that y is the parent of x in final tree we can simply in O(1) by arrays of entry-time and output-time which we can calculate use dfs(v —parent u <=> (in[v] ≤ in[u] and out[u] ≤ out[v]).
Complexity: O(n * u(n)), where u — inverse Ackerman function.
Solution: 7784662











I solved C a bit another way with DP: http://codeforces.com/contest/466/submission/7770043 First consider the case when Σ a = 0, where a is input. Then count the number dp of all indexes i from 0 to n - 2, for which Σ0ia = 0. The answer is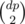 .
.
Now consider the case when s = Σ a ≠ 0. Take two lists dp0 and dp1. dp0 will contain all indexes i, for which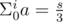 , and dp1 will contain all indexes j, which satisfy
, and dp1 will contain all indexes j, which satisfy 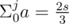 . Now remains a bit tricky part, which can get TLE, if not correctly implemented: count all ordered pairs from dp0 and dp1. This can be done in linear time by looping through dp1 and saving current dp0 index:
. Now remains a bit tricky part, which can get TLE, if not correctly implemented: count all ordered pairs from dp0 and dp1. This can be done in linear time by looping through dp1 and saving current dp0 index:
The loop is O(n2); consider if the input is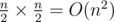 pairs.
pairs.
1 0 0 0 ... 0 1 0 0 0 ... 0 1, so that dp0 holds every index in the first half of the array, and dp1 holds every index in the second half of the array. Now you're looping throughThe above method seems O(n) , since each index in dp0 is traversed only once.
I solved C the pretty much same way as yours. Although I save the sum from a[0] to a[i] (with i looped from 0 to n) to a variable and compare them to s/3 and 2s/3, if one of the conditions hold we add one to counter f (similar to your dp0) or add f to counter ct (as there would be f way to split 0->i to 2 equal parts), respectively. That way we have an O(n) solution. My solution: 7766244
Thanks
Hope so that D & E really comes soon !
I didn't quite understand Problem B's solution in the end. Why no need to consider newa > ceiling(sqrt(6n)) ? can someone give more details?
The editorial says that newa is the smaller side; if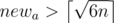 , you can prove that this makes
, you can prove that this makes 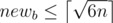 and hence newa is not the smaller side.
and hence newa is not the smaller side.
But how do we know that new a is smaller side? Can't it be new b?
I don't quite understand the editorial for C. However, here's my solution. This is probably DP, although the fact that it might be DP doesn't come to my mind.
The first part is the same as the editorial's; find the sum s and if it's not divisible by 3, return 0.
On the second part, we keep three variables: t for the sum of all elements up to this point, ct to count the number of prefixes whose sum is , and res to count the actual number of pairs.
, and res to count the actual number of pairs.
We loop over each element except the last one; suppose the current element is p. We add p to t. If this causes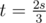 , we add the value of ct to res. If this causes
, we add the value of ct to res. If this causes  , we increment the value of ct. We do this in that order; switching won't work (try input
, we increment the value of ct. We do this in that order; switching won't work (try input
0 0 0; expected answer is1but switching the order of the above gives3). This gives O(n) time with O(1) memory besides storing the array, better than the proposed O(n). Now why does that work?First, observe that ct holds the number of ways we can cut the array into two such that the left part sums to and the right part sums to
and the right part sums to 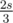 , where the cut is done before p.
, where the cut is done before p.
Whenever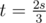 , it means the last part sums to
, it means the last part sums to  . Now, ct holds the number of ways we can cut the array so that the left part sums to
. Now, ct holds the number of ways we can cut the array so that the left part sums to  before p. So we now have ct possible divisions: the first cut is any cut that ct has counted, giving a left part of
before p. So we now have ct possible divisions: the first cut is any cut that ct has counted, giving a left part of  , and the second cut is right after p, giving a right part of
, and the second cut is right after p, giving a right part of  (since the sum of the left and middle parts is
(since the sum of the left and middle parts is 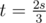 ). And the middle part is of course
). And the middle part is of course  by elimination. Thus we increase res by ct.
by elimination. Thus we increase res by ct.
Now we update ct. If , dividing right after p gives a left part summing to
, dividing right after p gives a left part summing to  , so this should now be counted by ct for future iterations. Note that we don't do this before the above so that our program won't mistakenly divide the array in the same place; if we update ct first, cutting right after p is now counted in ct, and if we also increase t, we will count dividing right after p among the possible ways, and thus both cuts happen right after p; this doesn't work for obvious reasons.
, so this should now be counted by ct for future iterations. Note that we don't do this before the above so that our program won't mistakenly divide the array in the same place; if we update ct first, cutting right after p is now counted in ct, and if we also increase t, we will count dividing right after p among the possible ways, and thus both cuts happen right after p; this doesn't work for obvious reasons.
Thus, after every iteration, ct holds the number of ways to split the array somewhere before the next element into two such that the first part sums to , and res holds the current total number of ways sought, where the splits are done before the next element. Since the loop finishes at the penultimate element, res now holds the number of ways to split the array as stated where the splits are done before the last element, which is the number we seek. (If we advance one more, it's possible that res counts where the second cut is at the end of the array, giving an empty third part, not accepted.)
, and res holds the current total number of ways sought, where the splits are done before the next element. Since the loop finishes at the penultimate element, res now holds the number of ways to split the array as stated where the splits are done before the last element, which is the number we seek. (If we advance one more, it's possible that res counts where the second cut is at the end of the array, giving an empty third part, not accepted.)
I hope the above is clear. The algorithm itself fits in three paragraphs (paragraphs 2-4 above); the proof is what makes everything bloaty.
Another way to solve C is to take the indexes strictly smaller than n where the sum from the beginning is exactly sum/3 and the indexes strictly smaller than n where the sum from the beginning is exactly 2*sum/3. Lets call these sets idx1 and idx2. Obviously they will be sorted because we iterate from 1 to n-1. For every index from idx1 we count the indexes from idx2 which are strictly greater than our current. This could easily be done in O(logn) using binary search. Total complexity: O(nlogn). My solution.
We can use two pointers method for that instead. If we have idx1 and idx2 as you described, begin with two pointers a = 0, b = 0. We compare idx1[a] and idx2[b]; if idx1[a] < idx2[b], we increment a, otherwise we increment b. Whenever we increment b, add a into the result. This works in O(n), and is essentially my solution just above (although mine works online, without storing idx1 and idx2 in memory).
Indeed what I done. http://codeforces.com/contest/466/submission/18943449
Exactly what i did to solve this problem. The complexity of this approach is $$$O(n\ log (n))$$$ and that is enough to pass tests.
how to solve E??
I am unable to understand the solution for problem D and please clear me the meaning of dp[i][opened].
Maybe it is easier to understand.
Thanks, that did the work. Maybe translation from Russian to English is not perfect and some meaning is lost in between.
In D,while a[i] + opened = h,why can we open a segment?Then,a[i]will bigger than h.Is it a mistake?
Maybe I am wrong
dp[i][opened]means you solved for positioni(meaning converted a[i] to h) and after that from(i+1)thposition you are left withopenednumber of open segments.Now you have 2 valid cases
i-1you haveopenednumber of segments.Since a[i] is already increased by opened number we do nothing here-dp[i][opened] += dp[i-1][opened]i-1you haveopened-1number of segments. Since there is a need of increasing a[i] by one we are bound to open a segment here.[dp[i][opened] += dp[i-1][opened - 1]//Typo in tutorial, see his solutionWe don't close here in any case as we will have
opened -1open segments after it.So]and[]cases are ruled out. Also][will makea[i] = h+1so its also ruled out.I have known it,thank you anyway
I am unable to understand the solution of problem E ,would anyone like to explain the problem E ??
if u dfs the final graph and traverse it preorder and write their discovery times, then u can understand whether a node is parent of another. and with dsu you can keep track of the nodes which are in the same group. using both of these you can understand whether someone signs a document or not
Err..I've made a mistake.... Just ignore me, please..
i got my problem B code accepted by O(n).
How did you do it?
There is typo in D (1) first case: it should be dp[i][opened] += dp[i-1][opened — 1]
I wasted a lot of time bcoz of this typo in the editorial.Thank you.
In Problem D . We can close more than one segments as in the case a[i]+opened+2=h we can close 2 segments here, but in the Editorial it's considering the case of closing only one segment. Can anyone tell how it will produce right answer. Thanku...
Don't know if you are still looking for answer, but in case you do: there is a restriction in the problem that you can't close more than one segment on each position. It's stated in the last sentence of the first paragraph.
sorry, i can not understand the solution of e, can anyone clear it, thank very much
Can anyone please explain the solution of 466D — Increase Sequence. I am unabel to understand the solution given in editorial.
Can anyone explain me solution D..??
Antoniuk nice fall :) For two contest you will beat dreamoon_love_AA.
Problem-C 466C - Number of Ways is exactly the same problem as 21C - Stripe 2 ...Nothing to say !!
i am having problem understanding the solution of C.
let’s iterate the end of first part i (1 ≤ i ≤ n - 2) and if sum of 1..i elements is equal S/3 then it means that we have to add to the answer the amount of such j (i + 1 < j) that the sum of elements from j-th to n-tn also equals S/3 .
why not such j(i<j)?
If j = i + 1, there would be no 2'nd part.
In problem C why do we do cnt[i]+=cnt[i+1] and at the end ans+=cnt[i+2] ?
Because if on some prefix sum is [S/3] we should add all the methods of getting exactly this sum on our suffix. Why [i + 2]? Because we should have 3 parts with exactly the same sum.
I had serious difficulty in understanding the editorial of problem D. Took me a good amount of time to reach the solution. This comment helped a lot.
Here's the approach: Firstly, if there exists an element in the array >= h, there is no way, so the answer is 0.
Now, let dp[i][j] denote the no. of ways to make the first i points be equal to h s.t. there still remain j open segments after the point j. Now, there are 5 possibilities at a particular element:
Don't open or close any segment here: In this case, we require j + a[i] == h and the no. of open segments after (i-1)st element must also be j. So, here we consider the no. of ways to make first (i-1) elements to be equal to h s.t. there exist j open segments after it. So, we add dp[i-1][j] to dp[i][j].
Open a segment here and don't close any: We require a[i] + j == h and no. of open segments after (i-1) must be (j-1). So, we add dp[i-1][j-1] to dp[i][j].
Close a segment here and don't open any: We require a[i] + (j + 1) == h since total contribution to ith element is by (j+1) segments (j which still remain open and 1 which is closed) and no. of open segments after (i-1) must be (j+1). Note here that there are also (j+1) ways to choose the segment we close at i. So, we add (j+1) * dp[i-1][j+1] to dp[i][j+1].
Open and close a segment here (length 1 segment): We require a[i] + (j + 1) == h and no. of open segments after (i-1) elements must be j. So, we add dp[i-1][j] to dp[i][j].
Close a previously opened segment and open a new segment: We require a[i] + (j + 1) == h and no. of open segments after (i-1) elements be j. Also, there are j ways to choose the segment to close. So, we add j * dp[i-1][j] to dp[i][j].
The answer to the problem is simply dp[n][0].
Here's my submission: 45472102
The last line of the explanation of problem E is a little ambiguous. Here's the actual interpretation:
...which we can calculate using dfs(). If v is an ancestor of u, then it must hold that in[v] ≤ in[u] and out[u] ≤ out[u].
One more point: the above condition holds iff we ensure that in the final set of trees, every dfs performed on a tree starts at the root node. For this in the main loop of dfs(), for all the vertices processed in sequence, we can check if that vertex has not been visited and it is the root node of a tree (its indegree is 0), we can perform dfs starting from that vertex by calling a function that performs the dfs (say dfs_()). Here's my code: 46903908
Please explain Problem C in simple words. I am facing lot of difficulties in understanding the approach. I tried to dry run the code for various test cases but couldn't figure out the approach.
just make a suffix array where each value represent ......the number of times the sum/3 appear . then simply iterate every element of array and if at some index the sum =sum/3 ..then leave the one index and check i.e i+2 th index
code
to cal suffix array
...
...
why i+2 ? because you have to divide the array in 3 part so second part we have to leaave atleast 1 element...
~~~~~
Do you know what actually is a suffix array?
suffix array is for 3rd partition.
it stores, the number of times the total sum equals to sum/3.
3 3 -3 3 3
sum =9
sum=sum/3=3;
[see "to cal suffix array code" in my previous comment] array 3 3 -3 3 3(arr)
suffix 0 0 1 0 1
suffix sum of ::
0 0 1 0 1
2 2 2 1 1 (suff)
so, we are at 0 th index in arr and sum upto this index is sum/3 i.e 3
then we check for i+2 th index of suffix we see that value is 2 i.e we have
two indices(idx==>2 and 4 in arr ..so we have two choice to partition third part) where sum is equal to sum/3 i.e 3 as we see in original aray
arr 3 3 -3 3 3
first choice idx 2 -->3 | 3 |-3 3 3
second choice idx 4-->3 | 3 -3 3 |3
now moving forward in first part ...we see that at index 2 again in arr sum is equal to sum/3 i.e 3
then in suffix i+2 i.e 4 index in suff ,value is 1
this means we have only one index having sum=sum/3
so in arr we have one choice only ::3 3 -3| 3 | 3
so ans is total choices 2+ 1=3
Those are usually called suffix sums.
A suffix array is a much more complex data structure.