Hi! :)
What is the best upper bound for number of divisors of some natural number n?
I can't find any bound better than 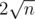 :(
:(
→ Pay attention
→ Top rated
| # | User | Rating |
|---|---|---|
| 1 | tourist | 3880 |
| 2 | jiangly | 3669 |
| 3 | ecnerwala | 3654 |
| 4 | Benq | 3627 |
| 5 | orzdevinwang | 3612 |
| 6 | Geothermal | 3569 |
| 6 | cnnfls_csy | 3569 |
| 8 | jqdai0815 | 3532 |
| 9 | Radewoosh | 3522 |
| 10 | gyh20 | 3447 |
→ Top contributors
| # | User | Contrib. |
|---|---|---|
| 1 | awoo | 161 |
| 1 | maomao90 | 161 |
| 3 | adamant | 156 |
| 4 | maroonrk | 153 |
| 5 | -is-this-fft- | 148 |
| 5 | atcoder_official | 148 |
| 5 | SecondThread | 148 |
| 8 | Petr | 147 |
| 9 | nor | 144 |
| 10 | TheScrasse | 142 |
→ Find user
→ Recent actions
↑
↓
Codeforces (c) Copyright 2010-2024 Mike Mirzayanov
The only programming contests Web 2.0 platform
Server time: Jul/27/2024 03:38:25 (g1).
Desktop version, switch to mobile version.
Supported by
User lists


| Name |
|---|











n^1/3 are often used bound
As far as I remember, it's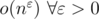 . But you can use
. But you can use 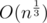 in practice.
in practice.
UPD: link and discussion on Codeforces (Russian)
T0RRES and yeputons, thank you both!
Regarding the number of divisors, a useful thing for programming contests is to search OEIS for "1344 maximal divisors", or just memorize the sequence numbers for the maximal number of divisors and also the smallest and largest n-digit integers that have the appropriate number of divisors. The two latter sequences are sometimes useful in test cases.
The number is 1344 for integers up to 109 and 103 680 for integers up to 1018.
Well, an exact answer is always better than an approximation.
http://ideone.com/JNRMsQ
This calculates the maximum number of divisors of any positive integer less than n, given n as input. n <= 10^18.
Hope this helps.
.
Maximum number of divisors of any positive integer less than n. 72 indeed has 12 divisors
.
This calculates the maximum number of divisors of any positive integer less than n, given n as input. n <= 10^18.
What about this do you not understand?
.
Uhm... Basically everything. The code wasn't intended to answer your query. Before asking, why not google? The first answer I got was this
And here is a list of first few hundreds of highly composite numbers:)
Gassa, hashlife, I_love_Tanya_Romanova. Thank you guys! :)
I got exactly what i was looking for.
if n=(p1^a1)(p2^a2)..(pk^ak)where pi are different primes then n have exactly (a1+1)(a2+1)(ak+1)different divisors but p1>=2,p2>3 etc, so a1<=log2(n), a2<=log3(n/p1^a1)=log3(n)-a1*log3(2), a3<=log5(n)-a1*log5(2)-a2*log5(3),.. and O(n^eps)as result
I understood why $$$2\sqrt{n}$$$ is an upper bound. But can somebody explain the reasoning behind the upper bound being $$$\mathcal{O}(n^{\frac{1}{3}})$$$?
It's not really true in a way you would expect. That statement with $$$n^\frac{1}{3}$$$ should be taken with a grain of salt. It is a mere heuristic that tells you what is more or less the number you could expect if we are talking about numbers that appear within competitive programming, e.g. $$$\le 10^{18}$$$. There is no connection between $$$n^\frac{1}{3}$$$ and maxium number of divisors other than they are of similar order of magnitude for numbers of that size.