Can somebody describe their solution to http://codeforces.com/gym/100519/problem/I ? Somehow I can't shake the feeling that it's enough to always multiply with 2, but I cannot substantiate my intuition to turn this into an algorithm.
→ Pay attention
→ Streams
→ Top rated
| # | User | Rating |
|---|---|---|
| 1 | tourist | 3880 |
| 2 | jiangly | 3669 |
| 3 | ecnerwala | 3654 |
| 4 | Benq | 3627 |
| 5 | orzdevinwang | 3612 |
| 6 | Geothermal | 3569 |
| 6 | cnnfls_csy | 3569 |
| 8 | jqdai0815 | 3532 |
| 9 | Radewoosh | 3522 |
| 10 | gyh20 | 3447 |
→ Top contributors
| # | User | Contrib. |
|---|---|---|
| 1 | awoo | 161 |
| 2 | maomao90 | 160 |
| 3 | adamant | 156 |
| 4 | maroonrk | 153 |
| 5 | atcoder_official | 148 |
| 5 | -is-this-fft- | 148 |
| 5 | SecondThread | 148 |
| 8 | Petr | 147 |
| 9 | nor | 144 |
| 10 | TheScrasse | 142 |
→ Find user
→ Recent actions
↑
↓
Codeforces (c) Copyright 2010-2024 Mike Mirzayanov
The only programming contests Web 2.0 platform
Server time: Jul/27/2024 07:35:07 (h1).
Desktop version, switch to mobile version.
Supported by
User lists


| Name |
|---|











spoiler
The first one is more along the lines of what I was thinking :) The second idea is magical.
It became one of my favourite problems few days ago :)! Indeed, we will use just multiplying by 2. Consider fraction . If we have a fraction f, we multiply it by 2 and then receive information ">" we know that
. If we have a fraction f, we multiply it by 2 and then receive information ">" we know that 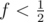 and if we receive "<", we know that
and if we receive "<", we know that 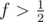 . Inductively if we receive informations "<<>><><" and we change each "<" to "1" and ">" to "0" (unless p! = 2 we can't receive "=") we got a prefix of binary representation of f (following "0."), so "<<>><><" changes to "0011010" and we know that
. Inductively if we receive informations "<<>><><" and we change each "<" to "1" and ">" to "0" (unless p! = 2 we can't receive "=") we got a prefix of binary representation of f (following "0."), so "<<>><><" changes to "0011010" and we know that 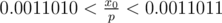 . Using 40 questions we can get approximation of
. Using 40 questions we can get approximation of 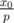 with error at most 2 - 40, but if
with error at most 2 - 40, but if 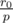 and
and 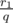 are potential starting fractions we know that
are potential starting fractions we know that  , so this precision is sufficient to uniquely determine starting fraction :)!
, so this precision is sufficient to uniquely determine starting fraction :)!
Oh wow, that's a really nice solution! Thanks for sharing.
Amazing!
Oh my god
A wise man.^_^