Last SRM's div1-250-task raised two questions:
- how to calculate square root of a perfect square?
- how to do a perfect square test?
The following two methods solve these problems correctly in Java:
long rootOfPerfectSquare(long xx) { return (long) Math.sqrt(xx); }boolean isPerfectSquare(long xx) { long x = (long) Math.sqrt(xx); return x * x == xx; }
What makes correctness non-obvious is implicit conversion of Math.sqrt() argument from long to double, where precision can be lost.
Correctness can be verified using the following code:
for (long x = 0; x <= Math.sqrt(Long.MAX_VALUE); x++)
if (x != (long) Math.sqrt(x * x)) System.out.println(x);
Is there any explanation of why it works?
Does this method work in other languages, e.g. C++?
Can you prove or disprove the following statement: for any long x >= 0: 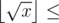 (long) Math.sqrt(x)
(long) Math.sqrt(x) 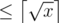 ?
?











I've tested it in C++.
It works well. But, this is only true when you are calculating square root of a perfect square. In other word, you can't test if number x is perfect square by
sqrt(x)*sqrt(x)==x. It's because, in IEEE754doubleis defined 52-bit accuracy and there is no way to distinguish x2 + 1 from x2 if it's larger than 252. BothMath.sqrt()in Java andsqrt()in C++ receivedoubleas argument.I don't think this is necessary. Just consider the following cases.
Case 1: x is a perfect square If x is a perfect square, then there's a y such that y*y = x. As loujunjie has pointed out, if x is a perfect square, then (long) sqrt(x) will return the exact square root of x, which in this case is y. So in this case, it's correct to say that if x is a perfect square, then (long) sqrt(x) will give us it's exact square root.
Case 2: x is not a perfect square If x is not a perfect square, then there is no such y such that y*y = x. So it doesn't matter what (long) sqrt(x) gives us, (long)sqrt(x) * (long)sqrt(x) will never be equal to x.
That is why it is sufficient to do just the following:
I don't know if it's necessary or not, and I don't want to know. I just write code that is 100% working and doesn't care about implementation of floating point types.
It's hardcoded in the IEEE 754 standard, the result of sqrt(x) will be the closest representable number to the square root of x. If the square root is representable then sqrt(x) will be exact.
In Java if we pass 64-bit long value x to Math.sqrt(x), then x will be implicitly converted to 64-bit double and certainly some precision can be lost. In spite of this, (long) Math.sqrt(x) gives exact answer for perfect squares. How can it be explained?
I'm not sure how C++ converts long long argument passed to sqrt(): is it converted to double or long double and can there be any loss of precision?
In C,
sqrtis definedIn C++98
sqrtis definedSo it may work. But
long doubleis machine-dependent. We should avoid it.However, in C++11, one overloaded
sqrtis definedI think it will work well for
long longargument. I'll do some tests.UPD1: Test of C
result is 2000000000. It's not 1999999999, which is what we supposed.
UPD2: Test of C++98 and C++11 also give same result, that is 2000000000.
The C++ reference said:
"Additional overloads are provided in this header () for the integral types: These overloads effectively cast x to a double before calculations (defined for T being any integral type)."