Edit (Jan 22, 2:45 AM UTC): Added Div1E and the editorial is now complete. I am sorry for the delay.
Edit (Jan 21, 9:45 AM UTC): Added the explanation for Div1C/2E, and the problem setters' codes. Div1E will need several more hours. Thank you again for your patience.
First, here are some statistics on this round:
| Division | Registrants | Participants | A Accepted | B Accepted | C Accepted | D Accepted | E Accepted |
| 1 | 1364 | 572 (*) | 294 | 199 | 8 | 113 | 1 |
| (Estimated number of AC by me) | 800 (wrong) | 500 (wrong) | 70 (FAIL) | 90 (ok) | 5 (wrong) | ||
| 2 | 4016 | 2028 | 1355 | 945 | 41 | 5 | 0 |
We are sorry for terribly underestimating the difficulty of the problems (except Div1D), especially Div1A/2C and Div1C/2E.
Div.2 A: 505A - Mr. Kitayuta's Gift
[Problem] Given a string, turn it into a palindrome by inserting one letter or state that it is impossible.
(Problem by evima)
Since the string is short (at most 10 characters), you can simply try every possible way of inserting a letter ("where" and "what" to insert), and check if the resulting string is a palindrome.
The writer's code (C++): 9501249Note: For some strange reason, we (contest managers) cannot submit solutions so that everyone can see them. PraveenDhinwa told us how to do so. Thank you!
Div.2 B: 505B - Mr. Kitayuta's Colorful Graph
[Problem] Given an undirected graph whose edges are painted in colors, process the queries of the following form:
- Given two vertices ui and vi, find the number of the colors that satisfies the following condition: the edges of that color connect ui and vi (possibly indirectly).
(Problem by hogloid)
Since neither the graph nor the number of queries is too large, for each query you can simply count the number of the "good" colors (the colors that satisfies the condition) by checking if each color is "good". To do that, you can perform Depth First Search (or Breadth First Search) and verify whether you can reach vi from ui traversing only the edges of that color. If you prefer using Union-Find, it will also do the job.
The writer's code (DFS, C++)
The writer's code (Union-Find, C++)
Div.2 C / Div.1 A: 505C - Mr. Kitayuta, the Treasure Hunter
[Problem] Since it is hard to summarize this problem, please refer to the official statement.
(Problem by yosupo)
Below is the explanation from yosupo, translated by me.
[From here]
Let m be the number of the islands (that is, 30001). First, let us describe a solution with time and memory complexity of O(m2).
We will apply Dynamic Programming. let dp[i][j] be the number of the gems that Mr. Kitayuta can collect after he jumps to island i, when the length of his previous jump is j (let us assume that he have not collect the gems on island i). Then, you can calculate the values of the table dp by the following:
- dp[i][j] = 0, if i ≥ m
(actually these islands do not exist, but we can suppose that they exist and when Mr. Kitayuta jumps to these islands, he stops jumping) - dp[i][j] = (the number of the gems on island i) + max(dp[i + j][j], dp[i + j + 1][j + 1]), if i < m, j = 1
(he cannot perform a jump of length 0) - dp[i][j] = (the number of the gems on island i) + max(dp[i + j - 1][j - 1], dp[i + j][j], dp[i + j + 1][j + 1]), if i < m, j ≥ 2
This solution is unfeasible in terms of both time and memory. However, the following observation makes it an Accepted solution: there are only 491 values of j that we have to consider, which are d - 245, d - 244, d - 243, ..., d + 244 and d + 245.
Why? First, let us find the upper bound of j. Suppose Mr. Kitayuta always performs the "l + 1" jump (l: the length of the previous jump). Then, he will reach the end of the islands before he performs a jump of length d + 246, because
d + (d + 1) + (d + 2) + ... + (d + 245) ≥ 1 + 2 + ... + 245 = 245·(245 + 1) / 2 = 30135 > 30000. Thus, he will never be able to perform a jump of length d + 246 or longer.
Next, let us consider the lower bound of j in a similar way. If d ≤ 246, then obviously he will not be able to perform a jump of length d - 246 or shorter, because the length of a jump must be positive. Suppose Mr. Kitayuta always performs the "l - 1" jump, where d ≥ 247. Then, again he will reach the end of the islands before he performs a jump of length d - 246, because
d + (d - 1) + (d - 2) + ... + (d - 245) ≥ 245 + 244 + ... + 1 = 245·(245 + 1) / 2 = 30135 > 30000. Thus, he will never be able to perform a jump of length d - 246 or shorter.
Therefore, we have obtained a working solution: similar to the O(m2) one, but we will only consider the value of j between d - 245 and d + 245. The time and memory complexity of this solution will be O(m1.5), since the value "245" is slightly larger than 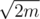 .
.
This solution can be implemented by, for example, using a "normal" two dimensional array with a offset like this: dp[i][j - offset]. The time limit is set tight in order to fail most of naive solutions with search using std::map or something, so using hash maps (unordered_map) will be risky although the complexity will be the same as the described solution.
[End]
The writer's code (memoized recursion, C++)
Div.2 D / Div.1 B: 505D - Mr. Kitayuta's Technology
[Problem] Given an integer n and m pairs of integers (ai, bi) (1 ≤ ai, bi ≤ n), find the minimum number of edges in a directed graph that satisfies the following condition:
- For each i, there exists a path from vertex ai to vertex bi.
(Problem from evima)
Let G1 be the directed graph built from the input, and G2 be a directed graph that satisfies the given conditions. What we seek is the minimum number of edges in G2. Also, we say that two vertices u and v in a directed graph are "weakly connected" if we can reach v from u by traversing edges, not considering their directions.
If a pair (u, v) is present in the input, then vertices u and v must be weakly connected in G2. Therefore, for each weakly connected component (abbreviated to wcc) in G1, the vertices in that component must also be in the same wcc in G2. We can "merge" multiple wccs in G1 and create a larger wcc in G2, but for now, let us find the minimum number of edges required in G2 for each wcc in G1 when we do not "merge" them. There are two cases to consider:
- If a wcc in G1 does not have cycles, then we can perform topological sort on that wcc, and we can make a "chain" (see the image below) using the topological order to satisfy the conditions. We need (the number of the vertices in the wcc) - 1 edges, which is the minimum required number since any connected graph with V vertices has at least V - 1 edges.
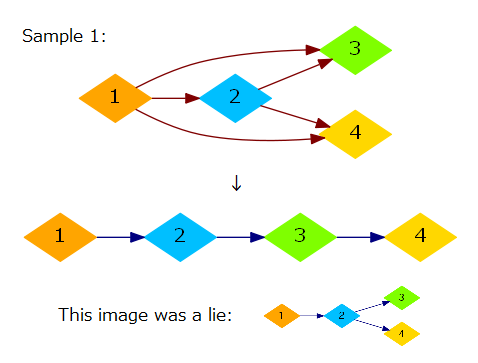
- If a wcc in G1 has cycles, then topological sort cannot be applied. We need at least (the number of the vertices in the wcc) edges this time, since any connected graph with V vertices and V - 1 edges is a tree, which does not contain cycles. Actually, this number (the number of the vertices in the wcc) is always achievable by connecting the vertices into a "ring" (see the image below), thus it is the minimum required number that we seek.
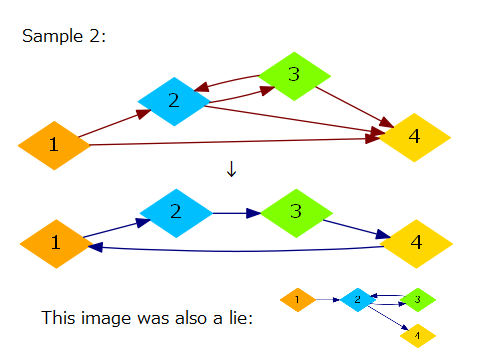
We have found the minimum required number of edges for each wcc in G1 when we do not "merge" them. Let us show that "merging" wccs in G1 do not reduce the number of required edges. Suppose we combine k( > 1) wccs C1, C2, ..., Ck in G1 into one wcc C in G2. Again, there are two cases to consider:
- If none of C1, C2, ..., Ck contains cycles, then C will need |C1| + |C2| + ... + |Ck| - 1 edges. However, if we do not combine them, we will only need (|C1| - 1) + (|C2| - 1) + ... + (|Ck| - 1) edges in total, which is fewer.
- If some of C1, C2, ..., Ck contain cycles, then C will need |C1| + |C2| + ... + |Ck| edges. However, if we do not combine them, we will need
(|C1| - noCycles(C1)) + (|C2| - noCycles(C2)) + ... + (|Ck| - noCycles(Ck) ≤ |C1| + |C2| + ... + |Ck| edges
(here, noCycles(Ci) is 1 if Ci do not contain cycles, otherwise 0), thus combining them does not reduce the number of required edges.
Thus, we do not need to combine multiple wccs into one wcc in G2 in order to obtain the optimal solution. That is, the final answer to the problem is the sum of the minimum required number of edges for each wcc in G1, when they are considered separately.
As for the implementation, detecting cycles in a directed graph with 105 vertices and edges might be a problem if this is your first encounter with it. One possible way is to paste a code that decomposes a graph into strongly connected components. If the size of a strongly connected component is more than one, then that means the component contains cycles.
The writer's code (strongly connected component decomposition, C++): 9501202
Div.2 E / Div.1 C: 505E - Mr. Kitayuta vs. Bamboos
[Problem] Since it is hard to summarize this problem, please refer to the official statement.
(Problem from yosupo)
Below is the explanation from yosupo, translated by me.
[From here]
Let us begin by applying Binary Search. The problem becomes: "is it possible that all the bamboos are at most X meters after m days?" It is complicated by the fact that the height does not become negative; the excessive decrease will be wasted. We have found two approaches to this problem.
- Solution 1
Mr. Kitayuta must beat the i-th bamboo at least max(0, ⌈(hi + m·ai - X) / P⌉) times (let this number ti). Actually, it is not necessary for him to beat it more than this number of times. Thus, let us assume that he beat the i-th bamboo exactly ti times. Also, for each j (1 ≤ j ≤ ti), find the day di, j such that, if the j-th beat on the i-th bamboo is performed before day di, it will be no longer possible to keep the i-th bamboo's height after m days at most X (it can be found by doing simple math). If Mr. Kitayuta can beat the bamboos under this constraint, all the bamboos' heights will become X meters or less after m days. Otherwise, some bamboos' heights will exceed X meters.
The time complexity of this solution will be 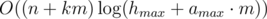 , if we first calculate only ti, then if the sum of ti exceeds km, we skip finding di, j (the answer is "NO").
, if we first calculate only ti, then if the sum of ti exceeds km, we skip finding di, j (the answer is "NO").
- Solution 2
This problem becomes simpler if we simulate Mr. Kitayuta's fight backwards, that is, from day m to day 1. It looks like this:
[Problem'] There are n bamboos. At the moment, the height of the i-th bamboo is X meters, and it shrinks ai meters at the beginning of each day. Mr. Kitayuta will play a game. He can use Magic Hammer at most k times per day to increase the height of a bamboo by p meters. If some bamboo's height becomes negative at any moment, he will lose the game immediately. Also, in order for him to win the game, the i-th bamboo's height must be at least hi meters after m days. Is victory possible?
Below is an illustration of this "reverse simulation":
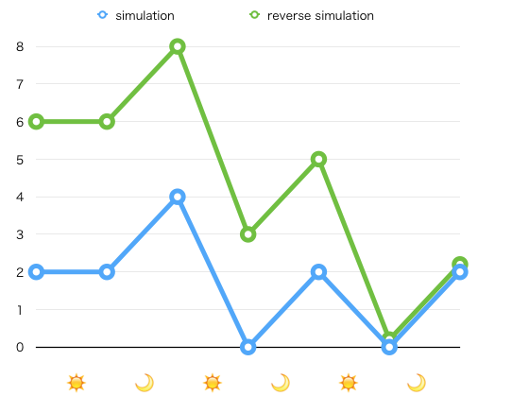
This version is simpler because he is increasing the heights instead of decreasing, thus we do not need to take into account the "excessive decrease beyond 0 meters" which will be wasted. Let us consider an optimal strategy. If there exist bamboos whose heights would become negative after day m, he should beat the one that is the earliest to make him lose. Otherwise, he can choose any bamboo whose height would be less than hi meters after day m. Repeat beating the bamboos following this strategy, and see if he can actually claim victory.
The writer's implementation of this solution uses a priority queue, and its time complexity is 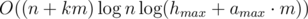 .
.
[End]
The tester's code (Solution 1, C++): 9501229
The writer's code (Solution 2, C++)
Div.1 D: 506D - Mr. Kitayuta's Colorful Graph
[Problem] Given an undirected graph whose edges are painted in colors, process the queries of the following form:
- Given two vertices ui and vi, find the number of the colors that satisfies the following condition: the edges of that color connect ui and vi (possibly indirectly).
Note: this is the exact same problem as Div.2 B except the constraints, which are 105 instead of 100.
(Problem from hogloid)
Below is the explanation from hogloid.
[From here]
For each color, make a new graph that consists of the edges of the color and vertices connected by the edges. Make UnionFind for each graph, and you can check whether a color connects vertex A and B , using it. For each query, find a vertex which has smaller degree(let this vertex A, and the other vertex B) For each colors such that a edge of the color connects to A, check whether A and B is connected by the color. After answering the query, memorize its tuple — (A, B, answer). If the same query is requested, answer using this information.
This will lead to 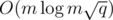 solution.
solution.
For each query, the complexity is 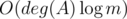 (For each color connects A, find a vertex of B of the color & check whether they are connected) The queries that require longest computing time are, to ask every pair among
(For each color connects A, find a vertex of B of the color & check whether they are connected) The queries that require longest computing time are, to ask every pair among 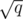 vertices which have largest degrees. Let the indices of the
vertices which have largest degrees. Let the indices of the 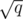 vertices be
vertices be 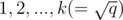 , and degrees of the
, and degrees of the 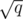 vertices be d1, d2, ...dk. Now, let's fix vertex B as i. The total computing time of the queries such that B is vertex i is
vertices be d1, d2, ...dk. Now, let's fix vertex B as i. The total computing time of the queries such that B is vertex i is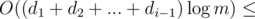
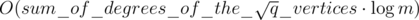 .
.
Vertex B can vary from 2 to k. Hence, the total complexity is at most 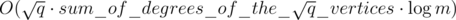 . This complexity is at most
. This complexity is at most 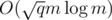 .
.
By the way, in C++, using unordered_map, total complexity would be 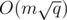 .
.
[End]
There will be many other solutions. I will briefly explain one of them which I think is typical.
Let ci be the number of colors of the edges incident to vertex i. The sum of all ci does not exceed 2m since each edge increases this sum by at most 2. Thus, there will be at most 450 values of i such that ci ≥ 450 (let B = 450). We will call these vertices large, and the remaining ones small. Using O(m / B·m) = O(m2 / B) time and memory, we can precalculate and store the answer for all the possible queries where at least one of ui and vi is large, then we can immediately answer these queries. For the remaining queries, both ui and vi will be small, therefore it is enough to directly count the color that connects vertices ui and vi in O(B) time. The total time required will be O(m2 / B + Bq). If we choose 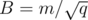 , we can solve the problem in
, we can solve the problem in 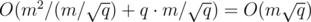 time.
time.
The writer's code (the first solution, C++)
The tester's code (the second solution, C++): 9501240
Div.1 E: 506E - Mr. Kitayuta's Gift
[Problem] Given a string s and an integer n, find the number of the palindromes that can be obtained by inserting exactly n letters into s.
Note: Div.2 A is a similar problem, where n is fixed to 1.
(Problem from evima)
First of all, let us note that we are asked to count the resulting palindromes, not the ways to obtain them. For example, if we are to insert "b" into "abba", there are 5 possible positions, but only 3 strings will be produced ("babba", "abbba" and "abbab"). Rather than trying to count the ways of inserting a letter n times and removing the duplicated results, we should directly count the resulting palindrome. To do that, let us reformulate the problem:
[Problem'] Given a string s and an integer n, find the number of the palindromes of length |s| + n (let this number be N) that contains s as a subsequence (not necessarily contiguous).
Consider constructing a palindrome from both ends, and matching it to s from both left and right. For example, let s = "abaac" and N = 11. Let us call the final resulting string t. We first decide what letter to use as t1 and t11 (they must be equal in order for t to be a palindrome). Let us say 'c' is chosen. Now, we have to construct the remaining part of t, that is, t2..t10, so that t2..t10 contains "abaa" as a substring (note that the 'c' at the end of s is discarded). Again, we decide what letter to use as t2 and t10. This time we choose 'a'. Then, we have to construct t3..t9, so that it contains "ba" as a substring (this time the two 'a's at the both ends of s are discarded). We choose t3 = t9 = 'c'. Next, we construct t4..t8, so that it contains "ba" as a substring (this time s remains unchanged). We choose t4 = t8 = 'b'. Then, we construct t5..t7, so that it contains "a" as a substring. We choose t5 = t7 = 'a' (it is becoming repetitive, isn't it?). The last part of t, that is, t6, has no restriction (this time we choose a letter for only one position of t, not two). We choose 'd', and we have obtained a palindrome "cacbadabcac" that contains s = "abaac" as a subsequence.
This problem is mostly about analyzing this process carefully.
The most naive solution other than literally enumerating all palindromes of length N would be the following Dynamic Programming: let dp[i][left][right] be the number of the palindromes t that can be obtained if you have already decided the leftmost and the rightmost i letters (2i in total), and the substring sleftsleft + 1..sright of s remains unmatched. Each value in this table can be computed in O(1) time. Of course, since i can be up to ⌊n / 2⌋ (n ≤ 109), this solution is far from our goal.
Notice that the transitions from dp[i] to dp[i + 1] are the same regardless of i, thus we can calculate the table by matrix exponentiation. However, since there are O(|s|2) possible pairs for (left, right), we will need 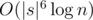 time, which is actually worse than the naive calculation considering that |s| can be up to 200.
time, which is actually worse than the naive calculation considering that |s| can be up to 200.
This is where we need to observe the process which we have gone through at the beginning more carefully. Let us build a automaton corresponding to the process (the image below).
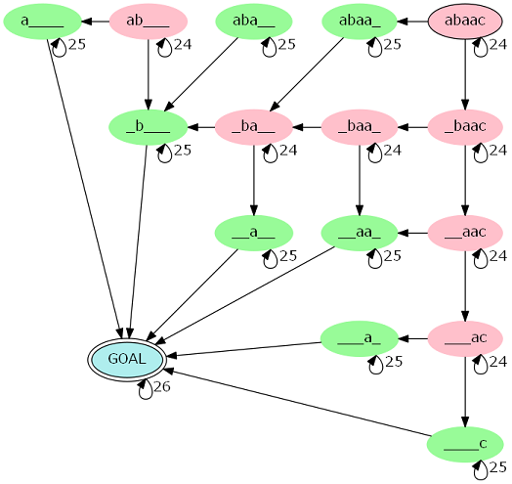
(*) An self-loop with a number means that there are actually that number of edges.
A process of producing a palindrome of length N that contains s as a subsequence corresponds to a path of length ⌈N / 2⌉ from the upper-right vertex to the lower-left vertex. Each red vertex has 24 self-loops since the letters at the both ends of the remaining part of s is different, which correspond to two non-self-loop transitions. Similarly, each green vertex has 25 self-loops since the first letter and the last letter of the remaining string is the same, and the blue vertex, the destination, has 26 self-loops, as there are no more non-self-loop transitions available.
Here is an important fact: there are not so many possible combination of (n24, n25), where n24 and n25 are the number of times a path from START to GOAL visits a red vertex (with 24 self-loops) and a green vertex (with 25 self-loops), respectively. Why? Each time we leave a red vertex, the length of the remaining unmatched part of s decreases by 1, since exactly one of the two letters at the ends of the remaining part is matched and discarded. Similarly, each time we leave a green vertex, the length of the remaining string decreases by 2, since both of the two letters at the ends are matched and discarded. There is a exception, however: if the length of the remaining string is 1, then it will be a green vertex, but in this case the length will decrease by 1. Thus, for any path from START to GOAL, n24 + 2·n25 will be equal to either |s| or |s| + 1. If we fix n24, then n25 will be uniquely determined by n25 = ⌈(|s| - n24) / 2⌉. Since n24 can only take the value between 0 and |s| - 1, there are at most |s| possible pairs of (n24, n25).
With this fact, we are ready to count the paths: let us classify them by the value of n24. For each possible pair of (n24, n25), let us count the number of corresponding paths. To do that, we divide each paths into two parts: first we count the number of paths from START to GOAL, using only non-self-loop transitions. Then, we count the ways of inserting self-loop transitions into each of these paths. The product of these two numbers will be the number that we seek.
The first part is straightforward to solve: let dp[left][right][n24] be the number of paths from the vertex that corresponds to the substring sleftsleft + 1..sright, visiting exactly n24 red vertices using only non-self-loop transitions. Each value of the table can be found in O(1) time, thus the whole table can be computed in O(|s|3) time, which is fast enough for the input size (|s| ≤ 200).
The main obstacle will be the second part. For example, let us consider the case where s = "abaac", N = 11, n24 = 2, which corresponds to the example at the beginning. From the fact we found earlier, n25 = ⌈(|s| - n24) / 2⌉ = ⌈(5 - 2) / 2⌉ = 2. Thus, we have to insert ⌈N / 2⌉ - n24 - n25 = 6 - 2 - 2 = 2 self-loop transitions into this path (the image):

The order in which red, green and blue vertices appears in this path does not affect the number of ways of insertion, and can be arbitrary. The number of ways to insert 2 self-loop transitions will be equal to the number of the path of length ⌈N / 2⌉ = 6 from START to GOAL in this automaton (we have to take into account the non-self-loop transitions in it), which can be calculated by matrix exponentiation.
Are we done? No! Consider the case s = "abbb..(|s| - 1 times)..bb". There are |s| - 1 possible values of n24 (n24 = 1 corresponds to the case where you match and discard the 'a' first, and n24 = |s| - 1 corresponds to the case where you keep the 'a' until s becomes "ab"). Thus, you need to perform matrix exponentiation |s| - 1 times, which results in a total of 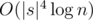 time, which will be too much under the given constraints.
time, which will be too much under the given constraints.
There is still hope, though, and here is the climax. Notice that these automata are very similar to each other, and they differ only in the number of the red and green vertices. We can combine these automata into one larger automaton like this (the image):
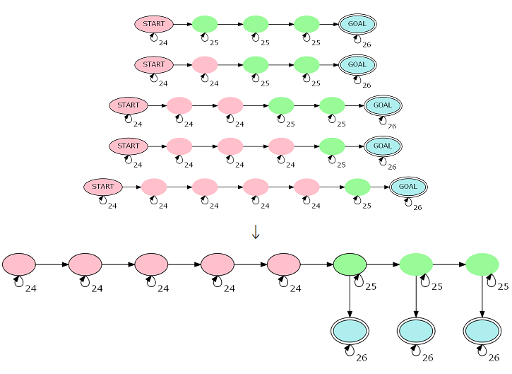
The combined automaton should have |s| - 1 red, ⌈|s| / 2⌉ green and ⌈|s| / 2⌉ blue vertices.
By performing matrix exponentiation on this automaton instead of many small automata, we can find all the required value in 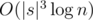 time, which should be enough. We recommend speeding up matrix multiplication by noticing that the matrix will be upper triangular (6 times faster on paper), since the time limit is not so generous (in order to reject
time, which should be enough. We recommend speeding up matrix multiplication by noticing that the matrix will be upper triangular (6 times faster on paper), since the time limit is not so generous (in order to reject 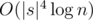 solutions).
solutions).
The problem is almost solved, but there is one more challenge. When N is odd, the situation becomes a little complicated: as we have seen at the beginning, in the last (⌈N / 2⌉-th) step of producing a palindrome we choose a letter for only one position of the resulting string, that is, the center of that string. In other words, the last transition in the path in the automaton we have first built must not be one from a green vertex with a string of length 2 (for example, "aa") to GOAL.
Let us find the number of the paths that violates this condition and subtract it from the answer. As previously mentioned, for each path n24 + 2·n25 will be equal to either |s| or |s| + 1, and if we fix the value of n24, n25 will be uniquely determined by n25 = ⌈(|s| - n24) / 2⌉. If |s| - n24 is odd, then it means that the last non-self-loop transition is one from a green vertex with a string of length 1, therefore in this case no path will violate the condition. If |s| - n24 is even, then the last non-self-loop trantision is from a green vertex with a string of length 2, thus the paths that does not contain the self-loop from GOAL to itself violate the condition. It will be equal to the number of the paths of length ⌈N / 2⌉ - 1 from START to the vertex just before GOAL, which can be found in a similar way to the second part of the solution.
The journey has finally come to an end. Actually, it is also possible to solve this problem in 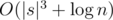 time without matrix exponentiation, but this margin is too small to explain it. I will just paste the link to the code.
time without matrix exponentiation, but this margin is too small to explain it. I will just paste the link to the code.
The writer's code (matrix exponentiation, C++): 9501164
The writer's code (without matrix exponentiation, C++): 9501177
Congratulations again to Petr who was the only participant to solve this problem in 108 minutes. Also, I would like to give a special mention to rng_58, who was VERY close to solving it in only 63 minutes. He was just one byte away from getting AC (compare 9460984 and 9465440)!
If you find a possible error, or have a question, please feel free to ask here. Alternative solutions are also welcome.











Div 1 B is one of the best Codeforces problems that I've seen. Kudos to the setters! :D
Thank you, we are so happy to hear that! It seems that although we failed miserably in expecting the difficulty of the problems, we did not fail too much in making problems itself.
A difficult contest once in a while is actually good in my opinion.
I must say I did not take part at your contest (uncomfortable schedule), but I've solved A and B at the moment and I found them enjoyable (and I've laughed a lot with "the image is a lie", even if it disoriented me at the beginning).
Also, from the very short experience I have setting problems, I think that (objective) difficulty estimation is not an easy task, in fact, I think it could be harder than preparing, solving and testing the problem itself.
after seeing your comment I've tried it and really it's an awesome problem. Thank you and also a lots of thanks to setter :)
An alternative way to make the dp feasible in Div1A is to use brute force when the first jump is very large. Define very large to be 2000. Then the brute force would have maximum depth of 16, and about 3^16 (43M) operations. When less than 2000, dp[30001][2000] would fit into time and memory.
Yes!! I did this in the same way you have explained! But In this way, Among addition of 3 length, l-1,l,l+1 one shouldn't call the function of length l-1 first. I have got many accepted code failed on a test case I have made! The program stop executing because of stack capacity since function calling with the length l-1 don't bring any solution. My function have called above 16000 times without return any value in any call and have stopped for stack capacity! It was indeed a tricky problem!!! Smart Setters :)
Also want to say about alternative solution of 506D - Mr. Kitayuta's Colorful Graph. Let's enumerate all connected components somehow. By connected components I mean graph where all edges are the same color and it is possible to get from every vertex to each other. We calculate for every vertex all connected components which it belongs. Will store this information using the idea of bitmasks. So for each vertex it's M / 64 64-bit numbers maximum. The answer for each pair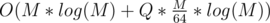 (log for maps). Fortunately it passed by time (CF servers are really fast :) ). Submission: 9463715.
(log for maps). Fortunately it passed by time (CF servers are really fast :) ). Submission: 9463715.
(x, y)will be count of bits incomponents[x] & components[y]. The complexity seems to beOn Div2 C instead of doing the dp bottom-up I did it top-down with memoization, so that the length of the previous jump would never reach d — 245 or d + 245. Why was this way too slow?
It should be fine, for example the Div. 1 winner ilyakor took that approach (9456356: 374ms, Java).
It should be noticed that this editorial has so far been really detailedly written. So no wonder we have to wait for long to see the complete version.
my code is giving correct output for Div 2 a problem (test case-4) but still getting a verdict "WRONG ANSWER" . can anyone please tell the reason. submissionn no. 9484889
It seems that your code outputs a null character at the end of "NA" on test 4, which is unfortunately not acceptable.
P.S. Two participants in the Div. 2 contest sent us similar messages.
In problem 506D, could someone please explain how did the square root of q end up in the complexity? Won't we have to process all q queries to get the right answer?
To be precise, the complexity is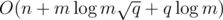 or something, but probably hogloid omitted insignificant terms.
or something, but probably hogloid omitted insignificant terms.
Okay, but I still don't understand how square root of q came into the picture.
Got the error.
I just barely got my code accepted. Here is my code. I made a union find structure for each graph and memoized results but I have seen some people getting ridiculously fast speeds! Is it because of constant optimization? Also I still don't understand how the complexity in the editorial contains a factor of square root of 'q'.
Any help/hint will be appreciated! Thanks!
We are looking at the worst case, which is when all q queries are only within the sqrt(q) vertices with the biggest degree. For each vertex you have sqrt(q) qeuries with it, which summarized complexity is the sum of the degrees of the sqrt(q) vertices with the biggest degree, which isn't greater than m. You have sqrt(q) vertices, so the complexity is sqrt(q)*m. It can't be smaller, because if you have 3000 vertices everyone connected with each other and 90000 queries you'll have approximately 90000*300 operations.
Nice editorial :)
I have a question about Div.1 C Solution 1. Why it is not necessary for him to beat bamboo i more than ti times? It is better to beat the bamboo later than earlier, but what if on the later day, k times is not enough? Why we can't beat some bamboo earlier, though they are beat more than ti times, to save times for later days?
First, you assume the number of bamboos is 1. If you hit the bamboo in d_1, d_2, d_3, ..., d_t(1 <= d1 <= d2 <= d3 ... <= d_t <= m, t > ti) and the length of bamboo is no greater than X in last, you hit the bamboo in d_2, d_3, ..., d_t and the length of bamboo is also no greater than X in last. we let D={d_1, d_2, ..., d_t}, and D'={d_2, d_3, ..., d_t} If there are some i(i=2,...,x) that the length of bamboo is 0 after d_i in D', the length of bamboo is 0 after d_i in D, so the length of bamboo is no greater than X in last. If there are not some i, sum of length of magic hammer decrease is no less than (t-1)*P, and (t-1)*P >= ti*P >= h_i + m*ai — X.
I think the idea of converting the problem used in solution 2 to Div1.C is great because it avoids the waste of height decreased. I would like to share my thoughts on why it can be converted to such a new problem.
We just need to consider the case where there is only one bamboo. Consider any scheme in the original problem. When you waste for the first time, which corresponds to a segment intersecting with the horizontal line y = 0, you can just move the footprints in the past upwards to make them all above or on y = 0. Notice that this guarantees that all the footprints are not below y = 0, and you move footprints only upwards. Besides, it is obvious that when you are about to make the (i + 1)st footprint, it is sure that the i-th footprint is at the correct position. That suggests the final point, which is required to be below y = k, is finally at its correct position in spite of the moving operation. So we can see that every scheme in the original problem corresponds to a scheme in the new problem.
Now consider a scheme in the new problem. If the position of the first footprint is (0, x), then x ≥ h must be satisfied. Let d = x - h. Then try to move the footprints downwards by d. When they have moved by d' < d, and there are footprints on y = 0, just find the leftmost one, say chronologically the i-th, and iteratively try to lower the footprints from 0 to i — 1 by d - d'. Finally we can see the first footprint becomes (0, h), and the last footprint is still not above y = k. Thus every scheme in the new problem corresponds to a scheme in the original problem.
Then we know the two problems are equivalent.
@evima "Note: For some strange reason, we (contest managers) cannot submit solutions so that everyone can see them. "
When I authored my first contest, I overcame with this problem by submitting solutions of all the problems specifically from the section problemset rather than by going through the contest tab.
It worked. Thank you for the information!
In divion 1 B suppose there are 4 nodes and 5 edges as stated below - 1->2 2->3 3->1 1->4 4->3 then the minimum number of edges required is still 5 but my code gives 4 ..or am i missing something?
If the number of nodes is n, then n edges are always enough, since you can connect all cities into a "ring" (1 → 2, 2 → 3, ..., n → 1).
In the above case of 4 nodes with 5 edges 1->2,2->3,3->1,1->4,4->3...the cycle is of the form 1->2->3->4->3->1 .... so we need all the 5 edges
Quote from the problem statement: "He is planning to construct teleportation pipes so that for each important pair (ai, bi), it will be possible to travel from city ai to city bi by using one or more teleportation pipes"
For Div1 B, Can someone please give explanation for this case
Please note that Mr. Kitayuta's objective is to make it possible to travel from city ai to city bi by using one or more teleportation pipes.
Thanks .. :) Got it :)
In the solution code of Div 1B, what is the purpose of dfs2() ? can anyone please let me understand.
Hi, maybe you have already understood the purpose of dfs2 but anyway...
It goes searching a vertex which belongs to a SCC that has more than one vertex, if it found it return 0 ( its a wcc which has a cycle ) otherwise it returns 1 ( its a DAG, so it's just necessary V-1 edges ) . dfs2 goes through edges not considering their directions thats wy call dfs2 two times ( for g and rg )
Could you clarify the phrase:
I cannot understand how to compute dij. We don't know the current height of the bamboo, when we perform the j-th beat. How can we understand wether it's possible to finish with <= X or not?
In tester's (evima) Solution 9501229, For Problem C Div1 (Problem E for Div2).. Can someone please explain this conditions a more elaborately,
I'v read the editorial many times, but I can not figure out the logic behind these conditions. Thanks in advance :)
http://codeforces.com/contest/505/submission/13238470
could anyone help me to find bugs in this code?
hi acmer first thanks for these nice problems second, in problem ( DIV 1A ) ( https://ideone.com/GLXkVj) why you write : int jj = j-(d-250); and thank you (yosupo).
Problem Div.2 B can also be done with simple Floyd Warshall :D http://codeforces.com/contest/505/submission/40466126
I think so, and i use the bitset ,it's so faster https://codeforces.com/contest/505/submission/72992634
Is there anyway better to solve Div2-B ?
I think .... $$$q\cdot k \cdot n$$$
How to solve Div2A Mr. Kitayuta's Gift using Matrix Power methods? It's in the A2OJ list item 13. I know the intended solutions, but I'm curious to know this approach.