100589A - Queries on the Tree
Given a rooted tree(at node 1) of N nodes,you have to handle a total of Q operations of type:
1 U L X: Increase coins by X of all nodes at a distance of L from root.
2 X: Report sum of all coins in subtree rooted at X.
N <= 105 Q <= 104
Difficulty:
Medium-Hard
Explanation:
This approach uses a very specific technique of maintaining a buffer of update queries and updating the whole tree once buffer size exceeds a constant limit(we maintain this limit as sqrt(M)).
buffer=[]
q=input
while q--:
query = input()
if query==update:
buffer.add(query)
else:
//say query is “2 X”
//the answer that has been already calculated for node X
prevans= ans(X)
for i=0 to buffer.size():
//add to prevans the effect of buffer[i]
//let’s say buffer[i]=”1 U L Y”
//if buffer[i] affected K nodes in subtree of X
//we add to prevans: K*Y
//so, we need to count how many nodes of subtree X
//are at a level L, we’ll show later how to handle this
print prevans
if buffer.size() > sqrtM:
//update the whole tree and precalculate answer of all nodes
So, we need to look at two things:
Given X and L count how many nodes in subtree of X are at a level L(this level is measured from root).
For this we first DFS transform our tree such that all nodes in a subtree lie in contiguous range after new mapping(according to DFS). And then we maintain for each level an array which stores the new indexes of all nodes that are at that level.
For example, a vector level[L] stores all new indexes of nodes that are at level L. These vectors can easily be made in O(N) by a DFS.
Now, for a query “Given X and L count how many nodes in subtree of X are at a level L”, we know the range of new indexes of all nodes in subtree of X(say the range is S to R), we just have to count number of values in vector level[L] that lie in range [S,R], which can be done in O(log N) worst case.Given at-most sqrt(M) queries of type “L X”,(which denote update X at all nodes at level L), we have to update the whole tree.
We traverse over all queries and mark in a count array(**count[i]** contains the total coins to be updated at level i). Now, while doing a DFS of tree we can easily update the current_sum on each node. And then to pre calculate answers for each node we do one more DFS.
So, we don’t update our tree more than sqrt(M) times and each update takes O(N). Also, for print queries we don’t process more than sqrt(M)*log(N) worst case. So, a loose upper bound on total complexity will be O(N * sqrt(M) * log N).
Many problems can be solved by this specific technique of making buffers of queries. For example this problem: 447E - DZY Loves Fibonacci Numbers
100589B - Count Palindromes
To find the number of palindromes which appear between two instants of time when seen on a digital clock. Upto 105 queries.
Difficulty:
Easy
Explanation:
The number of distinct strings which one can see are 86400(from 00:00:00 to 23:59:59). Answering each query, would take O(86400 * 6) in the worst case. And there are 105 queries.
So, we can initially pre process for all possible times.
Let the time is ab:cd:ef then converting it to seconds s = ab*24*60 + cd*60 + ef.
As 1 hour = 60 minutes and 1 minute = 60 seconds.
X[s] denotes if s is a palindrome or not.
Now we maintain a prefix sum array so as to answer all queries in O(1).
MX = 86400 + 1
for i in xrange(0, MX) :
mem[i] = 0
mem[0] = 1
for i in xrange(1, MX) :
val = conv(i)
mem[i] = mem[i - 1]
if Palin(val) :
mem[i] += 1
Let mem[i] denote the number of palindromes from 0 till i.
conv is a function which converts a number x to string of length 6. Appends leading zeroes till the size is 6. Palin is a function which returns True or False depending on whether the given string is a palindrome or not.
Now for each query, we convert the given time to seconds. Let the converted times into seconds be a, b. The number of palindromes between a and b are
mem[b] : if a = 0
mem[b]-mem[a-1] : else
100589C - Find P'th Number
Given N and P, Either all even or all odd numbers have been removed from set [1, 2, 3 ... N], find the Pth smallest remaining number.
N <= 109
Difficulty:
Cakewalk
Quick Explanation:
Answer is either 2 * P(if all odd are removed) or 2 * P — 1(if all even are required, one less than in other case because instead of 2 we report 1, 3 instead of 4 and so on).
100589D - Desolation of Smaug
Note : Since there are N nodes and N edges in the graph, the graph would be like a tree containing a single cycle (because a tree with N nodes has N-1 edges. On adding an edge in the tree , wherever we might add the edge, we shall always get a single cycle in the graph) . Imagine the given graph as a cycle with a tree hanging down at each node. This is a special property of a graph with N nodes and N edges which must be exploited to answer the queries in sublinear time.
Explanation
Once again we have many interesting things to observe in this question . Lets start by analyzing each part one by one.
First, What does the question ask us to do?
The problem statement is short and precise . Frodo needs to escape from Smaug. Given the initial positions of both and the destination of Frodo along with the velocities of both, print YES or NO depending on whether Frodo can escape or not. Sounds easy, a simple dijkstra once from Frodo and once from Smaug would get us the answer. But, then comes the interesting part, Q queries where Qmax = 105. Following the Dijkstra approach for each query will be O(Q * N logN) which undoubtedly would fetch us TLE.
So what to do?
Seeing the constraints, it is clear that we need to do some linear pre-processing on the given graph such that we can answer each query in sublinear time.
But before directly jumping to the implementation and seeing how to achieve the task of answering the queries in sublinear time, let us first do a theoretical analysis of the problem to completely understand what we need to do and then we shall focus on how to do it.
Theoretical Analysis
As explained in the note above, we need to imagine the given graph as a cycle with a tree (possibly with only a single node, the root) hanging down at each node in the cycle. (See diagram on below).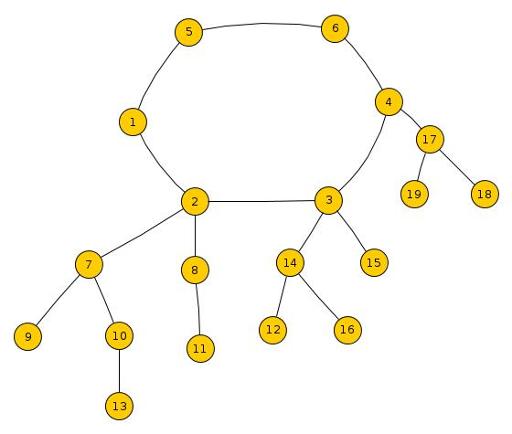
Now, let’s analyze the various possible cases based on the parameters which vary in each query, i.e. Vf, Vs, St, Ds, S.
Case 1: Vs >= Vf
We just need to check who reaches the destination(**Ds**) first, Frodo or Smaug because if Smaug can catch Frodo at some node on the way to destination , he can definitely catch him at the Destination . Hence
If(Dist(St,Ds) * Vs< Dist(S,Ds)*Vf) //Or Dist(St,Ds)/Vf < Dist(S,Ds)/Vs
print "YES";
else
print "NO";
Case 2: Vs < Vf
In this case , if Frodo escapes/ gains lead over Smaug at any node, Smaug cannot catch him and Frodo is gone forever . To better understand this, let us visualize the various possible cases that arise based on different locations of St, Ds, S.
Sub-Case 1 : All Three St, Ds, S lie in the same tree and S lies within the subtree rooted at LCA(St, DS).
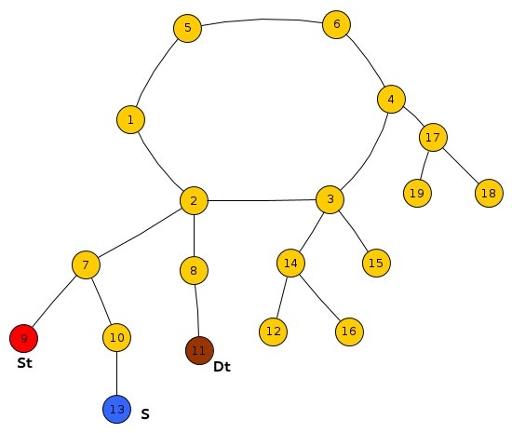
As shown in the diagram, if Frodo escapes Smaug at node 7, i.e. Frodo reaches before Smaug at node 7, he can safely reach Dt else he will surely get caught by Smaug at node 7.
In general, we compare the reaching time’s of Frodo and Smaug at the min(LCA(St,S),LCA(S,Dt)).
where min() represents the lower one(the one with greater level down the root) of the two because in each case, one of the above two will always be equal to LCA(St,Dt).
Sub-Case 2 : Both St, Ds lie in the same tree and S lies outside the subtree rooted at LCA(St, DS).
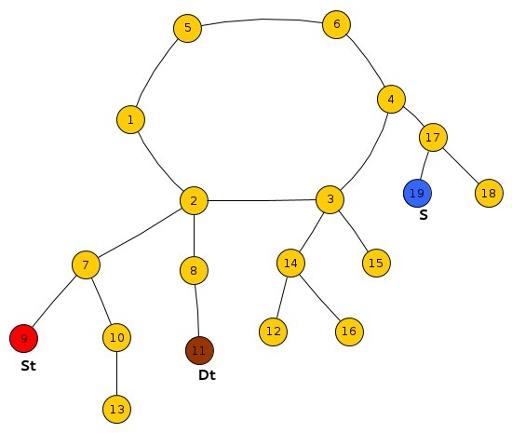
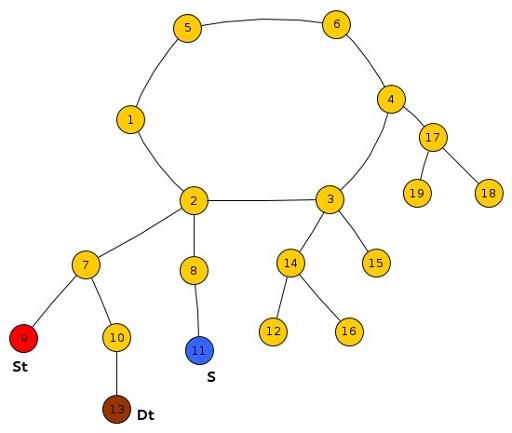
We just need to compare the reaching time of Frodo and Smaug at the LCA(St,Dt) s.t.
if(reachingTime[Frodo][LCA(ST,DT] < reachingTime[Smaug][LCA(St,Dt])
printf "YES"
else
printf "NO"
Sub-Case 3 : One of St or Dt and S lie in the same tree and the remaining lies in another tree.
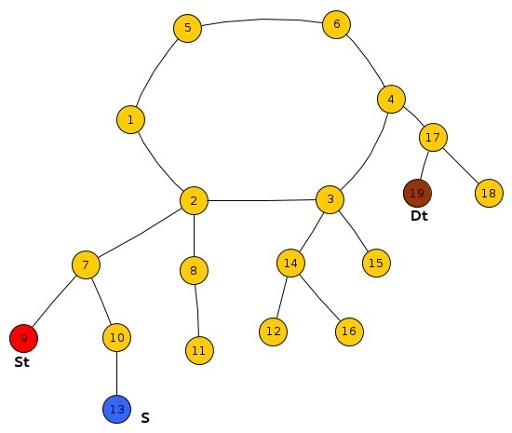
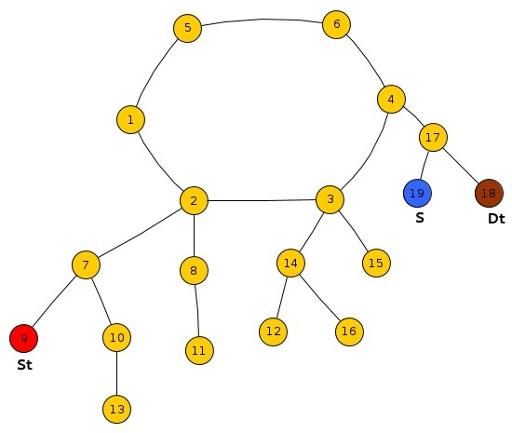
We compare the reaching time of Frodo and Smaug at the LCA(St,S) or LCA(Dt,S) depending on which of St or Dt is in the same tree as that of S. If Frodo can reach this node before Smaug, he can reach the destination otherwise he will surely get caught.
Sub-Case 4 : All three St, Dt, S lie in different Trees.
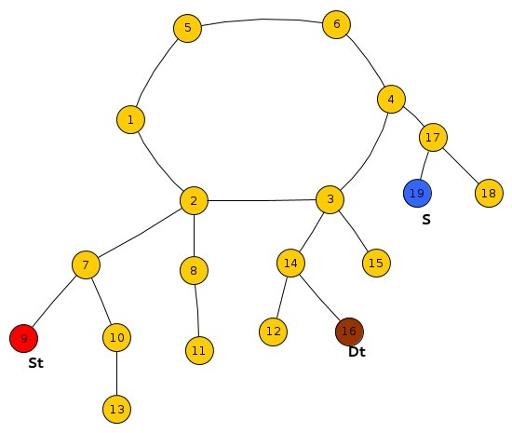
In this case,
First of all, Check whether Frodo can reach the root of his Tree before Smaug. If he can't then no matter what, he will surely get caught at the root of his tree because he definitely needs to pass through that node in order to reach the destination.
If the Smaug cannot catch Frodo at the root of Frodo's tree, we will check whether Frodo can cross the root of Tree of S before Smaug reaches there and if he can, he shall surely escape.
If Smaug can catch Frodo at the root of S, we’ll compare the time taken by Frodo to reach the root of tree of Dt along the path not involving root of tree of S and the shortest time taken by Smaug to reach the root of Dt.
If time taken by Frodo is less than that of Smaug, Frodo shall escape or else he will get caught.
How to Implement?
Well, If you’re still alive and reading this editorial, Congratulations because we’ve reached the final part. :P
In the above Theoretical analysis, we made use of two functions :
LCA(A,B) : Returns us the Lowest Common Ancestor of two nodes A and B in the same tree.
Dist(A,B) : Returns us the distance between any two nodes A and B in the whole graph (not necessarily in the same subtree).
To handle the Sub-Case 4 under Case 2, we would need to maintain the prefix sum of the path along the cycle because for the cycle, we need to analyze both the clockwise and anticlockwise paths for Frodo depending on conditions mentioned above.
We’ll need shortest distance between any two nodes in the graph in logarithmic time.
Shortest distance between any two nodes in the graph:
For answer these types of queries, first we understand that given graph has a single cycle ie. trees are hanging from nodes in cycle.
So, first we detect the cycle* and then for each tree hanging at a cycle node we build the LCA DP table so that we can handle LCA queries in logarithmic time.
Also, for each such tree we pre-calculate that distance from root node(ie. cycle node) to tree node.
We can do this by a linear order DFS. Let’s call such array dist_root.
*For detecting cycle two methods are:
1. Store indegree of all nodes first and keep removing all nodes from set [1,2,..N] if indegree of node is 1(ie. keep removing leaf nodes). If indegree of any neighbor reduces to 1, remove it. All remaining nodes will be in cycle. We can easily do this using queue in a similar way to BFS.
- Do a DFS and whenever detect a back edge, all vertices currently in recursion stack are cycle nodes.
Now, for distance between node u and v, there are two case:
u and v are in same tree(tree that hangs by a cycle node):
Shortest distance is dist_root[u] + dist_root[u] — dist_root[lca(u,v)].
u and v are in different trees(trees that hangs by two distinct cycle nodes):
Shortest distance is dist_root[u] + dist_root[u] + min-distance(root[u], root[v]).
So, we need to find minimum distance between any two nodes in cycle. First let’s say we map all cycle nodes(say total of K) values 1 to K. Now we pre-calculate a prefix sum array of array A where A[i] stores distance between node 1 and node i(if we travel by clockwise direction).
Now, for min distance between a and b(two cycle nodes):
Let’s say
K = total length of cycle
//assuming mapping[a] > mapping[b]
M = prefix_sum[a] - prefix_sum[b]
min distance = min(M, K-M)
So, we can handle overall min distance queries in worst case O(log N).
100589E - Count Distinct Sets
See the doc: https://docs.google.com/document/d/1-znOOxmNIhcUQNiW8uOQpKUNzFiN2PCt6uY-6nLjIDU/edit?usp=sharing
100589F - Count Ways
Given a grid of size N x M, where K given cells are blocked. Find number of ways to reach (N, M) from (1, 1) if you can move right or down.
N, M <= 105 K <= 103
Difficulty:
Medium-Hard
Explanation:
First a basic formula, number of ways to reach (x2, y2) from (x1, y1) if x2 >= x1 and y2 >= y1:
Let x = x2-x1-1 and y = y2-y1-1
Number of ways F(x1, y1, x2, y2) = (x+y)!/(x!y!) where n! denotes n factorial.
Now, an interesting observation is that if I block a cell at (i, j) all cells with their respective coordinates greater than or equal to i and j will be affected by it(ie. number of ways to reach them will be changed).
Let's say our set S = {all blocked cells + cell(N, M)}. I now sort S on increasing basis of x coordinate and then increasing on y. Also I maintin an array ans where ans[i] denotes number of ways to reach cell at index i in sorted(S).
Intially ans[i] = F(1, 1, S[i].x, S[i].y).
Now, I traverse the sorted(S) in increasing order and updating the number of ways for all the cells that it affects.
for i=0 to S.size()-2:
for j=i+1 to S.size()-1:
if S[j].x<S[i].x or S[j].y<S[i].y: //cell j not affected
continue
//ans[i] stores current number of ways to reach that cell
//now all paths from cell (1,1) to cell j are blocked
//so we subtract (number of ways to reach i * number of paths from i to j)
ans[j] -= ans[i]*F(S[i].x, S[i].y, S[j].x, S[j].y)
print ans[S.size()-1]
While making a decrement at ans[j] due to blocked cell i we ignore that there are some other blocked cells in between them(note that we are mutliplying with F(S[i].x, S[i].y, S[j].x, S[j].y)). We ignore them because ans[i] is currently storing valid paths to reach (S[i].x, S[i].y) and all possible paths now that pass through it are blocked. So we subtract each possible comibination from ans[j].
Complexity: O(K2).
100589G - Count Permutations
Given N(<= 15), K (<= N) count in how many permutations of [1,2,..N] no two adjacent elements differ by more than K.
Difficulty:
Easy-Medium
Quick Explanation:
Maintain a DP of mask and last_used, where mask denotes the number of elements already used and last_used denotes the value of number that was just used before current index.
Explanation:
Naive solution would be O(N+1 factorial). But we can use dynamic programming here and try to reduce complexity. But considering that in a permutation each number from 1 to N is used only once, we can’t keep a generalized DP state like “number of permutations of length i ending in j”, because it doesn’t store information about what numbers we have used.
So, we use bitmasks. Bitmask is basically a N bit binary number expressed as a decimal. If i’th bit in mask is marked we assume that we have already used number i somewhere and it is not available for use anymore.
Now, let’s try to form our solution. For placing a number at a certain position, we should know which number was placed before it(because we’ll compare their absolute difference). So in our state we keep two things: mask and last_used, where last_used denotes the number that was used just before current position.
So, let’s denote by DP(mask, last_used) the number of permutations of numbers marked in mask and ending in last_used.
Let’s form recurrences now.
DP(last_used, mask):
ret=0
for all i unmarked in mask:
//we try to place number i at current position
if abs(i-last_used) <= K:
//last_used is now i
//we pass new mask by setting i’th bit in it
ret += DP(i, mask|(1<<i))
return ret
So, we use DP with memoization. So our complexity is number of states multiplied with transition cost.
So total worst case complexity will be: O(N2 * 2N).
100589H - Count Subarrays
Given an array A1, A2 ... AN and K count how many subarrays have inversion count greater than or equal to K.
N <= 105
K <= N*(N-1)/2
Difficulty:
Medium
Quick Explanation:
Maintain two pointers( pt1 and pt2) and increase pt2 until inversions in subarray [pt1, pt2] are less than K. Now all the subarrays [pt1, i] have inversion count > K-1 where i > pt2-1.
Now, we increase pt1 until inversion count in subarray [pt1, pt2] is greater than or equal to K.
And we repeat the above process until we reach end of our array.
Inversion count can be handled easily using BIT.
See detailed explanation for more clarity.
Explanation:
The most important property to be observed it that if there are P inversions in subarray [S, E], the inversions in subarray [S, E+1] will be greater than or equal to P, because the value at index E+1 may contribute some inversions. How many inversions exactly will it contribute? It will be equal to number of elements that are greater than AE+1 in range [S, E].
So, for each index i, if we get the smallest j(let’s call such a value threshold(i)), such that inversions in subarray [i, j] is greater than or equal to K, we know that all subarrays [i, k] are valid(where k >= j). So, our aim is to get this smallest j for each i.
Let’s say we are index i (pt1) initially are we have found the respective j (pt2) for it.
We know that InvCount[i, j] >= K and
InvCount[i, j-1] < K
If I increase i by 1 now, I know that inversion count is going to reduce. After reduction if inversion count is still greater than or equal to K, we know that threshold for i+1 remains same because we know InvCount[i, j-1] < K, therefore InvCount[i+1, j-1] < K is also valid.
Now we keep increasing pt1 until inversion count is not less than K. Once we reach such an index, for this index we need to find it’s threshold, so we start increasing the pt2 until we reach threshold of pt1.
Now, we need to handle two operations. Let’s say we have right now inversion count for range [L, R], we need inversion count for [L, R+1] quickly and similarly for [L+1, R].
So, we use a BIT here. Let’s say in a BIT we have marked all values in range [L, R]. To get inversion count for [L, R+1], we need to count how many values in range [L, R] are greater than AR+1, which can be easily found by BIT(since all elements in range [L, R] are marked in BIT). Once we get new inversion count we also mark the value AR+1 in BIT.
Similarly for [L+1, R], we count how many values in BIT are less than AL. This count will be reduced from the current inversion count. Also, we unmark **AL from the BIT.
But since all values Ai are up to 109 and we only need to compare their greater and lesser(exact values doesn’t matter), we use coordinate compression(ie. map larger values to smaller distinct values). After this we can easily mark any Ai in the BIT.
Pseudo code:
BIT:
getsum(i) //returns sum of of elements with index <=i
update(i,val) //updates val at index i
A=input
rank[i] = rank of A[i] in sorted(A[i])
pt1 = pt2 = 0
BIT.update(1,rank);
cur_inv = 0 //inversions of current subarray denoted by [pt1, pt2]
ans = 0
while pt1<N:
//we increase pt2 until current inversions <K
while cur_inv<K and pt2<N
pt2 ++
//inversion increment due to addition of A[pt1]
//increment = number of elements greater in BIT less than A[pt1]
inv += r + 1 - BIT.getsum(A[pt1])
//add A[pt2] to BIT
BIT.update(A[pt2], 1);
//all subarrays [pt1, x] are valid, where N > x >= pt2
ans += N-pt2
//remove A[pt1] from BIT and reflect the change in cur_inv
// and increment pt1
BIT.update(A[pt1], -1)
inv -= BIT.getsum(A[pt1] - 1)
pt1++
Another way would be to use segtree/trie for queries like "find number of elements in range L to R which are less than K".
100589I - Laughing Out Loud
Given a string S, you have to find out the number of length 3 sub-sequences which are equivalent to LOL. |S| <= 105
Difficulty : Easy
Explanation : Subsequence is a sequence that can be derived from another sequence by deleting some elements without changing the order of the remaining elements.
Assume initial string to be S. If we take a boolean string X of length len(S) (= n).
if we want to include i'th element of S as part of subsequence : X[i] = 1
else: X[i] = 0
Number of different strings X is equivalent to the number of subsequences.
We have a y bit string of 0’s and 1’s.
Let S = “ABA”, then n = 3 and all the y bit strings are as follows
000 ‘’(None, empty string)
001 ‘A’
010 ’B’
011 ‘BA’
100 ‘A’
101 ‘AA’
110 ‘AB’
111 ’ABA’
So, for a sequence of length n, 2n subsequences are possible. Finding all the subsequences would time out.
As we know that we only have to find the subsequences of length 3(LOL). A naive code for checking if S[i] = ‘L’, S[j] = ‘O’, S[k] = ‘L’ subject to the condition that 1 <= i < j < k <= n.
ans = 0
for i in xrange(1, n+1) :
if S[i] == ‘L’ :
for j in xrange(i+1, n+1) :
if S[j] == ‘O’ :
for k in xrange(j+1, n+1) : #1
if S[k] == ‘L’ : #2
ans += 1 #3
Complexity of the above code is O(n3) which would time out.
for i in xrange(1, n+1) :
suf[i] = 0
if S[1] == ‘L’ :
suf[1] = 1
for i in xrange(2, n+1) :
suf[i] = suf[i-1]
if S[i] == ‘L’ :
suf[i] += 1
Suppose we maintain a suffix-sum array which tells us the number of L’s after index i till n. As we just to have to find if S[i] == ‘L’ , S[j] == ‘O’ and we know the number of k > j and k <= n is suf[j+1]. For finding answer we replace #1, #2, #3 by ans += suf[j+1]. We can reduce the complexity to O(n2), which would also timeout.
for i in xrange(1, n+1) :
pre[i] = 0
if S[n] == ‘L’ :
pre[n] = 1
for(i = n-1; i >= 1; i -= 1) :
pre[i] = pre[i+1]
if S[i] == ‘L’ :
pre[i] += 1
Similarly maintaining another prefix-sum array which tells the number of L’s from 0 to index i. If we know that S[j] == ‘O’, then pre[i-1] tells us the number of L’s before j and suf[j+1] tells us the number of L’s after j. Answer is the summation of product of suf[j+1] * pre[j-1] such that S[j] == ‘O’.
Complexity of this would be O(n) with a space of O(n), which fits the time limit.
If we consider a string of length (105) such that all the characters are L except the middle character which is O, then the product would not fit in a 32-bit integer data type. But would fit in a 64-bit integer data type. Maximum possible answer would be of the order 1012.
100589J - Three Sorted Arrays
The points to note in the problem are:
1. The arrays are sorted.
2. We need to find all triplets such that i ≤ j ≤ k and A[i] ≤ B[j] ≤ C[k].
In worst case the number of triplets will be in order of O(P*Q*R), hence brute force solution won’t work.
There are two approaches to solve this problem.
Binary Search:
Reducing the problem to finding j ≤ k and B[j] ≤ C[k]. This can easily be done using binary search, for each B[j] we need to find the index of C[k] which is just smaller than B[j], (say index is L) all the values, present in the index greater than L, will be greater than B[j], hence the number of values greater than B[j] are Q-i (assuming 1-based indexing).
The computation time will be Q(log(R)) (for each element we have to do a binary search).
The problem extends to finding i ≤ j ≤ k and A[i] ≤ B[j] ≤ C[k]. We have already found out j ≤ k and B[j] ≤ C[k].
For every A[i] we need to find out the index of B[j] which is just smaller than A[i](say it’s M) all the values, present in the index greater than M, will be greater than A[i] but we also need to find it’s corresponding value in C[k], hence a postfix sum array of the values j <= k and B[j] ≤ C[k] can be used. The example will help in better understanding.
The overall complexity of the algorithm is O(P(logQ) + Q(logR)).
Example:
A = [1, 5, 6]
B = [3, 7, 8]
C = [2, 4, 9]
First find the count of all j <= k such that B[j] ≤ C[k] and store it in an array.
t1 = [2,1,1]
convert it into postfix-sum array
t1_new = [4,2,1]
Now for every A[i] we need to find out the index of B[j](say x) which is just greater than A[i] and x >= i. The corresponding values would look like.
t2 = [1, 2, 3] (Array has 1-based indexing).
- The value just greater than 1 is 3(at index 1) in B[].
- The value just greater than 5 is 7(at index 2) in B[].
- The value just greater than 6 is 8(at index 3) in B[].
All the values greater than these indexes will be added in the final answer.(hence the postfix-sum array has to be maintained).
The final answer is:
ans = (t1[1]+t1[2]+t1[3])+(t1[2]+t1[3])+(t1[3]) = t1_new[0+1]+t1_new[1+1]+t1_new[1+1] = 4+2+1 = 7 ~~~~~
2-pointer search
2-pointer search just reduces the complexity of finding the index of C[k] which is just smaller than B[j] from O(n logn) to O(n). The approach is very intuitive and can be directly used to find the number of values which are larger than B[j] in C[k] such that j <= k directly.
Considering an example:
B = [1, 4, 5]
C = [2, 3, 6]
Let there be two pointers fixed at j=Q and k=R.
Move the pointers such that whenever:
1. B[j] ≤ C[k].
keep on decrementing k till B[j]>C[k]. The difference of R and present k (=R-k) is the number of values which are larger than B[j] in C[k] such that j <= k.
2. B[j] > C[k]
keep on decrementing j till B[j] ≤ C[k].
The same approach will be used to calculate i <= j <= k such that A[i] ≤ B[j] ≤ C[k] using a postfix sum array as described in method 1.
Complexity: O(P+Q+R)
Solution: http://goo.gl/N4qy6Z
Links: http://www.geeksforgeeks.org/find-a-triplet-that-sum-to-a-given-value/
http://leetcode.com/2010/04/finding-all-unique-triplets-that-sums.html
http://www.quora.com/Given-an-array-S-of-n-integers-are-there-elements-a-b-c-in-S-such-that-a-+-b-+-c-0-Find-all-unique-triplets-in-the-array-which-gives-the-sum-of-zero/answer/Raziman-Thottungal-Valapu
http://stackoverflow.com/questions/3815116/given-two-arrays-a-and-b-find-all-pairs-of-elements-a1-b1-such-that-a1-belong
http://www.geeksforgeeks.org/count-pairs-difference-equal-k/
-----------------------------------------------------------------------------------
100589K - Police Catching Thief
Basic Idea
Apply Multi-Source Dijkstra twice : First taking the K policemen's initial position as source and second taking the Q special nodes with power-ups, as source. This would get us the shortest time in which Police can reach any node in the graph in shortest time with or without using the power-up.
Apply a third Dijkstra using the initial position of Thief as source and just check if at any node the police can catch the thief (reach the node before or at equal time as thief) or not.
Note
The above approach works for a more general question when Vt and Vp need not be equal to 1 . Since in the above question Vt = Vp = 1 (to make the question simpler). For Thief , we can just check who reaches the final destination first, the police or thief because if the police can catch the thief on the way, it can definitely reach the destination before or at equal time as that of thief since Vp >= Vt always in this case.
(The proof of this is left to readers and also why it won’t work if Vp < Vt).
Explanation
There are many interesting things to note in this question. Lets analyze the question from the basics.
First , What does the question ask us to do? The Police needs to catch the thief. But the power-up makes the process interesting. Although it’s specifically mentioned that only single power-up is available for use, but the thief doesn’t know which policeman will avail which power up to increase his speed and we need to print the shortest time in which thief can escape regardless of whatever path the police might take. Therefore, when asked if the thief can escape or not, we can safely assume that the police will take the best possible combination of special node and power up to catch the thief. That is, for each node, we need to know the shortest time in which police can reach that node with or without taking the power up. This assumption doesn’t violate the fact that we have only a single power-up because suppose for some node “x”
reachingTimeOfPolice[x] <= reachingTimeOfThief[x]
Then, in such a case , the police can catch the thief at node x. This means that one of the K different Policemens can reach node ”x“ before the thief and can catch him there with or without using the power-up depending on the position of node x. Therefore, the thief cannot be sure of reaching his destination using this path because a single policeman using only a single power-up (or maybe even without it) can catch him.
Therefore, in short, we need to find the shortest time in which police (i.e any of the K different policemen) can reach any node (or only the destination in this case. See the NOTE) with or without using the power-up (whichever takes the shorter time). Once we have this information with us, we can simply check if the police reaches any node (or only the destination in this case) before thief and if this is the case, the thief cannot take that path. Like this, check for every node and just print the shortest time taken by the thief to reach the destination along such a path where no police can catch the thief at any node.
Second, How to do it?
A single multi-source Dijkstra taking the K different police-men’s initial positions as the source would give us the shortest time in which the police (i.e. any one of the K different policemen) can reach any node in the shortest time without taking the power-up. Next apply another multi-source Dijkstra using the Q different special nodes as source and this time, make sure to put :
startTimeOfSpecialNode[i] = policeTimeWithoutPowerUp[SpecialNode[i]];
After the second Dijkstra,
policeTime[i] = min(policeTimeWithoutPowerUp[i], policeTimeWithPowerUp[i]);
Next, apply a third Dijkstra for thief and add a condition that :
if(thiefTime[i]<policeTime[i])
Only Then explore its neighbours
else
thiefTime[i] = INF
The above condition is for the general case. For this specific question just check
if(thiefTime[Destination]<policeTime[Destination])
Print thiefTime[Destination]
else
print -1











There is a simpler o(N*sqrtN) solution for Queries on the tree using normal sqrt Decomposition of the euler array of the graph.
Yes, I realised the approach but couldn't write the editorial for it. It would be great if you explain it in few lines for others :).
You can perform one dfs and using Euler tour technique you can think of the tree as an array such that every sub-tree is a contiguous sequence in the array. Now split the array into blocks of sqrt(N) size, where N is the size of the array, and for each block store its total, and the number of nodes of any depth that it has.
To perform update simply increase the total of every block by the count of the number of nodes of the given depth it has.
To perform query, you need to return the sum of a sub-array. For all the blocks that lie entirely in the sub-array just add their total to your answer. For the rest of nodes, add them one-by-one.
much simpler approach. kudos man :)
Can you post your code somewhere?
http://ideone.com/YvK3tN
Count Palindromes : s = ab * 60 * 60 + cd * 60 + ef I got a penalty due to this.
In 'three sorted arrays' binary search solution : Is the value of t1=[2 1 0] correct? Also while calculating answer 'ans = t1[1]+t1[2]+t1[2] = 3+3+1' why are we doing this?
@shubham_466. The editorial has been updated. I hope it's clear now. Do reply if you have any query regarding this. :)
I have implemented what has been mentioned in the editorial but it is giving wrong answer on test case #6.
Solution Link http://ideone.com/SS4RAe
Where am I going wrong?
Dsets can be done in (logn * loglogn) at best right ? Or is there a better solution ?
Updated the editorial.
But there is no implementation written there. The complexity of my code was O(logn)^2 and it passed but I am not sure if it can be done faster (logn * (loglogn) ) is also possible but it doesn't look it will speed the code up by much.
My solution to 100589F - Count Ways is giving TLE on Test #2.
I have done exactly what is mentioned in the editorial. I calculate the
F()inO(logn). Am I supposed to calculate it inO(1). What am I doing wrong?Yes, you need to calculate all factorials and their inverses intially to reduce the complexity.
I did calculated the factorials before but I forgot about invfactorials.Silly me..Thanks got it Accepted :)
My submission for 'Count Ways' : 12217861
I could not understand the reason for getting WA on test-2. Could you please look into it once?
A very good problem set and well written editorials ! What more can one ask for? Great work!
For the Question-A Queries on trees.. i tried using sqrt-decomposition but yet i cant seem to pass the second test case.. it would be really helpful is someone could look at my code and point out my mistake http://ideone.com/4fE40H
Problem J — Really good one :) .. Missed AC in contest due to slow IO :/
And for problem "Count palindromes" , even precomputation can be simplified so as to include only the necessary 96 combinations.It can be done in O(24 * 6) time. 24 — For hours and seconds(since palindrome) while minutes can take only the values of 00,11,22,33,44,55(hence 6). Then we can simple iterate the 96 combinations and report answers :)
I amgetting wrong answer at testcase 2.I have used the method described above.Plz anyone help me.http://ideone.com/JMbt1a
What is 'r' in the pseudo code of problem H?
How is even F working ? I am not able to wrap my head around that F solution is working. is it inclusion-exclusion.It looks like the contribution of each black cellis subtacted from all cells which got added by it It looks like it works but yet difficult to believe it works