Lets discuss the solutions.
→ Pay attention
→ Streams
→ Top rated
| # | User | Rating |
|---|---|---|
| 1 | tourist | 3880 |
| 2 | jiangly | 3669 |
| 3 | ecnerwala | 3654 |
| 4 | Benq | 3627 |
| 5 | orzdevinwang | 3612 |
| 6 | Geothermal | 3569 |
| 6 | cnnfls_csy | 3569 |
| 8 | jqdai0815 | 3532 |
| 9 | Radewoosh | 3522 |
| 10 | gyh20 | 3447 |
→ Top contributors
| # | User | Contrib. |
|---|---|---|
| 1 | awoo | 161 |
| 2 | maomao90 | 160 |
| 3 | adamant | 156 |
| 4 | maroonrk | 153 |
| 5 | atcoder_official | 148 |
| 5 | -is-this-fft- | 148 |
| 5 | SecondThread | 148 |
| 8 | Petr | 147 |
| 9 | nor | 144 |
| 10 | TheScrasse | 142 |
→ Find user
→ Recent actions
↑
↓
Codeforces (c) Copyright 2010-2024 Mike Mirzayanov
The only programming contests Web 2.0 platform
Server time: Jul/27/2024 07:08:30 (f1).
Desktop version, switch to mobile version.
Supported by
User lists


| Name |
|---|











Interested in F, G, H, B, J
H:
If segment is short enough (r-l <= 1500), just check all the numbers from it. Otherwise, order(a) is small enough, check all ak.
To check if i = ak, you can calculate . Then i = ak if and only if y%x = 0.
. Then i = ak if and only if y%x = 0.
And what does order(a) denotes? (sorry for such a silly question)
order(a) — such minimal k, that ak = 1.
Well, looks like it's the same with order(a)%order(i) = 0 :)
And how to find order(a)? I mean, if r-l <= 1500 then order(a) is big right? So we can't find it in naive way?
We can do it in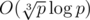 since
since 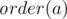 is always a divisor of
is always a divisor of 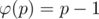 .
.
To check if i = ak it's enough to check that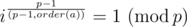 . So you need to calculate only order(a) once.
. So you need to calculate only order(a) once.
Wow, nice!
I wrote this contest resently. I don't know why this formula right.
I wrоte i ^ (order(a)) == 1 and it passed test.
And i ^ ((p — 1) / order(a)) don't work. WA34 [gcd(order(a), p — 1) = order(a)]
What am i miss?
G — find some corner square first. You can find one of it's corners as vertex with degree 2, two more corners as neighbours of this vertex, and last one as other common neighbour of vertices #2 and #3. Now do some sort of BFS — for every edge of a grid which you already have, let's say it is connecting vertices A and B, check if there exist such pair of yet unused vertices C, D, that there exist edges A-C, B-D, C-D. It will give you new square, and you can get exact position of C and D.
J: It is easy to show that the problem can be solved in O(m*2^k): iterate over all subsets of optional vertices and find MST of induced graph. Next, we generated multiple random graphs and found out that optimal subset always have <= 4 optional vertices. So our final solution is O(m*C(k, 4)).
Also, I believe I can solve F in with 2D structure, but it is so hard to implement :(
with 2D structure, but it is so hard to implement :(
F is pretty simple. Let's do the following iteration BUBEN number of times. For each group of points we define some random number. Now let's check the rectangles. If rectangle contains inside 2 * (sum all random numbers) we say it is good, otherwise — bad. If rectangle is good for all BUBEN iterations — it is good, otherwise — BAD. How to implement: scan line and simple Fenwick tree (add in point, range sum).
And what about fair solution?..
This is fair :) Try to find test to break it.
But isn't there solution without magic?
Probably, but this one has same amount of magic as hashes. I believe the idea is here. I would be interested to see if there is another solution of course. But I bet author wanted that one.
Actually, simple polynomial hash works fine.
I prefer the following version of about the same algorithm that it is much easier to prove. Let's denote digitwise sum modulo 4 as (like xor but in 4-ary numeral system, adding without carry). Assign each group a random number ri. Easily calculate such modified sum of all points inside each rectangle by using scanline and 1d data structure. Then if the result in rectangle is actually
(like xor but in 4-ary numeral system, adding without carry). Assign each group a random number ri. Easily calculate such modified sum of all points inside each rectangle by using scanline and 1d data structure. Then if the result in rectangle is actually 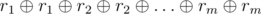 then this rectangle is good, otherwise it's not.
then this rectangle is good, otherwise it's not.
How to prove correctness. It is easy to see that there is no false-negative results, only false-positive. It is easy to show that if rectangle isn't actually good (i. e. there is at least one group of points that has 0, 1, 3 or 4 points in intersection with it), than the single digit of a result will be equal to a corresponding digit of expression above with probability exactly 1 / 4. So, if we take the 30-digit 4-ary number (a single long long), then the probability of false positive result is 1 / 430 that can be discarded as impossible.
It's not magic, it's probabilistic algorithm.
Let all random numbers are 32-bit. Then BUBEN = 1.
Apparently, we have forgotten to switch BUBEN from 1 to 30 :) We had a bug and when stressed, switched it to 1. Then found it we just submitted and got OK. With BUBEN = 30 we had TLE 49.
I am sorry for stupid question but how we build 2d fenvic tree with coordinates range from -10^9 to 10^9?
How to solve D?
D: First do a binary search on answer, that is width. Then DP. I did DP in two steps. First precomputation and then construction. In precomputation step, DP parameter was: DP[i][j] which means: how many of log2 is required if I use j number of log1 to construct 2^i rows in total. Using, O(n^2) loop, you can construct: DP[1], DP[2] and so on.
Then you can find out your answer using binary representation of L (and corresponding DP[] array).
Let's do binary search by the answer.
Let's say we have fixed answer M and we want to check if we can achieve it. This task is solvable using dynamic programming. Let r(x,p) denote the smallest number of sticks of the second type, that we need to build exactly l blocks of size M or bigger. We will iterate through all possible number of sticks of the first type and do our transitions. Such solution works in O(n^3logN) time per test case and surprisingly passes the TL.
There exists a cool optimization, which makes our code to work in O(N^2logN) time. Let's calculate, how many iterations will our DP make in all states. This number is equal to x*l*((x*a+y*b)/l)/a. L = ((x*a+y*b)/l) is the maximum size of our block, an we will make no more then L/a iterations in each state. It's easy to show, that x*l*((x*a+y*b)/l)/a = x*x+x*y*b/a. Now let's do our trick. If b is bigger then a — let's swap them, and it's easy to see, that our DP will work in O(N^2) time in this case
For fixed binared width: dp[c1][c2] — using c1 first type, c2 second, what is maximum pair (finished rows count, remaining in last not finished row)
Why do we store "remaining in last not finished row"? Does it help with transitions?
It help in calculating next dp in 2 variants: If remaining + a >= width so new c1 = c1 + 1, new remaining = 0, and we have one more finished row. If remaining + a < width only c1 = c1 + 1 and remaining += a
Maybe I misunderstood you, but I got WA2 with this code: Link
Solution
Binary search on the answer reduces this problem to answering whether the point (x, y) lies outside or on the border of the Minkowski sum of l copies of the convex (more like "concave" in this case) hull of the polygon formed by the points (px, py) such that apx + bpy ≥ tentative_answer and this sum is homothetic to the polygon itself. The complexity is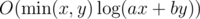 per testcase.
per testcase.
Sorry did not get it, code?
This should work: http://pastie.org/10101937
How to solve J Div2 (k <= 10)?
My solution was: minimum spanning tree for each bitmask of last k vertices that we will remove from graph.
Found mistakes: 1) Check if what we got from Kruskal is actually tree, 2) if (k >= n-1) print "0".
I forgot to mention, that it's WA21.
Best solution for E:
Statistics of this approach:
Here,
x+y / zmeans there werezOKs,xteams used this approach, andymore teams tried this after accepting a normal solution.That's definitely an improvement comparing to my previous attempt to put an Easter Egg into an ACM-style problem, where only one team passed one test using it.
Kudos to the people who got it!
How to solve K?
You should twice apply the operator and you will have 3 vectors and 3 points that defines a plane. Normal — is the axis. Angle you can find between vectors (from center of circle to two neighbor points on circle) Circle in this plane.
B?
In B we had the following solution. First with FFT we calculated all deltas we have, so for each delta [0..400000] we can tell if there are xi and xj that xj — xi == delta. Now we need to find these xi and xj for each delta. We randomly generated i, j and marked the delta as found. Then we just found all other deltas (not found) naively. That is hacky but got AC. Interested in the other solutions.
Ok, my fault, got the idea.
One FFT convolution (and 3 FFTs).
more details may be?
O(C2) solution, where C -- maximal time in input, using bitset optimisation, worked in 0.35 seconds.
Could you describe it in more detail, please?
Let's for every difference d find two indices i and j, such that t[i] - t[j] = d.
We will maintain the bitset of the values of differences, which we didn't find answer for. Let's iterate over t[j] in ascending order, and do "bitwise and" for that bitset and the bitset which contains all t[i] - t[j]. If there are elements, then in 32 or 64 operations learn which bit, and update the answer for all of them.
My author solution has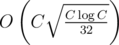 complexity: I used FFT + SQRT decompostion + BitMasks. I've tried to make tests agains many "hacky" solutions, but it seems, that i've failed=(
complexity: I used FFT + SQRT decompostion + BitMasks. I've tried to make tests agains many "hacky" solutions, but it seems, that i've failed=(
This solution got AC in upsolving.
This task is about finding such a pair of people for every difference (it can take values between 0 and 400000) that t[j] — t[i] equals this difference if there is any. Let's fix a constant K, consider a time interval 0..400000 divided into blocks of length K.
Each block we represent as bitmask (K is small enough to fit in int), where 1 means there is a person to come in this time. Next, for all pairs of blocks we precalculate array p[mask1][mask2] — a mask of differences between the first and the second blocks, which can be obtained if we concatenate blocks (it can be easily done in O(2 ^ (2 * K)) time and memory). Note that if we can find a block for given difference which contains the first element of a pair, which gives this difference, we can establish the pair in O(K). Now we iterate over all pairs of blocks, in O(1) find a mask of differences for this pair (using p for this), and try to update the answer for each found difference. To do it fast, we need firstly to iterate over all pairs with equal distances between first and second blocks. For small differences (< K) use brute force.
Complexity: O((N/K) ^ 2) + O(2 ^ (2 * K)) time and O(2 ^ (2 * K)) memory. I chose K = 12.
when upsolving will be open?
It is open in yandex contest from the end of the contest
Where can I read the fkin problems? Why the link to the problemset is absent on opencup.ru? Why opencup becomes more and more private?
Div 1
Div 2
Hello)) Did you faced with the problem in task "List powers" TL or memory limit on 36 test or TL on 41 test? http://pastebin.com/tPNBtdAt this is code with memory limit on 36th test... How I can fix it?
You can speed up both parts of your solution.
For
solve_interval, you can check the orders of elements instead of finding the discrete logarithm (see this thread for details).For
solve_powers, you can get rid of the unordered map and just iterate until you get 1.Either of these changes will perhaps be sufficient.
Thank you))