Arterm's blog

Good Code
By Arterm, 9 years ago, In English

Good day everyone.

Every programmer occasionally, when nobody's home, turns off the lights, pours a glass of scotch, puts on some light German electronica, and opens up a file on their computer. It's a different file for every programmer. Sometimes they wrote it, sometimes they found it and knew they had to save it. They read over the lines, and weep at their beauty, then the tears turn bitter as they remember the rest of the files and the inevitable collapse of all that is good and true in the world.
This file is Good Code. It has sensible and consistent names for functions and variables. It's concise. It doesn't do anything obviously stupid. It has never had to live in the wild, or answer to a sales team. It does exactly one, mundane, specific thing, and it does it well. It was written by a single person, and never touched by another. It reads like poetry written by someone over thirty.

(excerpt from http://www.stilldrinking.org/programming-sucks)

Do you have such code? For me it's code for binary power

long bin(long x, long a) {
   long y = 1;
   while (a) {
      if (a & 1)
         y = (y * x) % mod;
      x = (x * x) % mod;
      a >>= 1;
   }
   return y;
}

and Gauss algorithms (the latter is longer than nine lines, so I don't post it here).

I'll be happy to see yours masterpieces!

  • Vote: I like it
  • +145
  • Vote: I do not like it

Comments Comments (126)
| Write comment?
»
9 years ago, # |
  Vote: I like it +5 Vote: I do not like it

Quicksort in Haskell:

quicksort [] = []
quicksort (p:xs) = quicksort (filter (<= p) xs) ++ [p] ++ quicksort (filter (> p) xs)
→ Reply
»
9 years ago, # |
← Rev. 2   Vote: I like it +120 Vote: I do not like it

It has sensible and consistent names for functions and variables.

long bin(long x, long a) {
   long y = 1;
   ...

Names are consistent for sure.

→ Reply
»
9 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Fast exponentiation would be one of my first choices as well along with several other pieces of code that rely on bit masks, specially DP with bit masks, for example storing all ancestors of a node of a tree that are 1 << i distant from it and then using those values to calculate lca of two nodes: That's what I call perfection, the way it all fits together.

That said since we are choosing a piece of code I would like to post the code to calculate the z function:

        public int[] functionZ(char[] str, int n) {
		int[] z = new int[n];

		int l = 0;
		int r = 0;
		z[0] = n;

		for (int i = 1; i < n; i++) {
			z[i] = Math.min(z[i - l], r - i + 1);

			while (i + z[i] < n) {
				if (str[z[i]] != str[i + z[i]]) {
					break;
				}
				z[i]++;
			}

			if (i + z[i] - 1 > r) {
				l = i;
				r = i + z[i] - 1;
			}

			r = Math.max(r, i);
		}

		return z;
	}

So fast, so beautiful and so powerful!

→ Reply
»
9 years ago, # |
← Rev. 2   Vote: I like it +18 Vote: I do not like it

Though a one-liner, my favorite is the recursive implementation of Euclid's Algorithm (GCD):

int gcd(int a, int b) {
  return a ? gcd(b % a, a) : b;
}
→ Reply
  • »
    »
    9 years ago, # ^ |
      Vote: I like it +11 Vote: I do not like it

    Not recursive version

    int gcd( int x, int y )
{
  while (x&&y) x>y ? x%=y : y%=x;
  return x+y;
}
    → Reply
  • »
    »
    9 years ago, # ^ |
      Vote: I like it +9 Vote: I do not like it

    what about this __gcd(a,b)

    → Reply
  • »
    »
    9 years ago, # ^ |
      Vote: I like it -10 Vote: I do not like it

    Personally I prefer this :

    int gcd(int a,int b)
{
    if(a && b)
        while(a%=b^=a^=b^=a);
    return a+b;
}
    → Reply
»
9 years ago, # |
  Vote: I like it -7 Vote: I do not like it

gcd in python, is my favourite (from fractions module, not mine) 

def gcd(a, b):
    while b:
        a, b = b, a % b
    return a
→ Reply
»
9 years ago, # |
  Vote: I like it +10 Vote: I do not like it

I like my implementations of string algorithms. For example, KMP:

int pi[100000];

void build_pi (string& str)
{
    int k = pi[0] = -1;
    
    for (int i = 0; i < str.size(); ++i)
    {
        for (; k >= 0 && str[i] != str[k]; k = pi[k]);
        
        pi[i + 1] = ++k;
    }
}

void kmp_match (string& p, string& text)
{
    build_pi(p);
    
    for (int i = 0, k = 0; i < text.size(); ++i)
    {
        for (; k >= 0 && text[i] != p[k]; k = pi[k]);
        
        if (++k == p.size())
            cout << "match at: " << i - p.size() + 1 << endl;
    }
}
→ Reply
  • »
    »
    9 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    Does the build_pi() function work properly for strings like "aba" or "abcde"?

    → Reply
    • »
      »
      »
      9 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      Let's see. pi[i] is equal to the length of the border of the string compound by the first i characters of str.

      The output for "aba" is:

      -1 0 0 1

      and for "abcde" is:

      -1 0 0 0 0 0

      So I think that yes, it works properly.

      → Reply
      • »
        »
        »
        »
        9 years ago, # ^ |
          Vote: I like it 0 Vote: I do not like it

        My bad, I didn't notice your pi[] array uses 1-based indexing. Sorry for that.

        → Reply
  • »
    »
    9 years ago, # ^ |
      Vote: I like it -11 Vote: I do not like it

    You may consider using ~k instead of k >= 0.

    → Reply
    • »
      »
      »
      9 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      I don't understand what do you mean?

      → Reply
      • »
        »
        »
        »
        9 years ago, # ^ |
        ← Rev. 4   Vote: I like it +2 Vote: I do not like it

        ~k is a way to check if k is -1 or not. In the following code, the print statement won't be executed.

        int k = -1;
if (~k) printf ("Hello World\n");

        In your code, as you are checking if k is -1 or greater (umm, that's what I think :D), so you may replace k >= 0 with ~k if you want.

        (explanation: -1 contains all ones in its bit representation. So it's compliment ~(-1) contains all zeros i.e. 0. For every other numbers, they contain atleast one zero in their bit representation. So their compliment contains atleast one 1, i.e. non-zero)

        → Reply
        • »
          »
          »
          »
          »
          9 years ago, # ^ |
            Vote: I like it +8 Vote: I do not like it

          Yes, you are right. I got it now. Although I think that maybe this trick is too dark in this case ;)

          → Reply
          • »
            »
            »
            »
            »
            »
            9 years ago, # ^ |
              Vote: I like it 0 Vote: I do not like it

            Actually I use it pretty much everywhere (reading till EOF, traversing edge-list, custom stacks etc) :p

            → Reply
  • »
    »
    9 years ago, # ^ |
      Vote: I like it +5 Vote: I do not like it

    By the way, you don't have to do the matching separately. You can create a string X = pattern + SEPARATOR + text, build the pi array for X and check which indices have pi[index] = pattern.size() :).

    → Reply
»
9 years ago, # |
  Vote: I like it +8 Vote: I do not like it

I like my segment tree!

node seg[2 * N]; // N is some power of two

void add(int i, node x)
{
	seg[i += N] = x;
	for(i /= 2; i; i /= 2)
		seg[i] = merge(seg[i * 2], seg[i * 2 + 1]);
}

node get(int l, int r)
{
	node resL, resR;
	for(l += N, r += N; l < r; l /= 2, r /= 2)
	{
		if(l % 2)
			resL = merge(resL, seg[l++]);
		if(r % 2)
			resR = merge(seg[--r], resR);
	}
	return merge(resL, resR);
}
→ Reply
»
9 years ago, # |
  Vote: I like it +162 Vote: I do not like it

Computing Euler's totient function for all natural numbers <= n in O(n*log n):

int[] phi = new int[n + 1];
for (int i = 1; i <= n; ++i) {
  phi[i] += i;
  for (int j = 2 * i; j <= n; j += i) {
    phi[j] -= phi[i];
  }
}
→ Reply
  • »
    »
    9 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    Do you know some problems on Codeforces that are solvable using this function ?

    → Reply
  • »
    »
    9 years ago, # ^ |
      Vote: I like it +11 Vote: I do not like it

    You can make it +-4x faster (though not quite as elegant):

    int *phi = new int[n + 1];
for (int i = n; i > 0; i--) {
    phi[i] = i;
}
for (int i = 2; i <= n; i++) {
    if (phi[i] == i) {
        for (int j = i; j <= n; j += i) {
            phi[j] = phi[j] / i * (i - 1);
        }
    }
}
    → Reply
  • »
    »
    9 years ago, # ^ |
    ← Rev. 3   Vote: I like it +7 Vote: I do not like it

    Thank you winger, this is really elegant code. And cost me long time to think:


    Maybe my understanding will help other people: 

1. From the code, we know that the code is valid iff: 
                  sum{phi[d] |  n % d== 0} == n

   For example: phi(1)+phi(2)+phi(3)+phi(4)+phi(6)+phi(12)=1+1+2+2+2+4=12
2. How to prove? 
   I do not know how to prove, then I found an excellent proof here: 
   http://2000clicks.com/mathhelp/NumberFactorsTotientFunction.aspx
    → Reply
  • »
    »
    9 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    You forgot to do Phi[i]--; after it has been used because totient of prime number n is n-1

    → Reply
    • »
      »
      »
      9 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      The first iteration (with i=1) does exactly that.

      → Reply
  • »
    »
    9 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    Will calculation using Eratosthenes sieve be faster? Seems that it has better complexity O(n loglog n)

    → Reply
»
9 years ago, # |
  Vote: I like it +1 Vote: I do not like it

Sparse Table Data Structure (masterpiece)

int arr[MAXN];
int mx[MAXN][LOGN];
void init() {
    for (int i = 0; i < n; i++)
        mx[i][0] = arr[i];
    for (int j = 1; (1 << j) <= n; j++)
        for (int i = 0; i + (1 << j) - 1 < n; i++)
	    mx[i][j] = max(mx[i][j - 1], mx[i + (1 << (j - 1))][j - 1]);
}
→ Reply
»
9 years ago, # |
  Vote: I like it +157 Vote: I do not like it

Floyd-Warshall algorithm

for(int k = 0; k < n; k++)
  for(int i = 0; i < n; i++)
    for(int j = 0; j < n; j++)
      d[i][j] = min(d[i][j], d[i][k] + d[k][j]);
→ Reply
»
9 years ago, # |
← Rev. 2   Vote: I like it +42 Vote: I do not like it

Computing Modular Inverses (Modulo a Prime) for Natural Numbers <= N:

inv[1] = 1;
for (int i = 2; i < N; i++) { inv[i] = (MOD - (MOD / i) * inv[MOD % i] % MOD) % MOD; }
→ Reply
  • »
    »
    9 years ago, # ^ |
      Vote: I like it +4 Vote: I do not like it

    This works with primes only.

    If MOD=12, inv[5] relies on inv[2], which is not specified.

    → Reply
    • »
      »
      »
      9 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      Fixed, thanks. It's been too long since I've worked with MOD != 1000000007 :)

      → Reply
»
9 years ago, # |
  Vote: I like it +67 Vote: I do not like it

A one-liner to calculate modular inverse, returns 0 if gcd(a,m) != 1.

int inv(int a, int m) {
 return a < 2 ? a : ((1 - m * 1ll * inv(m % a, a)) / a % m + m) % m;
}
→ Reply
»
9 years ago, # |
  Vote: I like it +29 Vote: I do not like it

Path compression!

On a related note, how do I add codes in comments, with proper formatting?

→ Reply
  • »
    »
    9 years ago, # ^ |
      Vote: I like it +5 Vote: I do not like it

    Click on the second last option on the menu bar, and then click on Block. Put your code inside the tildes generated.

    → Reply
  • »
    »
    9 years ago, # ^ |
      Vote: I like it +39 Vote: I do not like it

    I prefer less readable

    int root(int v) {
    return dad[v] = dad[v] == v ? v : root(dad[v]);
}
    → Reply
  • »
    »
    9 years ago, # ^ |
      Vote: I like it +11 Vote: I do not like it 
    int t[MXN];
int Find(int x)
 {
 return x == t[x] ? x : t[x] = Find(t[x]);
 }
void Union(int x,int y)
 {
 t[Find(x)] = y;
 }

    :)

    → Reply
»
9 years ago, # |
  Vote: I like it -26 Vote: I do not like it

The power of Python.

def isPalindrome(s):
  if s == s[::-1]:
    return True
  return False

a, b = b, a   #Swapping
→ Reply
  • »
    »
    9 years ago, # ^ |
      Vote: I like it +79 Vote: I do not like it 
    def isPalindrome(s):
 return s == s[::-1]

    :|

    → Reply
  • »
    »
    9 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    The power of C++.

    bool isPalindrome(string s, string t = "") {
	return reverse_copy(s.begin(), s.end(), back_inserter(t)), t == s;
}

int main() {
	string s;
	cin >> s;
	cout << isPalindrome(s);
}
    → Reply
    • »
      »
      »
      9 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      or just

      bool is_pal(string&& s) { 
  return string(s.rbegin(), s.rend()) == s;
}
      → Reply
      • »
        »
        »
        »
        9 years ago, # ^ |
          Vote: I like it +39 Vote: I do not like it

        No need to create a new string:

        inline bool is_palindrome(const string& s)
{
    return std::equal(s.begin(), s.end(), s.rbegin());
}
        → Reply
»
9 years ago, # |
  Vote: I like it +55 Vote: I do not like it

Bogosort.

vector<int> bogosort(vector<int> A) {
    while(!is_sorted(begin(A),end(A))) random_shuffle(begin(A),end(A));
    return A;}
→ Reply
»
9 years ago, # |
  Vote: I like it +18 Vote: I do not like it

Maximum flow. (Can the code be made better?)

int maxFlow(int[][] cap, int source, int sink) {
  for (int flow = 0; ; ++flow)
    if (!augmentPath(cap, new boolean[cap.length], source, sink))
      return flow;
}

boolean augmentPath(int[][] cap, boolean[] vis, int i, int sink) {
  if (i == sink) return true;
  vis[i] = true;
  for (int j = 0; j < vis.length; j++)
    if (!vis[j] && cap[i][j] > 0 && augmentPath(cap, vis, j, sink)) {
      --cap[i][j];
      ++cap[j][i];
      return true;
    }
  return false;
}
→ Reply
  • »
    »
    9 years ago, # ^ |
      Vote: I like it +26 Vote: I do not like it

    maybe only asymptotically

    → Reply
  • »
    »
    9 years ago, # ^ |
      Vote: I like it +8 Vote: I do not like it

    This one is a bit longer but faster than most of the implementations I've seen. (My template and a sample implementation)

    int __dfs__ (int u, int F) {
    if (u == t) return F;

    for (int i = head [u]; ~i; i = from [i]) {
        int v = to [i];
        if (c [i] - f [i] > 0 && h [v] + 1 == h [u]) {
            int flow = __dfs__ (v, min (F, c [i] - f [i]));
            f [i]     += flow;
            f [i ^ 1] -= flow;
            if (flow > 0) return flow;
        }
    }

    if (--gap [h [u]] == 0) h [s] = N;
    ++gap [++h [u]];
    return 0;
}

int flow () {
    int ret = 0; gap [0] = N;
    while (h [s] < N) ret += __dfs__ (s, INF);
    return ret;
}
    → Reply
»
9 years ago, # |
  Vote: I like it +17 Vote: I do not like it

Two pointers:

for (int L = 0, R = 0; L < n; L++) {
    while (R < n && !someCondition(R)) R++;
    updateSomething(L, R);
}
→ Reply
»
9 years ago, # |
← Rev. 2   Vote: I like it +33 Vote: I do not like it

Binary search without overflow:

// 000[1]11
int binarySearchFirstTrueValue(IntPredicate predicate, int fromInclusive, int toExclusive) {
  int lo = fromInclusive;
  int hi = toExclusive;
  while (lo < hi) {
    int mid = (lo & hi) + ((lo ^ hi) >> 1);
    if (!predicate.test(mid))
      lo = mid + 1;
    else
      hi = mid;
  }
  return hi;
}
→ Reply
  • »
    »
    9 years ago, # ^ |
      Vote: I like it +4 Vote: I do not like it

    omg xD, so useful, much trick

    If you like such nasty bits tricks take a look here: http://codeforces.com/blog/entry/13410#comment-182868

    → Reply
    • »
      »
      »
      9 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      It seems that the trick with int mid = (lo & hi) + ((lo ^ hi) >> 1); is necessary evil here. Can't invent how to correctly calc mid in a more simple way.

      → Reply
      • »
        »
        »
        »
        9 years ago, # ^ |
        ← Rev. 2   Vote: I like it 0 Vote: I do not like it

        I guess that you disregard (lo + hi) / 2 since you emphsized that this binary search is "without overflow", but can you give me a link to at least one problem, when you needed to handle numbers bigger than 263, so adding such numbers will cause overflow, even when using unsigned long long? I guess no, and even if there are such problems I think that lo / 2 + hi / 2 + (lo&hi&1) is simpler.

        → Reply
        • »
          »
          »
          »
          »
          9 years ago, # ^ |
            Vote: I like it +5 Vote: I do not like it

          lo / 2 + hi / 2 + (lo&hi&1) doesn't work for negative values. If lo=-3, hi=-1, result is 0 (instead of -2).

          → Reply
          • »
            »
            »
            »
            »
            »
            9 years ago, # ^ |
            ← Rev. 2   Vote: I like it +8 Vote: I do not like it

            Ehhhh... Playing with bits of negative numbers is something like dancing on the edge of canyon. That whole discussion is so utterly nonsense. Is this a REAL problem? If problemsetter is such an asshole that two times range overflows unsigned long long then he could as well demand bignums >_>.

            Taking care about not doubling the range is something extremely not important in my opinion, I would be more interested in not doubling the EXPONENT of range in geometry.

            → Reply
            • »
              »
              »
              »
              »
              »
              »
              9 years ago, # ^ |
                Vote: I like it +13 Vote: I do not like it

              The discussion turned out to be unfair because I initially thought about library implementation of binary search (which must work correctly for any legal input).

              I agree that solving a contest problem it is usually enough to merely use 64-bit integer if there is a risk of overflow.

              → Reply
      • »
        »
        »
        »
        9 years ago, # ^ |
          Vote: I like it +21 Vote: I do not like it

        I've always thought mid = lo + (hi - lo) / 2 does the thing. What's the downside of such operation?

        → Reply
  • »
    »
    9 years ago, # ^ |
    ← Rev. 2   Vote: I like it +21 Vote: I do not like it

    I use this approach instead:

    while (lo < hi-1) {
    int mid = (lo+hi)/2;
    if (!predicate.test(mid))
        lo = mid;
    else
        hi = mid;
}
return hi;

    Overflow stuff: it's usually better to use long longs where appropriate (with rules like "a computation that uses long longs doesn't return int"), not initialise anything to too big constants and not bother with details.

    → Reply
»
9 years ago, # |
  Vote: I like it +3 Vote: I do not like it

Take a Look at his codes -> Archon.JK

→ Reply
»
9 years ago, # |
← Rev. 2   Vote: I like it -6 Vote: I do not like it

Seeing many binary searches here I will put mine, which is in my opinion much more clear and safe. Everybody knows that binary search is extremely prone to mistakes, especially for beginners, so here's my completely invulnerable to any mistakes approach.

int kl = 1, kp = 1e9, res = 0;
while (kl <= kp) {
  int cur = (kl + kp) / 2;
  if (Test(cur)) {
    res = cur;
    kl = cur + 1;
  } else {
    kp = cur - 1;
  }
}
return res;

What's so special?

First reason: I keep an invariant that interval [kl, kp] is something I don't know anything about. Stop condition is obvious — that interval is nonempty <=> (kl <= kp). Many people try to keep an invariant as sth like "I know that first element of my interval is good, about others I don't know" or "I know that first element is good, last is bad, rest unknown", but in my opinon this is much more complicated to maintain and demand much more thought about when to end this (look at this lo < hi - 1 in Xellos' code :<). Another kind of problems it omits are all about initialization, it may be also troublesome to those solutions with invariants other than mine.

Second reason: It's invulnerable to any bugs like "if beginning is odd, end is even and checked value is not good, then blah, blah and I will end up in infinite loop" or "if beginning is negative, end is positive, then stupid division of negative numbers will cause rounding in bad side, so blahblah, infinite loop". I got those +1 and -1 in case of success or failure, so my search interval is clearly strictly shrinking, no matter what, being even/odd/positive/negative is of no relevance.

→ Reply
  • »
    »
    9 years ago, # ^ |
    ← Rev. 2   Vote: I like it +44 Vote: I do not like it

    omg, and you say it's easier to maintain then f(l) = true, f(r) = false ?

    And am I right that you have to carefully choose res for the case where test is never returns true?

    → Reply
    • »
      »
      »
      9 years ago, # ^ |
      ← Rev. 2   Vote: I like it 0 Vote: I do not like it

      OK, I agree that maintaining f(l) = true, f(r) = false is equally easy (don't tell me that's my way is not easy), HOWEVER... How do you initialize your boundaries so that f(l) = true and f(r) = false? Another advantage is that kl <= (kl + kp) / 2 <= kp, no matter what, so I always check something that I have not checked so far. If my invariant was f(l) = true, f(r) = false, then what I have to be sure is that (l + r) / 2 lies inside [l+1, r-1] interval. That may also be true, but surely it demands a long thought about all possible parities, about positivity/negativity and about careful stop conditions. I don't have any of those problems.

      In case when test never returns true I have res = -1 (or any other value not inside a starting interval), so it's trivial to handle this. In both indy's and Xellos' binary searches it is impossible to tell cases when test never returns true and if smallest value that test returns true is largest value in interval. However, indy handled it well since he named that largest value "toExclusive" (and probably Xellos handles it well also, but it can't be seen in that piece of code), but that's another thing to take care about, to remember that this value must be larger, in Xellos code that's at least nice symmetry, indy used "closed-open" concept which I personally hate and it makes it completely nonsymetrically between cases.

      → Reply
      • »
        »
        »
        »
        9 years ago, # ^ |
        ← Rev. 2   Vote: I like it +8 Vote: I do not like it

        Well, (l+r)/2 is always inside a range in my code too(if I haven't finished)

        Yes, sometimes it may be a bit tricky to get correct l,r if you do it for first time, but in general I would say, if you know how to write if for your -1, then you know how to write correct start condition

        → Reply
      • »
        »
        »
        »
        9 years ago, # ^ |
          Vote: I like it +8 Vote: I do not like it

        In contest problems I use the following symmetric version:

        int binarySearchFirstTrue(IntPredicate predicate, int fromInclusive, int toInclusive) {
  int lo = fromInclusive - 1;
  int hi = toInclusive + 1;
  while (hi - lo > 1) {
    int mid = (lo + hi) / 2;
    if (!predicate.test(mid))
      lo = mid;
    else
      hi = mid;
  }
  return hi;
}

        It is not obvious to check for correctness, but at least this version is highly symmetric and is similar to binary search in real domain:

        double binarySearchFirstTrue(DoublePredicate predicate, double lo, double hi) {
  for (int iteration = 0; iteration < 1000; iteration++) {
    double mid = (lo + hi) / 2;
    if (!predicate.test(mid))
      lo = mid;
    else
      hi = mid;
  }
  return hi;
}
        → Reply
  • »
    »
    9 years ago, # ^ |
    ← Rev. 2   Vote: I like it +3 Vote: I do not like it

    Then look at this kl = cur + 1 and kp = cur - 1 in Swistakk's code (two more +-1s) :D

    Whatever, man. As long as one doesn't mix up the boundaries of the interval, the rest is clear and easy to understand. It's just binary search, mistakes there are for noobs.

    I should dig out my FFT and put it here — master trole.

    → Reply
  • »
    »
    9 years ago, # ^ |
      Vote: I like it +13 Vote: I do not like it

    I don't understand why you get some downvotes. This is also EXACTLY how I always code binary search, and I also believe that this is the most intuitive way.

    Whenever I see someone write left = mid or right = mid, I am confused as how to make sure that this thing terminate correctly. It's even worse when people avoid creating new variable res and return left or right at the end. I don't understand why people spend extra time to deal with all these complications to make it work, while it could be so simple & beautiful.

    → Reply
»
9 years ago, # |
  Vote: I like it +18 Vote: I do not like it

Convex hull in O(n*log(n)) in Python:

# how to use: convex_hull([(0, 0),(2, 0),(0, 2),(2, 2),(1, 1)])
def convex_hull(points):
    def remove_middle(a, b, c):
        cross = (a[0] - b[0]) * (c[1] - b[1]) - (a[1] - b[1]) * (c[0] - b[0])
        dot = (a[0] - b[0]) * (c[0] - b[0]) + (a[1] - b[1]) * (c[1] - b[1])
        return cross < 0 or cross == 0 and dot <= 0

    hull = []

    for p in sorted(points) + sorted(points, reverse=True):
        while len(hull) >= 2 and remove_middle(hull[-2], hull[-1], p):
            hull.pop()
        hull.append(p)

    return hull[:-1]
→ Reply
»
9 years ago, # |
  Vote: I like it +28 Vote: I do not like it

calculate n-th Fibonacchi number (possibly modulo something) in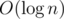 

pair<ll, ll> fib1(ll n) {
  if (n == 0) return {0, 1};
  auto cur = fib1(n / 2);
  ll b = cur.first;      
  ll c = cur.second;     
  ll a = c - b;          
  ll F1 = c * c - a * a;  
  ll F2 = c * c + b * b;  
  if (n % 2) return {F2, F1 + F2};
  return {F1, F2};
}

ll fib(ll n) { return fib1(n).first; }
→ Reply
  • »
    »
    9 years ago, # ^ |
    ← Rev. 2   Vote: I like it 0 Vote: I do not like it 
    i think this one is better : 

map<long long, long long> F;
long long fib(long long n) {
	if (F.count(n))
		return F[n];
	long long k = n / 2;
	if (n % 2 == 0) { 
		return F[n] = (fib(k) * fib(k) + fib(k - 1) * fib(k - 1)) % m;
	} else { 
		return F[n] = (fib(k) * fib(k + 1) + fib(k - 1) * fib(k)) % m;
	}
}
    → Reply
»
9 years ago, # |
  Vote: I like it +9 Vote: I do not like it

Reading single integer from input:

int n;
cin >> n;
→ Reply
»
9 years ago, # |
  Vote: I like it +31 Vote: I do not like it

Recursive Fenwick-Tree masterpiece [Please read the sentence with a proper British accent!]

int fen[N];

int get(int idx) {
	return idx > 0? fen[idx] + get(idx - (idx & -idx)): 0;
}

int upd(int idx, int v) {
	return idx < N? fen[idx] += v, upd(idx + (idx & -idx), v): 0;
}
→ Reply
»
9 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Z- and prefix- functions, maybe :)

    int p[n];
    p[0] = 0;
    for(int i = 1; i < n; i++)
    {
        p[i] = p[i - 1];
        while(s[i] != s[p[i]]) p[i] = p[p[i] - 1];
        if(s[i] == s[p[i]]) p[i]++;
    }
/*----------------*/
    int z[n];
    int l = 0, r = 0;
    for(int i = 1; i < n; i++)
    {
        z[i] = max(0, min(z[i - l], r - i));
        while(i + z[i] < n && s[z[i]] == s[i + z[i]]) z[i]++;
        if(i + z[i] > r) l = i, r = i + z[i];
    }
→ Reply
»
9 years ago, # |
← Rev. 8   Vote: I like it 0 Vote: I do not like it

Some short code

bool isPowerOfTwo(int n)
{
     return !(n & (n - 1));
}
void swap(int& a, int& b)
{
     a=a+b-(b=a);
}

in Java

public static boolean isPrime(int n) 
{
    return !new String(new char[n]).matches(".?|(..+?)\\1+");
}
→ Reply
  • »
    »
    9 years ago, # ^ |
      Vote: I like it +24 Vote: I do not like it

    It seems that second example is undefined behavior, because (as far as I understand) order of evaluation of a + b and (b = a) is not specified.

    → Reply
  • »
    »
    9 years ago, # ^ |
      Vote: I like it -14 Vote: I do not like it

    the swap function can be like this:

    a ^= b ^= a ^= b;
    → Reply
»
9 years ago, # |
← Rev. 3   Vote: I like it +22 Vote: I do not like it 
int days(int y, int m, int d)
{ // number of days from 1 january 0 (1-indexed)
	if (m < 2) y--, m += 12;
	return 365 * y + y / 4 - y / 100 + y / 400 + (153 * m + 1) / 5 + d - (y == -1);
}

for (int mask = (1 << k) - 1; mask < (1 << n); )
{ // all masks with n bits and k ones, add yout code before if
	if (mask == 0) break;
	int x = mask & -mask, y = mask + x;
	mask = (((mask & ~y) / x) >> 1) | y;
}
→ Reply
»
9 years ago, # |
← Rev. 4   Vote: I like it +5 Vote: I do not like it

Computing inverse modulo MOD for all natural numbers < MOD in O(n):

void GetAllInverseElements(int mod){
  ll inv[mod]; inv[1] = 1;
  for (int i=2; i<mod; i++){
    inv[i]= (mod/i) * inv[mod % i];
    inv[i]= (mod - inv[i] %mod)% mod;
  }
}
→ Reply
»
9 years ago, # |
  Vote: I like it +8 Vote: I do not like it

My favourite is implicit cartesian tree: http://pastebin.com/8fhVg3r4

→ Reply
»
9 years ago, # |
  Vote: I like it +5 Vote: I do not like it

I like many many many algorithms and functions. One that comes to mind now is inclusion-exclusion principle, which I used quite recently, which can be beautifully coded in one line.

for(int mask = 0; mask < (1<<N); mask++) ans += F[mask] * (__builtin_popcount(mask) & 1 ? 1 : -1);
→ Reply
»
9 years ago, # |
← Rev. 2   Vote: I like it +13 Vote: I do not like it

Code computing zeta and mi transformations (zeta(mi) = mi(zeta) = Id) — look at explanation here: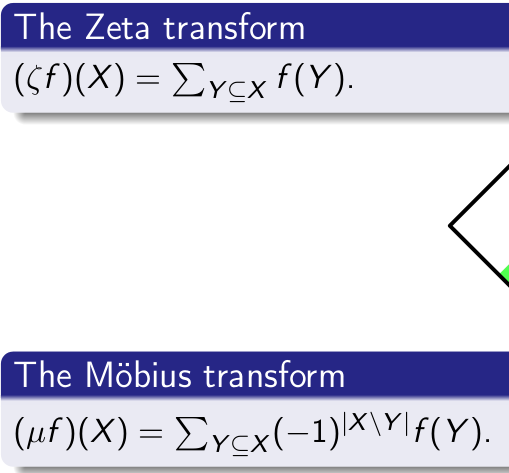 

void Yates(vector<uint>& vec, int sign, int n) {
  REP (i, n) {
    REP (mask, 1 << n) {
      if (!(mask & (1 << i))) {
        vec[mask + (1 << i)] += sign * vec[mask];
      }
    }
  }
}

sign = 1 for zeta and sign = -1 for mi :)

→ Reply
»
9 years ago, # |
  Vote: I like it +3 Vote: I do not like it

Even since I learned about it, I've always been captivated by the magic of DSU.

int find(int n)
{
    return Par[n] == n ? n : Par[n] = find(Par[n]);
}

void union(int a, int b)
{
    Par[find(a)] = find(b);
}
→ Reply
»
9 years ago, # |
  Vote: I like it 0 Vote: I do not like it

I like this implementation of Burunduk1.

Returns next integer in input.

inline int nextInt () {
	int s = 1, x = 0, c = getc(stdin);
	while (c <= 32)
		c = getc(stdin);
	if (c == '-')
		s = -1, c = getc(stdin);
	while ('0' <= c && c <= '9')
		x = x * 10 + c - '0', c = getc(stdin);
	return x * s;
}
→ Reply
»
9 years ago, # |
← Rev. 2   Vote: I like it +5 Vote: I do not like it

Check if a number is even: ~x & 1

→ Reply
»
9 years ago, # |
  Vote: I like it +27 Vote: I do not like it

Here's a piece of code that does some magic. Can you find out what it is? The input is a sequence V of nonnegative integers.


a = 0
while max(V) > 0:
    C = [ 0 ] * max(V)
    for x in V:
        if x%2==0:
            a += C[x//2]
        else:
            C[x//2] += 1
    V = [ x//2 for x in V ]
print(a)
→ Reply
»
9 years ago, # |
  Vote: I like it +40 Vote: I do not like it

Binary search 

while (l + 1 < r) {
    (f(m = (l + r) >> 1) ? r : l) = m;
}

printf("%lld", f(l) ? l : r);
→ Reply
  • »
    »
    9 years ago, # ^ |
      Vote: I like it +47 Vote: I do not like it

    Quickly! Downvote it as fast as you can — the sooner we make it hidden the less people will see this and will code like that!

    → Reply
    • »
      »
      »
      9 years ago, # ^ |
        Vote: I like it +65 Vote: I do not like it 
      #define m ((l+r)/2)
 
int a[N*4];
 
int go(int n,int l,int r,int k,int p,int t)
{
    return t ? p < l || k > r ? 0 : k <= l && r <= p ? a[n] : max( go(n*2,l,m,k,p,1), go(n*2+1,m+1,r,k,p,1) ) : r < k || k < l ? a[n] : l == r ? a[n] = p : a[n] = max( go(n*2,l,m,k,p,0), go(n*2+1,m+1,r,k,p,0) );
}

      What is happening to me ? :'(

      → Reply
      • »
        »
        »
        »
        9 years ago, # ^ |
          Vote: I like it +11 Vote: I do not like it

        Malbolge is a language deisgned to be the worst ever.

        Apparently, it failed.

        → Reply
»
9 years ago, # |
← Rev. 2   Vote: I like it 0 Vote: I do not like it

Opps, some one added it before :P

→ Reply
»
9 years ago, # |
← Rev. 2   Vote: I like it +1 Vote: I do not like it 
int Max(int x, int y) { return (((y-x)>>(32-1))&(x^y))^y; }
int Min(int x, int y) { return (((y-x)>>(32-1))&(x^y))^x; }
→ Reply
»
9 years ago, # |
  Vote: I like it 0 Vote: I do not like it 
c[0], r[1] = 1, 1
for i in range(2, maxn):
    r[i] = (mod - (mod // i) * r[mod % i] % mod) % mod
    c[i - 1] = c[i - 2] * (4 * i - 6) * r[i] % mod

с[i] — i-th Catalan number modulo mod

→ Reply
  • »
    »
    9 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    How often do you use Catalan's numbers?

    → Reply
»
9 years ago, # |
  Vote: I like it -8 Vote: I do not like it 
for (int i = 0, a, b; i < sz (e); i++)
        (a = p (e[i].sc.fs)) != (b = p (e[i].sc.sc)) ? u (a, b), res += e[i].fs : 0;

Kruskal algorithm with DSU.

→ Reply
»
6 years ago, # |
  Vote: I like it +10 Vote: I do not like it

Considering the power of Python... I like my solution of Timus 1067

from collections import defaultdict
from functools import reduce


def recursive_defauldict():
    return defaultdict(recursive_defauldict)


def out(d, dep=0):
    for outer, inner in sorted(d.items()):
        print(' ' * dep, outer, sep='')
        out(inner, dep + 1)


paths = recursive_defauldict()
for i in range(int(input())):
    reduce(lambda directory, name: directory[name], input().split('\\'), paths)
out(paths)

Well, the part with reduce, maybe, is not perfectly readable, but the main trick is recursive_defauldict.

→ Reply