Hi everyone!
Today I want to talk about one quite famous and interesting problem.
So, here it is: given string S. Split it in the minimum possible amount of palindromic strings. Rather unpretentious, isn't it? You can find this problem here or here. But whenever you see it, in the best case intended solution would be a quadratic (or even cubic). Here will be described a solution to this problem in  online (ie, answer will be received for each prefix).
online (ie, answer will be received for each prefix).
Generally speaking, this solution is relatively new and it is not unique (here is the other one quite new though). You can see original droptable's entry here. In this solution palindromic tree will be used, its description can be found in this article. This implementation will be taken as basic.
Let's get started :) To begin with, consider the following naive algorithm runs in O(n2). We will maintain the dp of ans(i) — the minimum number of palindromes, in which you can split the strings prefix, ending at position i. For it will be built palindromic tree and at each step the whole suffix path will be traversed, moving from the vertex to its suffix link.
for(v = last; len[v] > 0; v = link[v])
ans[i] = min(ans[i], ans[i - len[v]] + 1);
To solve the problem quickly, let's introduce two new values that will be stored in the tree vertices difference of vertex diff(v) = len(v) - len(link(v)), and serial link slink(v). Serial link will lead from the vertex v in the vertex u, corresponding to the maximum suffix palindrome of v, which satisfies diff(v) ≠ diff(u). It is easy to see that it is possible to maintain when you create a new node as follows:
if(diff[v] == diff[link[v]])
slink[v] = slink[link[v]];
else
slink[v] = link[v];
Approval 1: path within serial links to the root contain only  vertices. You can see the proof in droptable's entry.
vertices. You can see the proof in droptable's entry.
Knowing this fact you can use following algorithm:
Starting from the maximum suffix palindrome (last), quickly improve answer along all palindromic suffixes till the serial link, and then move on by the serial link and repeat the procedure. It is easy to see that all palindrome suffixes will be considered. Let us learn how to quickly process described set of palindromes (let's call it a series). For this we need
Approval 2: Let us consider suffix palindrome v and link(v) ≠ slink(v) in some step of the algorithm. Then, the previous occurrence of link(v) in a string was in position i - diff(v), while in this position there is no suffix-palindrome with length len(link(v)) + diff(link(v)), ie, link(v) was the beginning of the series in that position.
Proof: Since the suffix of palindrome is also a prefix for him, we can specify the occurence of link(v) in mentioned position as a prefix of v. Let's show that there is no occurence of link(v) between i and i - diff(v). Let's assume there is. Then the intersection of occurences in this position and in the position i - diff(v) is also a palindrome (since it is itself a border of palindrome) with length greater than len(v) - 2·diff(v). So, diff(link(v)) neqdiff(v), it's a contradiction.
Let's show that string with length len(v) ending at i - diff(v) is not a palindrome. Let v = DTDT, link(v) = TDT = DT. From here you can see that if we append diff(v) characters to the front of link(v) and got a palindrome, then appended characters are equal D. But due to the fact that the DT is a palindrome, we see that DDTDT is also a palindrome. Therefore, v is not the beginning of the series, so you will not consider this string on any step of the algorithm.
Based on the approval 2, let's use following dp: Let series(v) is a series, starting at the vertex v, then the value of the dp in it equal
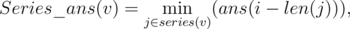 where i is the latest (among already used) position in a string, in which vertex v corresponded to the longest palindrome in series. You can see that when we are in the position i, then series_ans(link(v)) due to approval 2 covers all the values we are interested in, but one in which the length of the suffix is $len(slink(v)) + diff(v)$, ie, considered all palindrome suffixes, except the smallest in the series. It can be considered separately.
where i is the latest (among already used) position in a string, in which vertex v corresponded to the longest palindrome in series. You can see that when we are in the position i, then series_ans(link(v)) due to approval 2 covers all the values we are interested in, but one in which the length of the suffix is $len(slink(v)) + diff(v)$, ie, considered all palindrome suffixes, except the smallest in the series. It can be considered separately.
Finally we have following algorithm:
for(v = last; len[v] > 0; v = slink[v])
{
series_ans[v] = ans[i - (len[slink[v]] + diff[v])];
if(diff[v] == diff[link[v]])
series_ans[v] = min(series_ans[v], series_ans[link[v]]);
ans[i] = min(ans[i], series_ans[v] + 1);
}
Obviously, it works in O(nt), where t — is the maximum possible length of "serial path" ie total complexity is  .
.
An example of a program that prints for each prefix minimal number of palindromes, by which it can be split: #xE2k6Y










Thank you so much..