Div2B — Bear and Three Musketeers
Warriors are vertices and "knowing each other" is an edge. We want to find connected triple of vertices with the lowest sum of degrees (and print sum - 6 because we don't want to count edges from one chosen vertex to another).
Brute force is O(n3). We iterate over all triples a, b, c and consider them as musketeers. They must be connected by edges (they must know each other). If they are, then we consider sum of their degrees.
We must notice that there is low limit for number of edges. So instead of iterating over triples of vertices we can iterate over edges and then iterate over third vertex. It gives us O(n2 + nm) and it's intended solution. To check if third vertex is connected with other two, you should additionally store edges in 2D adjacency matrix.
It's also possible to write it by adding "if" in right place in brute forces to get O(n2 + nm). Check it out in code.
Any positive integer number can be factorized and written as 2a·3b·5c·7d·....
We can multiply given numbers by 2 and 3 so we can increase a and b for them. So we can make all a and b equal by increasing them to the same big value (e.g. 100). But we can't change powers of other prime numbers so they must be equal from the beginning. We can check it by diving all numbers from input by two and by three as many times as possible. Then all of them must be equal. Code
Alternative solution is to calculate GCD of given numbers. Answer is "YES" iff we can get each number by multiplying GCD by 2 and 3. Otherwise, some number had different power of prime number other than 2 and 3. Code
In one operation the highest block in each tower disappears. So do all blocks above heights of neighbour towers. And all other blocks remain. It means that in one operation all heights change according to formula hi = min(hi - 1, hi - 1, hi + 1) where h0 = hn + 1 = 0. By using this formula two times we get height after two operations: hi = max(0, min(hi - 2, hi - 1 - 1, hi - 2, hi + 1 - 1, hi + 2)) and so on. From now I will omit max(0, ...) part to make it easier to read.
After k operations we get hi = min(Left, Right) where Left = min(hi - j - (k - j)) = min(hi - j + j - k) for 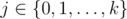 and Right is defined similarly. hi becomes zero when Left or Right becomes zero. And Left becomes zero when k = min(hi - j + j) — we will find this value for all i. If you are now lost in this editorial, try to draw some test and analyze my formulas with it.
and Right is defined similarly. hi becomes zero when Left or Right becomes zero. And Left becomes zero when k = min(hi - j + j) — we will find this value for all i. If you are now lost in this editorial, try to draw some test and analyze my formulas with it.
For each i we are looking for min(hi - j + j). We can iterate over i from left to right keeping some variable best:
best = min(best, h[i]);
best is answer for i;
best++;
We should to the same for Right and take min(Left, Right) for each i. Then final answer is maximum over answers for i. Code
Let's consider a tree already drawn on a strip of paper. Let's take first vertex on the left and last vertex on the right (in case of two vertices with the same x, we choose any of them). There is a path between them. Let's forget about vertices not on this path. A path divides a strip into 1D regions.

What can be added to the main path? Only simple paths attached to it with one edge. So it can be one of the following structures — Y-letter or Line:

Note that Y-letter can have long legs but its central part can have only one edge.
How to check if given tree is a path + Y-letters + Lines? First, let's move from each leaf till we have vertex with degree at least 3, marking vertices as deleted. We don't mark last vertex (that with degree at least 3) as deleted but we increase his number of legs. Finally, for each not-deleted vertex we count his not-deleted neighbours for which degree - min(legs, 2) > 1 — otherwise this neighbour is start of Line or Y-letter. Each vertex on the main path can have at most two neighbours that also belong to the main path. There can be more neighbours but they must be in Lines or Y-letters — that's why we didn't count them. So answer is "No" iff for some vertex we counted more than two neighbours. Code
Let's sort warriors and horses separately (by strength). For a moment we forget about forbidden assignments. Inversion is a pair of warriors that stronger one is assigned to weaker horse. We don't like inversions because it's not worse to assign strong warriors to strong horses: A·B + a·b ≥ A·b + B·a for A ≥ a and B ≥ b. Note that repairing an inversion (by swapping assigned horses) decreases number of inversions — prove it by yourself (drawing a matching with intersections could be helpful). Without any restrictions the optimal matching is when we assign i-th warrior to i-th horse (indexed after sorting) — to get no inversions.
Let's go back to version with forbidden connections. We have n disjoint pairs which we can't use. We will prove that there exists an optimal assignment where (for all i) i-th warrior is assigned to j-th horse where |i - j| ≤ 2.
Let's take an optimal assignment. In case of ties we take the one with the lowest number of inversions. Let's assume that i is assigned to i + 3. There are at least 3 warriors j > i assigned to horses with indices lower than i + 3. So we have at least 3 inversions with edge from i to i + 3 (warriors on the left, horses on the right):
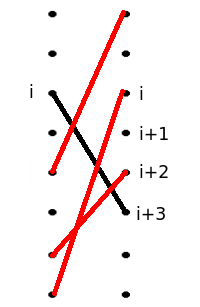
Above, connection warrior-horse is an edge. Then inversions are intersections. Swapping horses for warriors i and j (where j belongs so some red edge) would decrease number of inversions and it wouldn't decrease a score. We took an optimal assignment so it means that it's impossible to swap horses for them. Hence, for each red edge we can't change pair (black, read) into the following blue edges:
So one of these blue edges is forbidden. Three red edges generate three pairs of blue edges and in each pair at least one blue edge must be forbidden. Note that all six blue edges are different. All blue edges are incident to warrior i or to horse i + 3 but only one forbidden edge can be incident to warrior i and only one forbidden edge can be incident to horse i + 3. We have at most two forbidden edges incident to them so it can't be true that three blue edges are forbidden.
By cases analysis we can prove something more — that there can be only three possible types of connecting in an optimal assignment. First type: i can be connected to i. Second: warrior i with horse i + 1 and warrior i + 1 with horse i. Third: warriors i, i + 1 and i + 2 are connected with horses i, i + 1, i + 2.
It gives us O(nq) solution with calculating queries independently with dp[i] defined as "what result can we get for assigning everything with indices lower than i?". To calculate dp[i] we must know dp[i - 3], dp[i - 2] and dp[i - 1]. It wasn't intended solution because we can get better complexity.
We can create a segment tree and for intervals we should keep info "result we can get for this interval with 0/1/2 first and 0/1/2 last elements removed". For an interval we keep matrix 3x3 and actualizing forbidden edge for single i consists of: 1. calculating values of 3x3 matrix for a small interval with i 2. actualizing a tree with  times multiplying matrices
times multiplying matrices
Complexity is 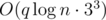 .
.
FIRST PART — greedy works
We will add (take) elements to a subsequence one by one. Adding number x, when we have k - 1 taken numbers on the left, increases result by k·x + suf where suf is sum of taken numbers on the right. Let's call this added value as the Quality of element x.
We will prove correctness of the following greedy algorithm. We take element with the biggest Quality till there are no elements left. For every size of a subsequence (number of taken elements) we will get optimal score.
(lemma) If ai > aj and i < j, we won't take aj first.
Proof. Let's consider a moment when we don't fulfill the lemma for the first time. If there are no taken numbers between ai and aj, we have Qi = k·ai + suf > k·aj + suf = Qj so ai is a better choice. For taken numbers between ai and aj — each number x changes Qi by x and Qj by aj. We'll see that x > aj so Qi will remain greater than Qj. If ai > x, the lemma (fulfilled till now) says that x wasn't taken before ai — it can't be true because x is taken and ai is not. So indeed x ≥ ai > aj.
Let's assume that our greedy strategy is not correct. Let's consider first moment when we take some element aj and for some s we can't get optimal subsequence with size s by taking more elements (using any strategy). Let A denote a set of elements taken before. So there is no way to add some more elements to set A + aj and achieve optimal score with size s. But it was possible just before taking aj so there is a subset of remaining elements B that |A + B| = s and set A + B is the best among sets with size s. Note that B can't be empty.
(case 1 — B contains at least one element on the left from aj) Let ai denote last element from B that i < j (here "last" means "with the biggest i"). Our strategy wanted aj before elements from B so we know from lemma that ai ≤ aj. It will turn out that replacing ai with aj (in set A + B) doesn't decrease the score so taking aj is acceptable. Note that replacing an element with another one doesn't change size of a set/subsequence.
In moment of choosing aj it had the biggest quality so then Qj ≥ Qi. Now in A + B there are new elements, those in B. Let's imagine adding them to A (without ai and aj). Each new element x on the right change both Qi and Qj by x. Elements on the left change Qi by ai and Qj by aj (note that ai ≤ aj). And there are no elements between ai and aj. Now, taking ai would give us set A + B but Qj remains not less than Qi so we can take aj instead.
(case 2 — B contains only elements on the right from aj) Similarly, we can replace ai with closest aj from set B. As before, elements on the right change Qi and Qj by the same value.
SECOND PART — how to implement it
First, let's understand 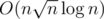 solution. We divide a sequence into
solution. We divide a sequence into  Parts. When choosing the best candidate in a Part, we want to forget about other Parts. It's enough to remember only x and suf — number of taken elements on the left (in previous Parts) and sum of elements on the right (in next Parts). x affects choosing the best element in a Part, suf doesn't (but we need this constant to add it to result for best candidate). For a Part we want to have hull with
Parts. When choosing the best candidate in a Part, we want to forget about other Parts. It's enough to remember only x and suf — number of taken elements on the left (in previous Parts) and sum of elements on the right (in next Parts). x affects choosing the best element in a Part, suf doesn't (but we need this constant to add it to result for best candidate). For a Part we want to have hull with  linear functions of form ai·x + b. With binary search we can find the best element in
linear functions of form ai·x + b. With binary search we can find the best element in 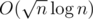 and then construct new hull for this Part in
and then construct new hull for this Part in 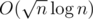 .
.
We can remove 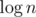 from complexity. First, binary search can be replaced with pointers — for each Part initially we set a pointer at the beginning of Part. To find best candidate in Part, we slowly move pointer to the right (by one). Complexity is amortized
from complexity. First, binary search can be replaced with pointers — for each Part initially we set a pointer at the beginning of Part. To find best candidate in Part, we slowly move pointer to the right (by one). Complexity is amortized 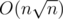 . And we can sort linear functions ai·x + b by angle only once because value ai doesn't change — then constructing a hull is only
. And we can sort linear functions ai·x + b by angle only once because value ai doesn't change — then constructing a hull is only 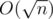 . Note that when rebuilding a hull, we must set pointer to the beginning of Part.
. Note that when rebuilding a hull, we must set pointer to the beginning of Part.
So we have 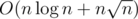 . Code.
. Code.
There are other two correct lemmas to speed your solution up. We can take all positive numbers first (it's not so easy to prove). And we can stop when taken number doesn't increase score — next taken numbers won't increase score neither.











Wow super fast editorial! Thank you! :)
I think it waa a balanced contest, though bit on easier side. I think div 2 B was a bit harder than usual..
but had fun solving for 1 hour, but internet slow + hang meant I could not do last hour. tomorrow I do on practice
WAT? balanced ? div 1 A,B was solved ~1000,800 and div 1 C ~ 200.
About div1C: We can have unlimited chains(a leave and some vertices with 2 edges each) in original graph, they fall in one line. So we delete any chains and only left vertices are ones that had 3 or more edges in original graph. Then we can either have a long chain out of left vertices, or direct leaf to the chain that used to be 3-edged vertice.
I have thought of this as well. This is what I implemented: 1) Remove all vertices of degree 2 by connecting the two neighbours directly 2) Output "No" when there is a vertex X that has more than two neighbours Y_i such that — Y_i have more than 3 neighbours (including X) OR — Y_i have neighbours other than X that are not leaves.
It does not pass. Can anyone please point out what's wrong with it?
OK, got it. In step (1) I can only remove vertices of power 2 when there is a leaf at least on one of the sides. Removing intermediate nodes between "junctions" may change the outcome.
For example in the sample test #2 if we remove node 8 the anwer will change to "Yes". But it we then insert another node between 1 and 3 the answer will change back to "No"...
Can anyone please tell why my submission is giving runtime error? It is working fine on my local ide.
Submission link : http://codeforces.com/contest/574/submission/12757848
I send your solution with GNU C++ and it has WA 13. It is really strange. I don't know your bug exactly, but i think it in lower_bound. Here is my submission with some improvments of your code. You don't need this if(p[j].second == b). 12766037
In line 70 you should write vector q(n,0) instead vector q(m,0) i suppose.
could anyone help me find my bug plz? :| 12751097
You should add:
since it's an undirected graph.
you should add arr[b][a] = 1. Oh, i haven't seen the previous commnet
OUCH! really it was that? :)) Tnx guys.
12765618
what is special about test #12 in div1C?
One need to start dfs in vertex with degree 4, not 3 on that test. (and that is not true anyway but passes)
Starting dfs from vertex with degree >=4 instead of >=3 doesn't seem like an optimizaton which can turn incorrent solution into correct one ( ͡° ͜ʖ ͡°)
well, considering that vertex with degree 4 is always on main path and vertex 3 is not...
But there are cases where there aren't nodes with degree >= 4 and the answer is no.
Why does this approach fail for Div2C?
The idea is very similar to a question asked in a recent contest, called "Amr and Chemistry". In this question ,we can run BFS on all the initial nodes(initial bids) and at every stage and add 2*current bid and 3*current bid into the queue until the queue is empty. This is because this would list out all the bids/nodes reachable from the present initial nodes. We do this for all bids
What we do meanwhile is we keep a Map for storing the count ALL the vertices visited, be it from any initial bid. If in the end, the the count of any vertex in the map is equal to 'n', this means that every initial bid can reach this bid, hence the answer is 'Yes'. If the count for no vertices is 'n', the answer is 'No'. My solution fails on pretest 7. I have absolutely no idea why. Any help is appreciated.
Solution: (http://codeforces.com/contest/574/submission/12751820)
A random guess is that the bids overflow the limit of the variable you're using. Because as opposed to Amr and Chemistry, where you divide (so no overlow), you multiply over and over, and when bids start at 10^9, the 'answer' you are looking for could be insanely large (pretest 7 has 100,000 numbers, so the answer is almost certainly really large)
Fails for
2
14 21
also for
2
2^26 3^16
Your solution is not feasible even if you set your maxv to 10^16
Your code gives bad answer on case:
2
2 3
It's possible, because 2 * 3 = 3 * 2, but your code outputs 'No'.
I think it's because you compare cv with max. Here is a modified code which outputs correct answer: http://ideone.com/P3fxBd (I'm not sure it's 100% correct)
Can someone please explain Div1 B in simple terms? Thanks.
Try to find biggest triangle(something like: 1 2 3 4 ... h ... 4 3 2 1) from the given input. This triangle needs h steps. The biggest triangle will disappear the last and its h is the answer.
I can't understand it too!
but,I hope my solution can help :
you can calculate whole destroy time for all towers from left and right separately.
assume these : destroyTimeL[0] = 0; destroyTimeR[n+1] = 0;
for left, each tower will be destroy in this time : min( destroyTimeL[i-1]+1 , height[i] );
for right : min( destroyTimeR[i+1]+1 , height[i] );
so minimum of these values is valid destroy time for tower.
now you can get maximum of them as answer.
12759208
very nice.
Got it.
Respect for such a nice approach....
What elegant method,beautiful solution!! I am a beginner and your solution is very elegant to me!! blew my mind, How did you think of this?what was your thought process behind this DP, Please help me,and sorry for commenting on a 2year old post..
Maybe my implementation can help you: 12766704
Little mistake in editorial: best = min(best, hi)
Trying explain by words:D
Let's imagin blocks may not adjacent to other block by right side. Then for first sample:
0) 2 1 4 6 2 2
1) 0 0 1 4 1 1
2) 0 0 0 1 0 0
3) 0 0 0 0 0 0
For each tower you need just min(h(i — j) + j) for j = 0..i operations
Analogically if blocks may not adjacent to other block by left side then for tower i you need min(h(i + j) + j) for j = 0..n — i — 1
And answer is max(min(left(i), right(i))) for i = 0..n — 1
Try to find the last node(square) that is going to be deleted. It is easy to check that the time when the node is going to be deleted is just the shortest distance of the node to the outside. In each column the last node to delete is alway the one in the bottom, so you only need to calculate the shortest distance for each bottom node to the outside. The shortest distance is going to be:
min( 1 + shortest_distance_of_left_neighbour,
you may solve it using simple dp in two iterations.
Ahh, missed this observation :( Pretest #5
It seems that problem E has some other interesting solutions: 12759251, 12764750, 12760770
What's going on in the third summission? It seems some standart c++ things. logicmachine can you explain it, please!
Have you ever seen such lines before in CF codes?
SSE instructions They allow vectorizing the code (process 4 numbers simultaneously and thus the program is 4 times faster).
Oh, wow, someone got a SIMD-based solution through. Major props. I'm somewhat surprised it was possible, given that the problem involved 64-bit integers and that Codeforces lacks support for AVX.
I think I have done what the editorial describes in my solution for Div2B but somehow my code times out. Could someone please have a look? http://pastie.org/10384203
Don't use set. It's too slow there
I've used set and it works fine 12751433
I used set. http://codeforces.com/contest/574/submission/12765191
Will be no russian editorials in thanks-rounds?
Tourist at 168. position and my two friends at positions 1. and 2., What is going on, I don't even :P
I didn't really get
"How to check it"in Div1C. Could you explain, please?Great problems and great editorial
Problem A Div1 can be solved by dividing all the numbers by
2ifa%2==0and then dividing by3ifa%3==0then , if all numbers are equal then the answer is Yes and No otherwise.It's a rare case when I fail at the contest, but still like the problemset :)
good to hear!
Weak tests in problem E. I've got AC with this easy and wrong approach:
First, take all non-negative numbers. After that, lets walk from left to right and from right to left and take(or un-take) negative numbers if that increases total score. That gets AC on codeforces and fails locally on stress very quickly =/
stress testing is easier when we get a code :/ but I feel bad about wrong solutions passing.
I can only say that I'm sorry.
I do not understand why my solution is wrong!? FOr Div2 B My approach : 1) Find cycles of length 3 using DFS . Each Back Edge will tell me that cycle is of length 3 iff difference of Level of the current Node and the node with which this node shares an edge is 2 !
2) Now the degree going out of this is Sum of Degree's of this Node ,parent of this Node and Degree of the Node connected with back edge — 6 ( Internal Degree )
Now take the maximum ! My code gives a WA ! I cannot understand why ? 12754070
hi i too tried the same approach and it intuitively seems right but int the test case where your code is collapsing there is certainly a cycle of 3 members(4- 15-6) and somehow your dfs fails to detect it
because when you reach the intended nodes, the value of their levels might not be what you seek for (difference=2) because you may visit the same nodes you search for but by other long paths, so in test case 13 there's a cycle of length 3: {15,6,4} but you reach 15 you go then to 6 and then you go to 4 by some other path and mark "4" as visited and give it a big level , So when you come back to 6 and try to go to 4 (and check it's level) the difference will not be 2
Got it ! Thanks !
By the Way I didn't proved my approach of taking the difference of level!
I had solved a similar problem but the graph would have had been a tree Then this approach works!!
Sad!!
Could anyone explain me why do I get the WRONG_ANSWER for the div2-B for the test 12? When I run the same input on my local machine, I get the right output ("2"), but it's different on the codeforces test 12. How could it be and how do I resolve it? (I use compiler GNU G++). I just can't figure out the cause of the problem on my own. Thanks.
The link to my submission: http://codeforces.com/contest/574/submission/12759200
http://codeforces.com/contest/574/submission/12766711 Here is your accepted solution i just un-commented the 'cerr' something that you were printing.
Upd: there was a bug in my code. Finally, I found it.
now i am curious to know what it was and how commenting that specific line avoided it!
Try declaring that big array as a global one, not local (very doubtful about significance of that cerr brighterstill mentioned, probably his submission passes because of compilator change, but don't have time to verify everything).
http://codeforces.com/contest/574/submission/12757696
Can anyone see my solution for Problem A Div1? I am getting wrong answer but i am not able to figure out why its failing?
I took lcm of all numbers and then divided this lcm by every number.Now The numbers which i got after dividing : i am checking whether there is prime factor other than 2 and 3 in those numbers.If yes then answer is "No" otherwise "Yes"???
Help Plz :(
lcm of 10**5 numbers of order 10**9 would go way beyond the limit of long long or any other datatype!
In editorial for problem Div1-B it says best = max(best, hi) but it should be best = min(best, hi) instead.
"Let's sort warriors and horses. It can be proved that there is an optimal assignment that assign very near (+-2) things. Solution is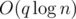 with big constant factor."
with big constant factor."
This is the editorial? :>
No but it's still more than editorial for div2A :/
I will try to write it in two hours.
EDIT: will be added tomorrow, sorry for delay.
My O(nlogn) solution to div1.E:
Consider the dp solution: dp[# of rolls], which means the maximum score with certain number of rolls so far.
How a_i update the sequence: if(dp[k]+(k+1)*a_i>dp[k+1]) dp[k+1]=dp[k]+(k+1)*a_i
Create a "threshold" sequence: th[k]=(dp[k]-dp[k-1])/k. dp[k] should be updated if and only if a_i>th[k]. Let's see how to update th[k]:
if(a_i>th[k-1] && a_i>th[k]) th[k] = (th[k-1]*(k-1)+a_i)/k (both dp[k-1] and dp[k] are updated)
if(a_i<th[k-1] && a_i>th[k]) th[k] = a_i (dp[k] is updated, but not dp[k-1])
An important observation is, th is always in descending order. This can be proved by math induction based on the update condition above. Now discard the dp sequence, because it can be deduced from th. We can maintain th by BST with following operations:
Find the position where a_i<th[k-1] and a_i>th[k]: O(log n)
Insert a node with key=a_i
If we use the pair (th[k]*k,k) to represent th[k], th[k+1] will become (th[k]*k+a_i,k+1). Thus, we can use the node which initially represent th[k] to represent the newly updated th[k+1]. All nodes after this position can be updated by some lazy implementation.
Finally, reconstruct dp based on th and find the maximum value.
I have a solution for C but I don't fully understand why it's correct. First fix the root the tree at each node step by step. Now for every root count the number of neighbors who either have their degree >3 or there is a node in their subtree with degree >2. If the number of such neighbors is >2 than return No. After checking all nodes and the none satisfied the conditions above, than return Yes. Here is my code: 12767021
My Div1 B, featuring Dijkstra: 12748563 ( ͡° ͜ʖ ͡°)
Yeah I too used a similar approach, the only difference being I used a Set instead of a Priority Queue.Link to code ( ͡° ͜ʖ ͡°)
I don't understand it. Can you explain? It seems a very interesting idea :)
I solved div1 B using Dijkstra too. Here is my idea.
If a tower gets destroyed in time t, then its adjoining towers will be destroyed in time <= t+1, so you can think of destruction as something propagating with speed 1 tower/sec. Also, if a tower is of height h, then it will take time <= h to be destroyed.
So a tower will be destroyed by whatever happens first, destruction reaches it from some neighboring tower or it is destroyed because of its height. Now you can solve this using dp, as shown in the editorial, or model it as a weighted graph in the following manner.
Run Dijkstra from source node and the distance to each tower is the time at which it gets destroyed.
Source: 12755104
The idea is that a block will disappear after K steps, where K is the length of the shortest path from that block to the outside of the figure.
With some optimizations we can compute the shortest paths fast enough:
The graph is simplified to one of linear size and we can run Dijkstra's.
In div2B, My code is giving WA on tc 15. I am not able to debug. Can anyone help with this? http://codeforces.com/contest/574/submission/12767413
Anybody has an idea why this solutions fails? http://codeforces.com/contest/574/submission/12768336
I'm basically running DFS from every node that has not been seen in a previous DFS ( so in total I only enter a node once).
I keep track of the parent node.
If the current node is directly connected with another node that has a direct edge with the parent. ( and ofc not the parent itself). I will minimise on the summation of their degree-6.
However this gives WA on test #21. The test case is too big and not even full, so I can't trace it.
Would appreciate the help.
since when did codeforces editorial start to include code, a really good move for beginners, thank you.. :)
I think the solution for Div2-B where we iterate for the edge and then for the third vertex is O(m * n). Am I right? 12755700
in problem Div1C — Bear and Drawing judge solution prints "Yes" for this case
but i think the answer is No. please correct me if i'm wrong.
look at the picture
I don't understand the tutorial for DIV2 #5. I even didn't understand why the Answer is No for the second sample test case of the same problem. I tried to understand that during contest as well :).
What is wrong with the solution in the image? Sorry for asking very basic questions but I'm trying to understand it from last couple of hours.
Edges must be lines
http://codeforces.com/contest/573/submission/12766903
http://codeforces.com/contest/573/submission/12766685
Update: It turns out Xor128 was just a pseudo random number generator, he used it for debugging... But his algorithm (in the function
solve()) still remains unknown to me! Plus, it seemed that his algorithm is O(n2) (not taking the weird Assembly / internal function code complexity) and he ran it in 3s... How?I came across these solutions (from anta) for problem Div1E. It seemed he used some sort of algorithm named "Xor 128" (?) which I have never seen before. Furthermore I could not understand anything from his function
solve(). It looks like Assembly, I guess.Please explain your solution, anta please!
About the first solution, I just used SSE intrinsic functions for speed up n^2 loop. About the second solution, I just replaced intrinsics to inline assembly in order to be work in G++.
I have coded the first solution during the contest. However, because compiler option of G++ on Codeforces server is not sufficient to use SSE4 intrinsics, I needed to rewrite it to something that can compile on Codeforces server.
In fact, the code can be compiled in MSVC++ but I forgot that MSVC++ exists on Codeforces. Also, I didn't known how to write G++ inline assembly instead of intrinsic functions.
After the contest, I figured out way to run my code in two ways (it is the submissions).
So, I lost a big chance of become the winner of the contest.
Errichto can you prove the correctness of your logic to div1 B? In particular, I am not comfortable with this formula:
hi = max(0, min(hi - 2, hi - 1 - 1, hi - 2, hi + 1 - 1, hi + 2))
I think it should be :
hi = smallest positive out of (hi - 2, hi - 1 - 1, hi - 2, hi + 1 - 1, hi + 2).
Or am I missing something?
edit: After k operations we get hi = min(Left, Right) where Left = min(hi - j - (k - j)) = min(hi - j + j - k) for 0<=j<=k
what if h(i-j) is already 0, the above idea won't apply. How are you accounting for the times when h(i-j) is already 0?
edit2 : Ok, I understood :)
In the solution for problem Div 2 B Bear and Three Musketeers,i eventually got the solution during the contest but i have a doubt,I wrote the following solution which uses map with pair<int,int> http://codeforces.com/contest/574/submission/12759418
I don't understand how it give memory limit exceeded error, And more over i don't really understand how memory is filled in the 2-d map and why did it got exceeded, can someone please explain how it work?
And if the memory always exceeded in such a way as i have mentioned then maybe one should never used 2-d Map as 2-d Array consumes less memory and answers the query in O(1) , can anyone clarify this and also how 2-d map actually works?
So answer is "No" iff for some vertex we counted more than two neighbours ->
So answer is "No" if for some vertex we counted more than two neighbours
I think iff means if and only if.
Can someone explain the implementation of Bear and Blocks for this solution 12767308
For Div2:B Bear and three musketeers I tried sorting by degree and exiting as soon as I find the first triplet that is connected, why does this not work ? We are looking for min (o1 + o2 + o3) where o1, o2, o3 are the connected neighbors. But brute force works fine.
Sorted and exit early version: http://codeforces.com/contest/574/submission/12778361
Brute force: http://codeforces.com/contest/574/submission/12778311
Because you first find the triple with the lowest o1, not with the lowest o1+o2+o3.
Your "brute force" is O(nm) and is the same as intended solution — read an editorial.
Can any one help me with the bug:Submission -used DFS(upto depth 3) to detect cycle of 3 and then updated minimum sum
You are copying the entire graph in each BFS recursive call. You should call this function passing the graph by reference or have the graph globally declareted. BTW, I think by Bfs you meant DFS.
Oh yes, a stupid mistake to do (:, Thanks and ya I meant DFS
I have wrong answer on test 8 on Div 1 C. I'm searching for the longest chain in the tree and then I check if all remaining chains of nodes can be put on a single line. Source code: https://upl.io/6h8mr4
Could anyone tell me why you take min(legs, 2) in Div. 1 C?
Because Y-letter can have only two legs. When counting degree we skip at most two legs but not more.
I think in "Div2-B, paragraph 3, line 2", "O(n^2 + nm)" should be "O(nm)".
Here is my solution that is "O(nm)":
http://codeforces.com/contest/574/submission/12786795
Allocating the n × n matrix takes Θ(n2) time.
We cannot say allocating matrix takes O(nm) times, Because max(n)=max(m)?
If yes, O(nm)+O(nm)=O(nm).
However, m may be much smaller than n (for example, m = 5, n = 1000). Your program will still need to allocate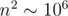 elements, though
elements, though 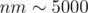 . Θ(n2) component is here way more "important" than Θ(mn).
. Θ(n2) component is here way more "important" than Θ(mn).
574B - Bear and Three Musketeers How O(n^3) works for n = 4000 ?
It gives TLE.
Oh, I see, you said that brute force will not work. my mistake.
Errichto please explain your segment tree solution of div 1 D in detail. I can't understand what exactly you're trying to do there , and I couldn't find any comment here by any user that explains so. Please do explain. I am very interested in knowing what the logic is. :)
For some small segment (stored in a leaf of a segment tree) we calculate answers brutally "max result after removing x first and y last items from this segment" for all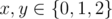 " (let t[x][y] denote this value). We must store it in matrix 3x3.
" (let t[x][y] denote this value). We must store it in matrix 3x3.
Note: It depends on implementation but likely you will want merged intervals to have two common items (e.g. we merge [5,50] and [49,123]).
We want to merge two segments to get answers for sum of them (this way in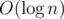 we get answers for whole sequence). To do it, we "multiply" matrices.
we get answers for whole sequence). To do it, we "multiply" matrices.
Lemma about only three possible types of connecting means that answer for we can split interval [5, 123] and its answer is equal to one of ans[5][48] + ans[49, 123] or ans[5][49] + ans[50, 123] or ans[5][50] + ans[51][123]. So t[x][z] of new bigger interval is equal to left[x][y] + right[2 - y][z] for some y.
And, can I have the code please :)
Please :) I didn't find it in your submissions page.
I don't have a code easy to read. Check out submit from someone from the top in contests standings. Maybe mnbvmar's code.
Ok, thanks by the way :)
Thanks for the downvotes -_- . What was my crime?
There is a solution whith O((n + m)*sqrt(m)) for "Bear and Three Musketeers". Let us name the vertex "hard" if its degree is >= sqrt(m). The number of hard vertexes is O(sqrt(m)). The "soft" vertexes have a degree O(sqrt(m)) and the number of them is O(n). So, we can iterate over all edges from each vertex with O((n + m)*sqrt(m)). Letus iterate over edges. If (u, v) — current edge and deg(u) < deg(v) (Or deg(u) == deg(v) && u < v) then let`s iterate over all vertexes connected with u. If x — current vertex && (x, v) in E then we can relax the answer with deg(u) + deg(v) + deg(x). So, we have solution whith O((n + m)*sqrt(m)) complexity. PS: sorry for my poor Englsh=)
PS: we can check if (x, v) in E in O(1) using hash tables or using this trick: initialize used[i] = -1. When we iterate over edge we iterate v and then all edges from it. If (v, u) in edges lets set used[u] = v. Then if we want to check (x, v) in E, we must check (used[x] == v). PS: code goes here http://codeforces.com/contest/574/submission/12804930
Your code is simpler than your explanation :) But from where did you get that complexity? 'At max' sqrt(m) vertices have degree>=sqrt(m). This means, the number of times the k-loop is skipped is at most sqrt(m). So, in average to worst case, complexity is still m*n.
In Div1.D, how to prove that "there can be only three possible types of connecting in an optimal assignment"? I try to prove it by "swapping an inversion", just like how you prove that i cannot connect with i+3, but find a counter example: assignment: (1,3) (2,1) (3,4) (4,2) forbidden edges: (1,1) (2,4) (3,2) (4,3) In this case, we can't swap any inversion, but obviously there is a better assignment: (1,2) (2,1) (3,3) (4,4). Is there any other helpful property?
If I got your question correctly , maybe this will help : In the sorted order of warriors and horses, if any 3 consecutive warriors and corresponding horses(in sorted order) have the forbidden property, then assignment is: (i, i+1) , (i+1, i+2) , (1+2, i). If any 4 consecutive warriors and corresponding horses(in sorted order) have the forbidden property, then assignment is: (i,i+1) , (i+1,i) , (i+2,i+3) , (i+3,i+2). Now I guess you can see the 3 possible types of connecting in optimal assignment.
These assignments are reasonable but I don't know how to prove that "they are always better".
Because, any other matching will increase the number of inversions.
increase the number of inversions != decrease the total strength
No, but we can assign greedily to get the maximum strength. Errichto proved that horse i will always be matched to a warrior j such that |j-i|<=2 for maximal matching, or else, we get contradictions(it will not be maximal). Now, if 5 consecutive pairs are forbidden, what do you think the correct pairing will be? (1,2)+(3,4,5) or (1,2,3)+(4,5) ? We want to multiply a high value on left with highest possible value on right(greedy works, and Errichto proved this too). But, like in the case of 5 consecutive pairs, or 6,and so on, we still need to check which one is optimal. But in no case, do we need to break the condition|i-j|<=2. This condition will hold everytime.
Another example,if i<=N-3, and 3 consecutive forbidden pairs exist (i,i),(i+1,i+1),(i+2,i+2), then what do we do? Do we match (i,i+1)+(i+1,i)+(i+2,i+3)+(i+3,i+2) or do we match(1,2,3) and 4th pair is anyways not forbidden. This is what we can check for optimal strength, but I think its intuitive that |i-j|<=2 in every pairing in optimal matching.
aaaaajack. As I wrote, we can prove it by cases analysis. I don't see nicer way to do it.
If I remember correctly, there are two classes of connecting exactly 4 consecutive warriors and horses and you found one of them. Both of them can be changed into something not worse in terms of "total strength first, then number of inversions".
The other class is assignment (1,3),(2,4),(3,1),(4,2) with forbidden: (1,1),(2,2),(3,4),(4,3).
For more than 4 consecutive things to connect there are the same classes expanded in some regular manner.
I see, thank you. :)
Errichto!
Please explain the proof of that fact: "there can be only three possible types of connecting in an optimal assignment".
There is no strong proof of this fact.
Considering i<=N-3 and 4 consecutive forbidden pairs. In this case, we prefer (i+1,i) over (i+j,i), where j>1 . So we can make that pair. Also, we can make (i+3,i+2) pair(because (i+3,i+1) is not the best matching when (i,i+1) or (i+2,i+1) can be possible). Now its cakewalk to make the other two pairs. Also, we won'e even consider i+4 because including that will introduce 1 inversion, which in this case will decrease max strength.
Please read aaaaajack's comments above and my answer.
Hey, Why is the solution to Div2B Bear and Three musketeers said to take O(n2 + nm). For each edge, we iterate over all vertices. That's O(nm) time. Where does the O(n2) term come from?
Creating array t[n][n] takes O(n2).
No it doesn't if by t[n][n] you mean the adjacency matrix then it can be created in O(M);
int t[MAX][MAX];
int main() { int m; cin>>m; while(n--) { int x,y; cin>>x>>y; t[x][y] = t[y][x] = true; } }
This takes O(m) time.
My O(m*n) solution: http://codeforces.com/contest/574/submission/12986751
I am not getting div. 2 B time complexity I think it should be O(n*n*m) because there are three nested loops and if we take a complete graph in worst case it will take n*n*m operations.Can anyone help me.
for(edge) for(vertex) — two loops
And an alternative implementation has its complexity explained in comments in my code. For each moment (line) think how many times can program be there.
can i get the editorial of div2 problem A ??? I am a beginner in coding and weak in implementation.... help me out plzzz..
In the explanation for E/div2, what is the meaning of "in case of two vertices with the same x, we choose any of them"?
Can any body tell why this O(n^3) solution is accepted (n=4000) ?
Is it the if() that make it faster ?
I submited 2 solution and i only changed the if() statement , first got TLE and the second is AC , i thought that complexity is the same regardless the if() statement , am i missing something ??
Can any body explain ?
Cant Div2B — "Bear and Three Musketeers" problem be solved with a single dfs, with overall complexity being O(N)? Please correct me if I am wrong or missing something.
PS:Errichto can you please help?
I don't know how to do it in O(n). Explain your approach/idea, please.
Start from any vertex(say 1), keep doing dfs, marking each vertex with its level in the dfs tree. We maintain a global variable storing the current minimum value for the answer. If say from a vertex v, there is back edge to u, and abs(level[u]-level[v]) is equal to 2, then it forms a cycle with 3 vertices. Thus, for all such (u,v) we can update the global var (by calculating sum of degree of all 3 vertex subtracted by 6) where needed.
Am i missing anything?
You didn't consider all triangles. For example, let's say from v there is a back edge to u = parent[parent[v]] and an other back edge to w = parent[u]. There is a triangle (u, v, w).
Thank you so much Errichto, I guess this is what I was missing out on.
My understanding of problem B's time Complexity. It's called amortized analysis, the time complexity is different from your first glance. You have to calculate maximal number of times the comparison operator execute as well as the maximal number of times the assigned operator execute and the asymptotic complexity is the maximum of two above values.
Can someone please tell me how can I get the time complexity for my solution for
Div2B — Bear and Three Musketeers85852389I have used dfs to check if there are some cycles of length 3, if it exists, I keep on pushing the tuple to my answer-vector. Finally, I calculate the minimum recognitions of them all
How to use Binary Search for Div 1 B as given in tags?
For problem div1E, I came up a solution which deletes the number from the original sequence with minimum quantity instead of adding the maximum one. Could anyone please prove or hack it?
didn't find out where is your solution
but greedy like https://codeforces.com/contest/573/submission/117013807 (Accepted by main tests)
could be hacked with this
out: 155
ans: 156(with "0 0 0 -5 0 0 0 22" as a result)
seems like main tests not strong enough : /
Why problem E can be solved just using C++20 in $$$O(n^2)$$$
A. Bear and Poker This question 2 3 2 This data can hack my code https://codeforces.com/contest/573/submission/204709133
but O(n^2) brute force dp can pass E
But Div1E can use c++20 and $$$O(n^2)$$$ AC now.