It's sqrt decomposition. It didn't rime. Bummer...
Cutting to the chase
It has been written about sqrt decomposition many times. Still, many people see as a poor cousin of segment trees. Even though segment trees are more frequent in practice and much faster, I think both of them have their own advantages. Comparing a tank with a Ferrari might not be the best metaphor, but it's still applicable to some extent.
Sqrt decomposition is straight forward and easy to understand and yet an useful tool. Playing with data structures might come more natural if you broaden your horizon. One might fight with sticks before using a sword. Though, one might skip stick fighting for some reason and still be an excellent swordsman. Still, fighting with sticks is badass, especially if you're a monk. ### A story about two eggs
You are given one n-story building and 2 identical eggs. There is a number x, such that any egg dropped from a floor lower than x will survive the fall, while any egg dropped from a floor higher than or equal to x will break.
First of all, let's forget about the fact that we have just 2 eggs. Suppose we have n eggs. Let's denote the verification function of an egg breaking down as f. That's how f works for the following example:
stores | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
----------+---+---+---+---+---+---+---+----
f(store) | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 |
The egg will break down at 6-th floor. We can observe that f is a non-decreasing function. That means we can binary search on it. So, one might try to break an egg at 4-th floor , then at 6-th floor and finally 5-th floor.
Let's return to the original problem. You have now only two eggs. How useful is the strategy above ? Well, if the first throw leads to the egg cracking this will reduce our search to half of the stores. You might want to reuse the egg, so this suggests that you have to take a smaller step.
Take a closer look on how splitting the building in two halves work. First throw splits the interval in two, and the second one iterates through the interval. Try to do that with 2 throws with the first egg. So, split the interval in three ( one throw at N/3 , one at 2*N/3 ) and then iterate. Much faster , right ?
We only have left the generalisation of the concept above. But when we stop ? Let's denote X = length of the split. Well, first egg will be thrown N/X times , and the second one X times. Taking X = sqrt(N) will give as a number of O(sqrt N) throws. And that is a little example of what is yet to come.
Note the problem above was used for explicative purposes. For the general case problem look here .
Basics
You are given an array of length n. Answer to m query of types:
- “What is the maximum element in interval [x,y] ? ”.
- The elements on position x take the value y.
The brute force goes like that: we shall iterate from x to y for each query and compute the answer. The update will be O(1) and query O(N). That is O(N*M).
The key element in sqrt decomposition is skipping. Let's define a k-segment as a continuous subsequence from an array that has the length less or equal to k. We shall divide our array in as little k-segments as possible. For example array [1,2,3,4,5,6,7,8,9,10,11,12,13] divided in 3-segments looks like: [1,2,3] [4,5,6] [7,8,9] [10,11,12] [13]. Note that this greedy split of adding elements to a segment if possible ensures us with a maximum number of k-segments.
Now let's apply the k-segment concept to our queries. Let's say we want to find the maximum on interval [3,11]. That is find the maximum out of elements 3] [4,5,6] [7,8,9] [10,11. Let's observe we have “full” and “broken” 3-segments in our example. What is the maximum number of “broken” segments ? It's two ( the left and right border segments ).
Finally , having all this stuff sorted out , I'll present you the final solution.
We record for each segment it's elements and the maximum element. An update is made by replacing the element on the x-th position and updating the maximum on the k-segment. A query can be responded by calculating the maximum on “broken” k-segments and the maximum of the values of the “full” segments.
The complexity is O(K) for an update , O(K+N/K) for a query and O(N) for building the structure. If we take K = sqrt(N) , then the complexity will be O(N+M sqrt N).
Here is an (object oriented) approach to implement the problem above.
You can also read more about the basics (and other stuff) here .
Replacing lazy deletion
You are given an array of length n. Answer to m query of types:
- “What is the maximum element in interval [x,y] ? ”.
- The elements on positions [x,y] take the value z.
The only thing we must keep in addition is a variable ff that works as follows:
- if
ff != 0then the maximum will be fixed - if
ff == 0then we have to compute the maximum
It works just as lazy deletion on segment trees. That is, if we need to look for a value inside a k-segment then is the segment is fixed we update all it's elements with ff. If we need to compute the maximum on a fixed segment is not necessary to go inside it, but rather just respond with value ff. Complexity will be O(N+M sqrt N).
Why the k-segment notation ?
Sometimes taking K=sqrt(N) isn't the best idea. It was the case the following problem form National Olympics in Informatics Romania.
We have a vector v with n elements and a number m. The vector has to be split in exactly m continuous subsequences such that each element has to be in one subsequence. We define the control value of some subsequence as [(maximum-minimum+1)/2]. We have to split the array such that the maximum control value of each subsequence will be as small as possible. ( n <= 1,000,000 and m <= 1000 )
For example if we split the array [13,4,6,19,4,10] in [13,4,6] , [19] , [4,10] we have the control values 5,0,3 so the answer will be 5.
Firstly , let's solve the problem in a not-so-good complexity. We binary search the result, making a greedy verification function. As long as one can expand the current continuous sequence to the right side ( i.e. [(maximum-minimum+1)/2] <= binary_searched_value ) , we move to the right. If we can split the array in m or less sequences, the verification function will return true. The complexity will be O(N log max_ans).
Now we have to improve the complexity of some verification. We split the array in k-sequences ( of length k ). For each sequence keep maximum and minimum. Now, instead of trying to add only one value to the sequence we can try to add k values to it. This will give us the complexity O(N/K+M*K) per verification as we have maximum N/K “full” k-segments to be added and we start to add a new continuous segment to the solution at most M times.
The only thing lest to do it to choose K. If we choose K = sqrt(N) ( <= M ), this will give no improvement. But if we choose K as 100 , this will make our algorithm significantly faster. Final complexity will be O(N + (N/K+M*K) log max_ans).
The stick fighter
Now we're talking business, right ?
You are given a conex graph with n nodes and m edges. You are given q queries of the type k , a[1] , a[2] … a[k] ( 1 <= a[i] <= m ) and you have to find out for each query if the graph is conex after eliminating edges with indexes a[1] , a[2] … a[k]. Note that each query is independent. ( q*k , m <= 100,000 )
The solution that uses sqrt decomposition splits the queries in groups of k = sqrt(q). Now let's solve the problem for each group of queries.
nbr = int(sqrt(q));
for (int i=1;i<=q;++i)
{
bunch.push_back(i);
if ( int(bunch.size()) == nbr )
{
solve(bunch);
bunch.clear();
}
}
if ( bunch.size() )
solve(bunch);
First of all , let's compress all the nodes that we are not interested in. That is we keep all edges instead of edges in all queries in the current bunch and make a new node for each conex component in this graph. The new graph will have only nodes and no edges.
Let's compute the answer for each query in our bunch. For a query we will add edges in the new graph. Each added edge has a corresponding edge in the old graph. The edges in the old graph that I referred to are all groups of edges for all other k-1 queries.
The complexity will be O(N+sqrt(Q)*K) per bunch. In total the complexity will be O(sqrt(Q) * (N+sqrt(Q)*K)) = O(N*sqrt(Q)+Q*K).
To be sure you understood, let's take a quick example. In the picture the edges marked with red are the first query and the ones with blue are the second one. Suppose we make a bunch out of queries 1 and 2.
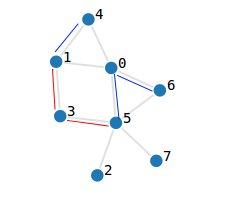
The new graph will be made out of nodes 0' = [0,1,4] , 1' = [3] , 2' = [2,5,6,7]. When we solve query one, edges (1,4) , (0,5) , (0,6) will be added, so in the new graph we will have an edge added between 0' and 2' , therefore the new graph will not be conex. When we solve query two, edges (1,3) , (3,5) are added, so (0',1') and (1',2') are added in the new graph, therefore the new graph will be conex.
You can find a similar problem here .
On CodeForces
PS
Even if I initially planned to include one more problem, I wanted to finish the article before moving to London, so here it is. ( I might do that if I have enough time next month ) The next tutorial will probably come in the second half of October.
Please state your opinion on my tutorial. ( or, more specifically, on my writing style and how useful you find the material presented ) Also, if you have any suggestions on what the next tutorial should be on, feel free to comment. Moreover, if you demand a more specific topic is much likely I would choose it before a larger topic. ( e.g. segment trees would be more likely then data structures )
The possible mistakes will be fixed on Tuesday. You can find my previous article here.
Hope you enjoyed!










Auto comment: topic has been updated by DanAlex (previous revision, new revision, compare).
thanks for another great article.
The blog post is great, but I'm having some trouble understanding the solution to the stick fighter problem. I think it might be flawed.
For example, take exactly the graph you have taken and swap the two queries. Now, using your idea, if we solve the query, it will answer NO. Whereas it is supposed to be YES.
More formally, for a query block query{[0-5], [1-6], [1-4]} and query{[1-3], [3-5]}, answer for query 1 should be YES and query 2 should be NO, but the idea you have appears to give NO for query 1.