Problem A
It is a necessary and sufficient condition that we have exactly 2 distinct values for x and y. If we have less than 2 distinct values for any variable, then there is no way to know the length of that dimension. If there are at least 3 distinct values for any variable, then that means more than 3 vertices lie on that dimension, which cannot happen since there can be at most 2 vertices in a line segment. The area, if it can be found, is just the difference of values of the x coordinates times the difference of values of the y coordinates.
Complexity: O(1)
Code: Solution
Problem B
No matter what, we make |b1| operations to make a1 equal to b1. Once this is done, a2, a3, ... an = b1. Then no matter what, we must make |b2 - b1| operations to make a2 equal to b2. In general, to make ai = bi we need to make |bi - bi - 1| operations, so in total we make |b1| + |b2 - b1| + |b3 - b2| + ... + |bn - bn - 1| operations.
Complexity: O(n)
Code: Solution
Problem C
Note that if there is an integer d so that the number of wi equal to d differs from the number of the given squares whose weight equals d, then the answer is automatically "NO". This can be easily checked by using a map for the wi and the weights of the squares and checking if the maps are the same. This step takes 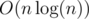 time.
time.
Let d be an integer, and let D be the set of all i so that wi = d. Let W be the set of all special points (x, y) so that the weight of (x, y) is d. Note that W and D have the same number of elements. Suppose that i1 < i2 < ... < ik are the elements of D. Let (a, b) < (c, d) if a < c or a = c and b < d. Suppose that (x1, y1) < (x2, y2) < ... < (xk, yk) are the elements of W. Note that the point (xj, yj) has to be labeled by ij for 1 ≤ j ≤ k.
Now, each special point is labeled. It remains to check if this is a valid labeling. This can be done by taking an array of vectors. The vector arr[i] will denote the points with x-coordinate i. This vector can be easily made from the points given in O(n) time, and since the points are already labeled, arr[i][j] will denote the label for the point (i, j). Now, for all points (i, j), the point (i, j + 1) (if it is special) and the point (i + 1, j) (if it is special) must have a greater number than (i, j). This step takes a total of O(n) time.
Complexity: 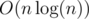
Code: Solution
Bonus: Can you do this problem in O(n) time?
Comments: This problem was inspired by the representation theory of the group of permutations Sn (Representation theory of the Symmetric Group). Essential objects in the study of Sn are Young diagrams and standard Young tableau (Young Tableau). The weight of a point as defined by the problem is basically the same thing as the content of a square in a standard Young tableaux. If you have questions, feel free to message me.
Problem D
Let us solve this problem using dynamic programming.
First let us reindex the trees by sorting them by x-coordinate. Let f(i, j, b1, b2) where we would like to consider the problem of if we only have trees i... j standing where b1 = 1 indicates that tree i - 1 falls right and b1 = 0 if it falls left and b2 = 1 indicates that tree j + 1 falls right and b2 = 0 if it falls left.
We start with the case that Wilbur chooses the left tree and it falls right. The plan is to calculate the expected length in this scenario and multiply by the chance of this case occurring, which is 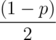 . We can easily calculate what is the farthest right tree that falls as a result of this and call it wi.
. We can easily calculate what is the farthest right tree that falls as a result of this and call it wi.
Then if wi > = j this means the entire segment falls, from which the length of the ground covered by trees in i... j can be calculated. However, be careful when b2 = 0, as there may be overlapping covered regions when the tree j falls right but the tree j + 1 falls left.
If only wi < j, then we just consider adding the length of ground covered by trees i... wi falling right and add to the value of the subproblem f(wi + 1, j, 1, b2).
There is another interesting case where Wilbur chooses the left tree and it falls left. In this case we calculate the expected length and multiply by the chance of this occurring, which is 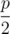 . The expected length of ground covered by the trees here is just the length contributed by tree i falling left, which we must be careful calculating as there might be overlapping covered regions with the ith tree falling left and the i - 1th tree falling right. Then we also add the value of subproblem f(i + 1, j, 0, b2).
. The expected length of ground covered by the trees here is just the length contributed by tree i falling left, which we must be careful calculating as there might be overlapping covered regions with the ith tree falling left and the i - 1th tree falling right. Then we also add the value of subproblem f(i + 1, j, 0, b2).
Doing this naively would take O(n3) time, but this can be lowered to O(n2) by precalculating what happens when tree i falls left or right.
We should also consider the cases that Wilbur chooses the right tree, but these cases are analogous by symmetry.
Complexity: O(n2)
Code: Solution
Problem E
Solution 1: Suppose that s is a string in the query. Reverse s and the direction of all the moves that can be made on the table. Note that starting at any point that is part of a cycle, there is a loop and then edges that go out of the loop. So, for every point, it can be checked by dfs whether the s can be made by starting at that point by storing what is in the cycle.
Moreover, note that in the reversed graph, each point can only be a part of one cycle. Therefore, the total time for the dfs in a query is O(nm·SIGMA + |s|). This is good enough for q queries to run in time.
Complexity: 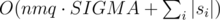 where SIGMA = 10 is the number of distinct characters in the table, and si is the query string for the i th query.
where SIGMA = 10 is the number of distinct characters in the table, and si is the query string for the i th query.
Code: Solution
Solution 2 (Actually too slow, see comment by waterfalls below for more details): For each string s, dfs from every node that has in degree equal to 0 in the original graph. There will be a path which leads into a cycle after which anything in the cycle can be used any number of times in s. Only every node with in degree equal to 0 has to be checked because every path which leads to a cycle is part of a larger path which starts with a vertex of in degree 0 that leads into a cycle.
This solution is slower, but it works in practice since it is really hard for a string to match so many times in the table. Each query will take O(n2·m2 + si) time, but it is much faster in practice.
Complexity:  where SIGMA = 10 is the number of distinct characters in the table, and si is the query string of the i th query.
where SIGMA = 10 is the number of distinct characters in the table, and si is the query string of the i th query.










Fast editorial!
Editorial was published before contest end.
It wasn't publish, it was saved as draft.
Great work :)
can someone plz explain problem statement of C..
my code
Please, take a look.
There's a typo I think in E's part,
should be
am I rigt? Anyway thanks for very-very fast editorial :) A good practice it is.
Yeah. I saw that and fixed it.
Bonus: Can you do this problem in O(n) time?Yes, yes I do :)
http://codeforces.com/contest/596/submission/14283371
omg o_O 363 lines
Well, the solution is only in the method solve() which is only 57 lines :)
14282779 is mine O(n) solution. It's a bit shorter. :)
How can the obtained labelling in Problem C be checked in O(n) time? (in O(nlogn) solution)
check out my solution 14282779
Updated the editorial.
We can do this without sorting. Observe that we can greedily place a certain w[i] to the "earliest slot" in a diagonal (y — x).
There are only 200000 diagonals of the form y — x, so we can just store these "earliest slots" in an array. We can use either x-coordinate or y-coordinate to represent the earliest slot, and just use the fact that w = y — x to get the other coordinate.
Therefore, to do this in O(n), just iterate array w, and if the earliest possible slot in the diagonal w[i] is available (i.e. its left and bottom adjacent positions are already filled), then we can proceed to fill the others. Otherwise, if the slot is not a valid point or its adjacents are not yet filled, there is no more solution and we print "NO".
Here's my solution :)
I solved D problem at the end of contest. i forgot x == y , the left index == the right index. I am so sad.
Test 76 on C is a winner. Who's idea was to add it?
:( For 0,0 I've put position 1 instead of the first position in array w of 0...
Could be someone's great hack added later to the main suit. Killed my solution for C :(
When we can see results?
Results have been posted on blog
For Problem B you can simulate the operations optimally using a BIT and you get a O(n * log(n)) time complexity. Here is my solution http://codeforces.com/contest/596/submission/14287599. (Unfortunately I didn't manage to get Accepted during contest due to integer overflow.)
O(n) faster
'Now, each special point is labeled. It remains to check if this is a valid labeling, which can easily be done in O(n) time.' — Can someone explane me checking it in O(n)? My solution consists BIT — O(n log n).
I will update this soon.
Thanks. The tasks were great and interesting to me. Only I expected a little easier third and fourth, but this is also ok :)
Updated the editorial.
,
I think the second solution to E is too slow. I don't think "it works in practice since it is really hard for a string to match so many times in the table" really matters, since we can just make all queries a single character that doesn't appear in the table at all (it then looks through the whole path). If there are a lot of degree 0 nodes (even O(n)), the complexity can be O(n2mq) which shouldn't work for n = m = q = 200.
For example see this test: http://pastebin.com/qbRypHZC (basically a winding path with inputs in the first and last column).
Wow. Well, I stand corrected.
For Problem C:
This
nlognsolution gots TLE, why ?solution: 14286507
The
lower_boundfunction on sets takes O(n) time. You should dos.lower_bound(something)which takes O(log(n)) time notlower_bound(all(s),something)which would take O(n) time.First time to know this, thank you :)
It was also possible to do C with a 2D binary indexed tree, by only allocating memory for parts of the tree that were nonzero. It took O(nlog^2 n) time, and the same amount of memory. It just barely fits in the time limit though. Here is the code.
Here's another idea for E. For each vertex in the graph, build jump hashes in powers of two. Then for any query, we can binary search from each vertex to see if the query string matches. The complexity should be something like O(qn2log(Σi|si|)).
This is an interesting idea. Thanks for sharing that!
In problem C solution, I have problem in this part of the code. for (int i=0; i<n; i++) { int a, b; scanf("%d %d",&a,&b); while (diag[a].size()<=b) diag[a].push_back(0); weights[b-a].push_back(make_pair(a,b)); } Shouldn't the complexity of this code due to the while loop make it O(MAX_X *MAX_Y) where MAX_X=MAX_Y=100000.
No, it doesn't become like this because each point is added exactly once making a total of n points.
May I ask what is meaning of some variable in solution of Problem D? like
int sz[2][MAX_N];, I guess it used to save the preprocess value of sth , but i couldn't understand how it use.int nl=min(rig,lef+sz[0][lef]-1);, I also don't understand what's nl meansorry for my poor English
So, the
szarray is used to store the preprocessing. The valuesz[0][i]says how many trees fall down if the i th tree falls down. The valuesz[1][i]is the same thing if the i th tree falls right. The variablesnlandnrare for the last tree that falls if theleffalls right and the last tree that falls ifrigfalls left, respectively. Note that these are bounded byrigandlef, respectively. So, you have to take the minimums.In problem C, many submissions cannot pass this test case: 5 0 0 0 1 0 2 1 0 1 1 0 1 0 2 -1
It should be "NO", right?
in solution C, isn'it TLE when inputs are 100000 1 100000 2 100000 3 100000 .... 100000 100000 ....
while (diag[a].size()<=b) diag[a].push_back(0); because of this line?
Read the problem carefully again: Also, it is guaranteed that if some point (x, y) is present in the input, then all points (x', y'), such that 0 ≤ x' ≤ x and 0 ≤ y' ≤ y, are also present in the input. So the test you constructed is invalid.
Also read this comment.
Thanks for your explanation :)
can somebody explain problem E editorial