I was trying 484E - Sign on Fence. Here are my two submissions:
The only thing I changed in these two submissions is in the update method. Instead of having
int k = update(L[ID], low, mid, qx);
L[ID] = k;
I put
L[ID] = update(L[ID], low, mid, qx);
and the same thing with the array R. This should work the same way, but one gives Accepted and the other gives WA. Is there any specific reason why this happens?








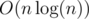 time.
time.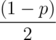 . We can easily calculate what is the farthest right tree that falls as a result of this and call it
. We can easily calculate what is the farthest right tree that falls as a result of this and call it 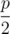 . The expected length of ground covered by the trees here is just the length contributed by tree
. The expected length of ground covered by the trees here is just the length contributed by tree 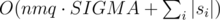 where
where  where
where 
