This is a technical problem. You should do exactly what is written in problem statement.
600B - Queries about less or equal elements
Let's sort all numbers in a. Now let's iterate over elements of b and for element bj find the index of lowest number that is greater than bj. We can do that using binary search. That index will be the answer for value bj.
Complexity: O(nlogn).
Let's denote cntc — the number of occurences of symbol c. Let's consider odd values cntc. Palindrome can not contain more than one symbol c with odd cntc. Let's denote symbols with odd cntc as a1, a2...ak (in alphabetical order). Let's replace any one of symbols ak with symbol a1, ak - 1 with a2 and so on until the middle of a. Now we have no more than one odd symbol. If we have some let's place it in the middle of the answer. First half of answer will contain 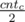 occurences of symbol c in alphabetical order. The second half will contain the same symbols in reverse order. For example for string s = aabcd at first we will replace d by
occurences of symbol c in alphabetical order. The second half will contain the same symbols in reverse order. For example for string s = aabcd at first we will replace d by
Unable to parse markup [type=CF_TEX]
in the middle and after permuting the symbols we got abcba. Easy to see that it's the optimal solution.Compexity: O(n).
600D - Area of Two Circles' Intersection
If the circles don't intersect than the answer is 0. We can check that case with only integer calculations (simply by comparing the square of distance between centers with square of the sum of radiuses). If one of the circles is fully in other then the answer is the square of the smaller one. We can check this case also with only integer calculations (simply by comparing the square of distance between centers with square of the difference of radiuses).
So now let's consider the general case. The answer will be equal to the sum of two circular segments. Let's consider the triangle with apexes in centers if circles and in some intersecting point of the circles. In that triangle we know all three sides so we can compute the angle of the circular segment. So we can compute the square of circular sector. And the only thing that we should do now is to subtract the square of triangle with apexes in the center of circle and in the intersecting points of circles. We can do that by computing the half of absolute value of cross product. So we have the following formulas:
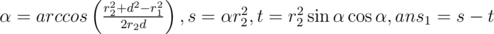 ,
,
where d is the distance between centers of the circles. And also we should do the same thing with second circle by replacing of indices 1 ≤ ftrightarrow2.
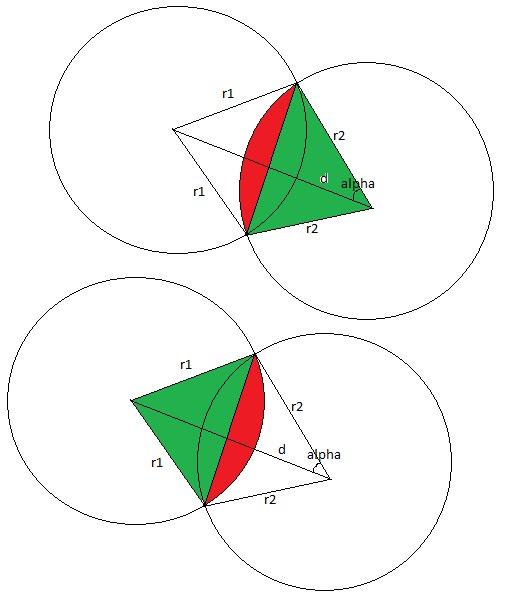
Complexity: O(1).
The name of this problem is anagram for ''Small to large''. There is a reason for that :-) The author solution for this problem uses the classic technique for computing sets in tree. The simple solution is the following: let's find for each vertex v the ''map<int, int>'' — the number of occurences for each colour, ''set<pair<int, int>>'' — pairs the number of occurences and the colour, and the number sum — the sum of most frequent colours in subtree of v. To find that firstly we should find the same thing for all childs of v and then merge them to one. These solution is correct but too slow (it works in O(n2logn) time). Let's improve that solution: every time when we want to merge two map-s a and b let's merge the smaller one to larger simply by iterating over all elements of the smaller one (this is the ``Small to large''). Let's consider some vertex v: every time when vertex v will be moved from one map to another the size of the new map will be at least two times larger. So each vertex can be moved not over than logn times. Each moving can be done in O(logn) time. If we accumulate that values by all vertices then we get the complexity O(nlog2n).
I saw the solutions that differs from author's but this technique can be used in a lot of other problems.
600F - Edge coloring of bipartite graph
Let's denote d is the maximum degree of vertex in graph. Let's prove that the answer is d. We will build the constructive algorithm for that (it will be the solution to problem). Let's colour the edges one by one in some order. Let (x, y) be the current edge. If there exist colour c that is free in vertex x and in vertex y then we can simply colour (x, y) with c. If there is no such colour then there are a couple of colours c1, c2 so that c1 is in x and not in y and c2 is in y but not in x. Let's make vertex y free from colour c2. Denote z the other end of edge from y with colour c2. If z is free from colour c1 then we can colour x, y with c2 and recolour y, z with c1. So me make alternation. If z is not free from colour c1 let's denote w the other end of the edge from z with colour c1. If w is free from colour c2 then again we can do alternation. And so on. We will find an alternating chain because the graph is bipartite. To find the chain we can use depth first search. Each chain contains no more than O(n) vertices. So we have:
Сложность решения: O(nm).











Hi,
Do you have an English translated version of your blog?
Thanks.
I've done the first four problems. Working on the last two.
Fine. I am waiting for it. Eager to know the logic. Thanks. :)
Thank Edvard so much for this editorial!!
How do you ensure that your formulas are precise enough? It is pretty easy to come up with those formulas, however it is much harder to convince yourself (and guys preparing tests) that it will be sufficiently precise on tests like:
As one particular example, the formula found here (equation 13) is not precise enough, at least without BigDecimals, while the editorial's formula works with long double (and some double mixed in).
The only difference between my two submissions 14517685 — WA28 and 14533916 — AC is that the second uses the formula from the editorial, while the first is from the above link.
The two formulas are almost the same, but differ in one part that is subtracted. I think the reason is that the imprecise formula involves taking the square root of a product of four terms, which might compound the error or something. Could someone shed some light on this?
The way to ensure this is to avoid at all costs substration or addition of floating point numbers. If we are adding floating point numbers we'd better ensure they are of the same sign. In other words, stick with ints as long as you can. I saw two problems (not sure if they equally serious):
1) the acos(x) function is flat for x near to 1. So in these cases it would be preferable to determine the angle though asin. It is possible to calculate a precise length of the perpendicular from the circle crossing onto the line connecting the centers. I did it using Heron's formula for area of a triangle. Therefore we can use asin instead of acos.
2) calculating asin(x)-x for small x. I did it using Taylor series around x=0.
Solution: http://pastebin.com/LV5qaK1Q
i calculate sin alpha using the area of the triangle s = 1/2 * (r1 * dis)* sin(alpha) then i calculate s using s = sqrt(p * (p — r1) * (p — r2) * (p — dis)) then i get wrong answer on test 9 !! where dis is the distance between the centers of the circles why this happen?
Auto comment: topic has been updated by Edvard (previous revision, new revision, compare).
Could someone, please, provide a readable piece of code for problem E?
Thanks a lot.
E is such a nice task. It can be solved in n sqrt n (with MO alg), n log^2, n log n with centroids,n log n and even n * DSU :P
I'd like to learn all of these methods. Could you provide some good links for learning?
Thanks!
How do you solve it in nlogn and n*DSU?
N log N with no stl cheats is as follows: We'll use smaller to larger technique, but provide merging with no additional log. We'll maintain a vector for each component (it's like find & union) and support O(1) merging for each element in it. (therefore overall merge for 2 components will bo O(smaller)). Well known fact, subtree query could be changed into some preorder array contiguous segment query. This is not important at all, but we can come up with the idea of faster merging — a vertex of a colour X will always be merged first with the nearest vertex of colour X in preorder array. (Left or right, two cases). So we could preprocess for each colour all occurences of it and merge in O(1). Some additional arrays might be needed, but it's the main idea.
Do you happen to have code for this?
On task E, if our tree is a line of 10^5 nodes and value is different for each node. For every node we store all different colors in subtree of v in map, and in this case we should use N^2 memory, shouldnt we?
No, parent uses map of biggest son.
Is the memory complexity O(n*log(n)) ?
Did you get the answer?
Can anyone please explain the statement Let's replace any one of symbols ak with symbol a1, ak - 1 with a2 and so on until the middle of a. Now we have no more than one odd symbol. with sample string bbbcccddd
Why does my solution for 600A get TLE? http://codeforces.com/submissions/r4huln/
your solution is O(n square) and the input is too big for n square
So how should I solve this more efficiently?
use binary search as written in editorial
Can any one tell me what's the difference between __mingw_printf("%Lf") and cout when printing long double?
Here's my solution:
14537257 __mingw_printf
14536996 cout
which first one got Wrong Answer, and the second one got Accepted.
I'm totally confused.
Thanks a lot.
Hello, I have a question about Problem D. I fail to hack the solution with the Data like this:
The result should be pi*r^2 = pi*1e18 = 3141592653589793238.46264338. The answer should be at least in this interval:
on condition that the absolute error of area doesn't exceed 1e-6. ("The answer will be considered correct if the absolute or relative error doesn't exceed 10 - 6")
That is to say, we should not store pi in 80 or 96 bits long-double variable because we need at least first 24 digits of pi to get correct result for this data. I have checked the output of the code based on long double and confirmed that the absolute error of that solution > 1e-6, but I still got "Unsuccessful hacking attempt". Would you like to tell me the reason?
On the other hand, acosl(-1) = 3.141592653589793238512... here. Only first 19 digits of pi are correct and the absolute error will be about 1 (pi*1e18).
Thanks.
Solution can return result with relative error of 1e-6 rather than absolute error of 1e-6.
Thanks.
will you add codes for problems?
in problem F ..can we extend this solution to general graphs ?
If I am not wrong there is an algorithm to paint in d + 1 colours.
can you provide a link please ?
Sorry, I was thinking about vertex coloring, whereas in this problem you must color edges.
yes i think that should work ! thanks a lot ..but do you have a link for such problem on any online judge ?
Can someone explain Make Palindrome using editorial for the case bbbcccddd
cnt[b] = 3 , cnt[c] = 3 , cnt[d] = 3
all of them are odd so a1=b , a2=c , a3=d
replace one of a3 characters with a1 so cnt[b] = 4 , cnt[d] = 2
cnt[c] will remain odd but it is no matter. we can use one c at middle of palindrome.
so palindrome will be : bbcdcdcbb
My code is giving correct output for all the small test cases yet giving wrong answer on test 7 id: http://codeforces.com/contest/600/submission/14548282 can someone tell me where i am missing. I have tried to implement STL.
Please someone provide me cases .
your code gives wrong answer on these cases:
bluespeckisa
nass
holewhof
indsitmorere
spectfulto
livelikead
ogof
somefunnyredcoders
likexell
osbutt
hesadtruth
isxellos
dontfeelen
oughfu
ntogiveashit
toth
ismotherfucker
bitchandgets
angrywhenthisblues
hitmakesjokesf
orhisdearm
asterxelloss
if you want the correct answers for them see here: http://pastebin.com/ZmaE4npq
Thanks man there was bug in the case where i was handling the even length case. I had always looked at odd cases thinking even case to be perfectly fine but it just came the opposite.
Can anyone explain more clearly why the "Small to large" trick reduce the solution complexity to O(n log n) in problem E? Thanks in advance.
Hello there! I'm having the same question as you. Have you managed to figured it out ? Can you please elaborate ?
Maybe this comment will help.
Where to find theory or some examples related to the small to large technique used in Problem E — Lomsat gelral ?
Read the proof of Union by Rank algorithm: [here](http://www.wikiwand.com/en/Proof_of_O(log*n)_time_complexity_of_union%E2%80%93find)
I'm using binary search (http://ideone.com/P63MMj ) in 600B but still get TLE. Any ideas why?
The problem is in Arrays.sort. It uses quicksort and there are anti-quicksort tests in this problem now.
For Problem E, can anyone explain "Let's consider some vertex v: every time when vertex v will be moved from one map to another the size of the new map will be at least two times larger." ?
In problem E, I understood the technique of Small to Large. But I have one doubt, if all nodes have different colors, won't all the maps take O(n^2) memory?
I guess I just thought of its logn complexity as a black-box. Now on further thinking, I guess when 2 sets of size s1 and s2 are merged to get a new set of size s3, total memory spaced needed along with the space needed for new set is s3 + min(s1, s2). Moreover, s3 < = (s1 + s2).
I didnt get the same thing...
why solutions are not visible of this round?
https://codeforces.com/contest/600/submission/59420840 Plz explain what's wrong?
You have a 2D array which size is N*N, but MAXN = 1e5 => N*N=1e10, but it's too much
Could anyone show me a detailed proof or explaination for the reduction of time complexity in problem E.Lomsat gelral when using smaller to larger technique?
Really appreciate for your help <3. I have been contemplating this for nearly a week and still haven't figured stuff out :<.
You need to consider Heavy Light Decomposition of the tree. Number of ancestors of u that traverse u is equal to number of light edges on path from u to the root which is O(log n). Thus, each node is traversed O(log n) times.
In problem 4, I am getting wrong ans at test case no. 34 and my ans is off by (.02). But I guess that my way evaluating area kite which is (p*q)/2 where (p is diagonal 1 and q is diagonal 2) is more accurate as it involves less rounded off values. Can it happen that my solution is more accurate than a given solution or please correct me if I am doing anything wrong? Below is the link to my submission:- https://codeforces.com/contest/600/submission/79322952
I am also facing the same issue.
why is the memory complexity not O(n^2)?
Like for example if we have n nodes connected in a straight line and each node has color = index,
then on merging ,each time the parent's map will have one more element than the child's map and sum of elements would be like sum = 1 + 2 + 3 .... + n — 1 + n.
can anyone please tell where i am wrong?