710A - Ходы короля
Easy to see that there are only three cases in this problem. If the king is in the corner of the board the answer is 3. If the king is on the border of the board but not in a corner then the answer is 5. Otherwise the answer is 8.
Complexity: O(1).
710B - Оптимальная точка на прямой
The function of the total distance is monotonic between any pair of adjacent points from the input, so the answer is always in some of the given points. We can use that observation to solve the problem by calculating the total distance for each point from the input and finding the optimal point.
The other solution uses the observation that the answer is always is the middle point (by index) in the sorted list of the given points. The last fact is also can be easily proven.
Complexity: O(nlogn).
710C - Магический нечётный квадрат
The problem was suggested by Resul Hangeldiyev Resul.
The solution can be got from the second sample testcase. Easy to see that if we place all odd numbers in the center in form of rhombus we will get a magic square.
Complexity: O(n2).
710D - Две арифметические прогрессии
I wanted to give this problem a lot of time ago. I thought it is very standard problem, but I underestimated its difficulty.
Let's write down the equation describing the problem: a1k + b1 = a2l + b2 → a1k - a2l = b2 - b1. So we have linear Diofant equation with two variables: Ax + By = C, A = a1, B = - a2, C = b2 - b1. The solution has the form: 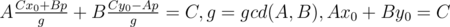 , where the last equation can be solved by extended Euclid algorithm and p is any integral number. The variable p should satisfy two conditions:
, where the last equation can be solved by extended Euclid algorithm and p is any integral number. The variable p should satisfy two conditions: 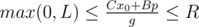 and
and 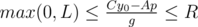 . The values A and B are fixed, so we can get the segment of possible values for the values p. The length of the segment is the answer for the problem.
. The values A and B are fixed, so we can get the segment of possible values for the values p. The length of the segment is the answer for the problem.
Complexity: O(log(max(a1, a2))).
710E - Генерация строки
The problem was suggested by Zi Song Yeoh zscoder.
This problem has a simple solution described by participants in the comments.
My solution is a little harder. Let's solve it using dynamic programming. Let zn be the smallest amount of time needed to get n letters 'a'. Let's consider transitions: the transition for adding one letter 'a' can be simply done. Let's process transitions for multiplying by two and subtraction by one simultaneously: let's decrease the number 2·i i times by one right after getting it. Easy to see that such updates never include each other, so we can store them in queue by adding the new update at the tail of the queue and taking the best update from the head.
The solution is hard to describe, but it is very simple in the code, so please check it to understand the idea :-)
Complexity: O(n).
710F - Операции над множеством строк
The problem was suggested by Alexandr Kulkov adamant.
Let's get rid of the queries for deleting a string. There are no strings that will be added two times, so we can calculate the answer for the added (but not deleted strings) and for the deleted separately and subtract the second from the first to get the answer. So we can consider that there are no queries of deletion.
Now let's use Aho-Corasik algorithm. The only difficulty is that the strings are adding in online mode, but Aho-Corasik algorithm works only after adding all the strings. Note that the answer for the given set of strings equal to the answer for any part of the set plus the answer for the remaining part. Let's use the trick with converting the static data structure (Aho-Corasik in this case) to the dynamic one.
For the set of n strings let's maintain a set of no more than logn sets of the strings with sizes of different powers of two. After adding new string we should move the sets from the lowest powers of two to the largest until we got an invariant set of sets.
Easy to see that each string will be moved no more than logm times, so we can process each query in O(logn) time.
Complexity: O((slen + m)logm), where slen is the total length of the string from the input.










 contains the number of ones in binary presentation that is multiple of three. Otherwise let
contains the number of ones in binary presentation that is multiple of three. Otherwise let 
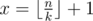 . To learn more about floor/ceil functions I reccomend the book of authors Graham, Knuth, Patashnik "Concrete Mathematics". There is a chapter there about that functions and their properties.
. To learn more about floor/ceil functions I reccomend the book of authors Graham, Knuth, Patashnik "Concrete Mathematics". There is a chapter there about that functions and their properties. .
.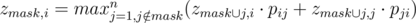 .
.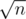 blocks. Consider the lines added before the current block and that will not deleted in the current block. Let's build the lower envelope by that lines. Now to calculate the answer to the query we should get maximum over the lines from the envelope and the lines from the block before the current query that is not deleted yet. There are no more than
blocks. Consider the lines added before the current block and that will not deleted in the current block. Let's build the lower envelope by that lines. Now to calculate the answer to the query we should get maximum over the lines from the envelope and the lines from the block before the current query that is not deleted yet. There are no more than 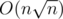 .
.

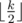 characters in the segment to remove all the pairs of equal consecutive letters. On the other hand we can simply change the second, the fourth etc. symbols to letter that is not equal to the letters before and after the segment.
characters in the segment to remove all the pairs of equal consecutive letters. On the other hand we can simply change the second, the fourth etc. symbols to letter that is not equal to the letters before and after the segment. is used for the binary operation for bitwise exclusive or.
is used for the binary operation for bitwise exclusive or.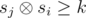 . Let's iterate over
. Let's iterate over 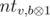 , because all the leaves in the subtree of tha vertex correspond to the values
, because all the leaves in the subtree of tha vertex correspond to the values  and recalculate the value
and recalculate the value 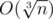 , where
, where 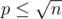 . So for fixed
. So for fixed 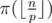 .
. , for all
, for all  . Then
. Then  values of
values of 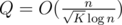 .
.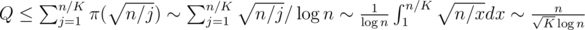
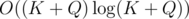 , and it is the heaviest part of the computation. Choosing optimal
, and it is the heaviest part of the computation. Choosing optimal 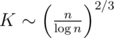 , we obtain the complexity
, we obtain the complexity 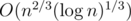 .
.
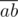 :
: 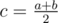 . Let's calculate the value
. Let's calculate the value  .
.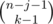 choices to do that (it's simply binomial coefficient with allowed repititions). The number of sequences
choices to do that (it's simply binomial coefficient with allowed repititions). The number of sequences  . Easy to transform the last sum to the sum
. Easy to transform the last sum to the sum 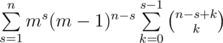 . Note the last inner sum can be calculating using the formula for parallel summing:
. Note the last inner sum can be calculating using the formula for parallel summing: 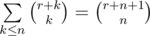 . So the answer equals to
. So the answer equals to 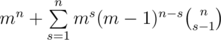 . Also we can get the closed formula for the last sum to get logarithmic solution, but it is not required in the problem.
. Also we can get the closed formula for the last sum to get logarithmic solution, but it is not required in the problem.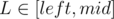 ,
, 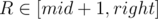 ) we will try to write the score of interval
) we will try to write the score of interval 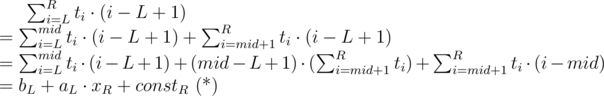
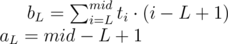
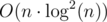 because we sort by
because we sort by 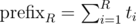 in advance because it's equivalent to sorting by
in advance because it's equivalent to sorting by  is possible this way — anybody implemented it?
is possible this way — anybody implemented it?
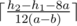 .
.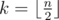 be the number of even positions in
be the number of even positions in 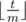 times.
times.
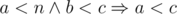 ). Consider an optimal answer with two strings in reverse order by that operator. Because of the transitivity of operator we can assume that pair of strings are neighbouring. But then we can swap them and get the better answer.
). Consider an optimal answer with two strings in reverse order by that operator. Because of the transitivity of operator we can assume that pair of strings are neighbouring. But then we can swap them and get the better answer.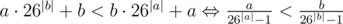 . The last is simply the relation between real numbers. So we proved the transitivity of the relation
. The last is simply the relation between real numbers. So we proved the transitivity of the relation 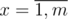 and
and 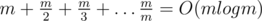 .
.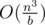 , where
, where 
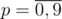 in position
in position 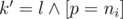 . To update the next state we should increase it:
. To update the next state we should increase it: 
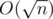 .
.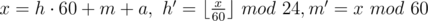 .
.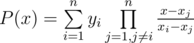 . In our case
. In our case 
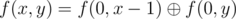 . The values
. The values 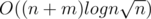 .
.
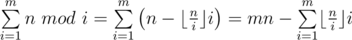 . Note that the last sum can be accumulated to only value
. Note that the last sum can be accumulated to only value 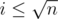 or
or  . Let's carefully accumulate both cases. The first sum can be simply calculated by iterating over all
. Let's carefully accumulate both cases. The first sum can be simply calculated by iterating over all 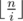 . Firstly we should determine for which values
. Firstly we should determine for which values 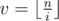 . Easy to see that for the values
. Easy to see that for the values 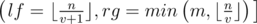 . Also we can note that the sum of the second factors in
. Also we can note that the sum of the second factors in 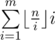 with fixed first factor can be calculaed in constant time — it's simply a sum of arithmetic progression
with fixed first factor can be calculaed in constant time — it's simply a sum of arithmetic progression  . So we have solution with complexity
. So we have solution with complexity 
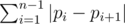 .
.
