622A - Infinite Sequence
Let's decrease n by one. Now let's determine the block with the n-th number. To do that let's at first subtract 1 from n, then subtract 2, then subtract 3 and so on until we got negative n. The number of subtractions will be the number of the block and the position in the block will be the last nonnegative number we will get.
Complexity: 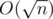 .
.
622B - The Time
In this problem we can simply increase a times the current time by one minute (after each increasing we should check the hours and the minutes for overflow).
Another solution is to use the next formulas as the answer: 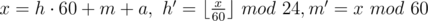 .
.
Complexity: O(a) or O(1).
622C - Not Equal on a Segment
This problem is a simplified version of the problem suggested by Mohammad Nematollahi Deemo.
This problem can be solved differently. For example you can use some data structures or sqrt-decomposition technique. But it is not required. We expected the following simple solution from the participants. Let's preprocess the following values pi — the position of the first element to the left from the i-th element such that ai ≠ api. Now to answer to the query we should check if ar ≠ x then we have the answer. Otherwise we should check the position pr.
Complexity: O(n).
622D - Optimal Number Permutation
This problem was suggested by Aleksa Plavsic allllekssssa.
Let's build the answer with the sum equal to zero. Let n be even. Let's place odd numbers in the first half of the array: the number 1 in the positions 1 and n, the number 3 in the positions 2 and n - 1 and so on. Similarly let's place even numbers in the second half: the number 2 in the position n + 1 and 2n - 1, the number 4 in the positions n + 2 and 2n - 2 and so on. We can place the number n in the leftover positions. We can build the answer for odd n in a similar way.
Easy to see that our construction will give zero sum.
Complexity: O(n).
622E - Ants in Leaves
This problem was suggested by Aleksa Plavsic allllekssssa.
Easy to see that the answer is equal to the answer over all sons of the root plus one. Now let's solve the problem independently for each son v of the root. Let z be the array of the depths of all leaves in the subtree of the vertex v. Let's sort z. Statement 1: it's profitable to lift the leaves in order of their appearing in z. Statement 2: denote ax — the time of appearing the x-th leaf in the vertex v, let's consider the leaves zi and zi + 1 then azi + 1 ≥ azi + 1. Statement 3: azi + 1 = max(dzi + 1, azi + 1), where dx is the depth of the x-th leaf in the subtree of the vertex v. The last statement gives us the solution for the problem: we should simply iterate over z from left to right and recalculate the array a by formula from the third statement. All statements can be easily proved and it's recommended to do by yourself to understand better the idea of the solution.
Complexity: O(nlogn).
622F - The Sum of the k-th Powers
This problem was suggested by Ivan Popovich NVAL.
Statement: the function of the sum is a polynomial of degree k + 1 over variable n. This statement can be proved by induction (to make step you should take the derivative).
Denote Px the value of the sum for n = x. We can easily calculate the values of Px for x from 0 to k + 1 in O(klogk) time. If n < k + 2 then we already have the answer. Otherwise let's use Lagrange polynomial to get the value of the sum for the given value n.
The Largange polynomial have the following form: 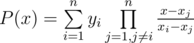 . In our case xi = i - 1 and yi = Pxi.
. In our case xi = i - 1 and yi = Pxi.
To calculate P(n) in a linear time we should use that xi + 1 - xi = xj + 1 - xj for all i, j < n. It's help us because with that property we can recalculate the inner product for i + 1 from the inner product for i simply by multiplying by two values and dividing by two values. So we can calculate the sum in linear time over k.
Complexity: O(klog MOD) (logk appeared because we should find the inverse element in the field modulo MOD = 109 + 7).











very interesting round .. thanks a lot .. waiting for problem E
Done. F is left.
Thanks! I've learned a lot!
Could someone help me with further optimization of my code for prob-c: not equal on segment It is giving tle on test-case 20.
`#include<bits/stdc++.h>
using namespace std;
int main() {
long long int n, m, l, r, x;
long long int a[n], first_on_left[n];
} `
Replace endl with "\n".
use scanf instead of cin. I got tle with cin several times.
The answer to the Infinite Sequence may be done in O(1). We may organize the sequence as: 1 (1) // That means the positions that the first one in that line is 1,2 (2) 1,2,3 (4) 1,2,3,4 (7) 1,2,3,4,5 (11) Then we would have a new sequence, which is much easier to find. 1 (1) 2 (2) 4 (3) 7 (4) 11 The number in the parenthesis are the distance between the number of the new sequence.
To find the base of the number we need to solve the equation x = n(n+1)/2 + 1. Where x is the number we receive as input. We need to isolate n (get the max floor value).
Then we use the n we got in the same formula, but now the result is going to be the base for the line. We only need to calculate the distance between the number we receive as input and the number we got as base.
x — base + 1
SOLUTION: 15944155
Actually A can be done in O(1).
We wanted to make the problem simple, so we gave it with the constraints for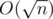 solution.
solution.
as it turns out, A can be done in O(n) if you dare. My O(n) solution in C# + LINQ : 15953718
plz tell me how ?
Let's analyse how long it takes for the sequence to enter a new cycle:
C1=1 : 1
C2=1 2 : (from until here)1+2=3
C3=1 2 3 : (from until here)3+3=1+2+3=6
Ci=1 2 ... i : SUM from 1 to i = (i+1)(i)/2
So if we solve the equation (i+1)*(i)/2=n and get the floor of the positive root we can find in which cycle Ci the answer will come from.
Now you need to know how many numbers were used in the cycle.
(i+1)*(i)/2 is the quantity of numbers used to get past the cycle Ci.
If that result is equal to n, we know that the last number of the sequence is the answer so we print i. Else, i is the cycle right before the one the answer will come from, so we print n-(i+1)(i)/2 (the quantity of numbers used since the end of the last sequence)
Why my code for porb D 15942394 TLE?
I hope for some explanations from more experienced guys, but this code doesn't get TLE in Delphi 7. 15952130
Delphi 7 = FPC ??
Of course, not. They are two different compillers for two different languages. And your code works in D7 ~10 times faster, than in FPC.
thank
I don't know why, but it seems that the output buffer is not fast enough in fpc.
I made a little change: instead of using write() directly,save the things you want to output into a string, and finally writeln(the_string); and this way it passed all the test cases.
16055326
Actually we need O(k ln k) here due to calculating k-th power of each number.
Of course you are right. Fixed.
We can also do it in $$$O(k)$$$. Using linear-time sieve we can express each $$$i \leq k+1$$$ as $$$i = p \cdot j$$$ where $$$j<i$$$ and $$$p$$$ is prime. Then $$$i^k = p^k \cdot j^k$$$, so we only need to calculate the $$$k$$$-th powers for prime numbers up to $$$k+1$$$ and there are only $$$O(\frac{k}{\log k})$$$ of them.
As Far As I Know This Sequence "1, 1, 2, 1, 2, 3, 1, 2, 3, 4, 1, 2, 3, 4, 5...." Is Called "Doubly Fractal Sequence"
I Appl!ed Direct Formula :) ..
My Solution Was : http://ideone.com/NgIE6c
During contest in problem C, I used segment trees to solve. Got Time Limit Exceeded on 19th test case. Only problem was cin,cout. I should have used scanf and printf.
Those interested in segment tree solution of problem C :- http://codeforces.com/contest/622/submission/15960458
Did anyone solve D without writing brute force first? if yes then how did you think until you arrived to the solution?
allllekssssa sent me that problem and I solved it without brute force)
The only hard part in this problem is to predict that zero sum is achievable. After that it's nearly trivial to invent needed permutation.
I agree with you.
And I agree with both :)
I did that.
wrote a brute force first (for a given n, gives out all the possible permuations which have smallest sum).As it turns out:
the minimun sum is always 0.
too many possible sequences.
since it's a constructive problem, we want to find a simple sequence following some patterns.
Let's make some assumptions on possible sequence: there's always a required sequence, which 1 is the first one, and n is always the last one,(you can add more assumptions, since there are too many legal ones) which will lead to a very limited number of sequences. And a beautiful 1 3 5 7 ... 5 3 1 ... n may catch your eye, and now you can build one.
Why does this gives TLE? I think the complexity is O(n) which should satisfy the limits.
Don't mix cin/cout and scanf/printf. It's almost always bad idea. In that exact problem one definitely need to use scanf/printf due to big input.
15964463 (only difference is queries input)
Thanks a lot. Can you explain a bit more why was it giving TLE just because of input functions?
Maximal input size in the problem C is equal to
2*10^5 * 4 * 6 = 4.8 * 10^6characters, because there are2*10^5 * 4numbers and each one can be represented by 6 digits. Reading is a pretty slow operation, requiring approximately O(10) for each digit of a number, and it's particularly slow with built-in cin/cout streams. Cin/cout use various adjustments to make them more useful, e.g. there is a synchronization with scanf/printf which can sometimes come in handy, but it makes them extremely slow too. You'd want to turn it off, as it makes cin/cout much faster. Check out my codes, if you needAnyone solved C with plain binary search?
I wrote segment tree+binary search.
Pure binary search: 15971282
binary search , which has a binary search inside (Complexity: O(mlog2n))
My solution (in C# ):15936162
E is a very good problem :) I liked thinking the editorial solution.
Can anyone explain solution to problem F? I cant get the editorial.
P622C — Doing in O(n) but still getting TLE.
import java.util.Scanner;
Ok same code and I just changed cin cout with printf and scanf and now it's accepted. Can anybody explain this ?
http://codeforces.com/contest/622/submission/16016197
cout << endl flushes the output, use cout << "\n" instead.
Default setting of cin/cout is dramatically slow with such a huge input and output file.
Typically, there are three ways to fix it.
use scanf/printf instead
add std::ios::sync_with_stdio(false); at the very beginning of your main()
write fast I/O methods by your own.
Could anyone tell me more about problem F? I can't understand how we use Lagrange polynomial to solve that problem. Thanks in advance!
How can I optimize this O(n) Haskell solution to C so that it doesn't TLE? Or is it just a limitation of the language?
("build" preprocesses the values of p as described in the editorial. "solve" simply answers the queries using the array we built earlier.)
Can problem E be solved by dp on trees?
Problem C has a very elegant solution posted in the editorial, but just for the sake of learning, can someone tell me how to do it with square root decomposition ?