This round was unusual: some of problems was prepared by students and employees of Saratov State U for some of past olympiads and one of problems was prepared by dalex for Codeforces regular round but was not used there.
Let's sort the array in nonincreasing order. Now the answer is some of the first flash-drives. Let's iterate over array from left to right until the moment when we will have the sum at least m. The number of elements we took is the answer to the problem.
Complexity: O(nlogn).
Let's denote cnti — the number of books of i th genre. The answer to problem is equals to 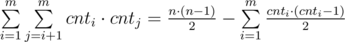 . In first sum we are calculating the number of good pairs, while in second we are subtracting the number of bad pairs from the number of all pairs.
. In first sum we are calculating the number of good pairs, while in second we are subtracting the number of bad pairs from the number of all pairs.
Complexity: O(n + m2) or O(n + m).
Denote s — the sum of elements in array. If s is divisible by n then the balanced array consists of n elements  . In this case the difference between maximal and minimal elements is 0. Easy to see that in any other case the answer is greater than 0. On the other hand the array consists of
. In this case the difference between maximal and minimal elements is 0. Easy to see that in any other case the answer is greater than 0. On the other hand the array consists of 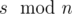 numbers
numbers 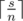 and
and 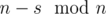 numbers
numbers 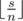 is balanced with the difference equals to 1. Let's denote this balanced array b. To get array b let's sort array a in nonincreasing order and match element ai to element bi. Now we should increase some elements and decrease others. In one operation we can increase some element and decrease another, so the answer is
is balanced with the difference equals to 1. Let's denote this balanced array b. To get array b let's sort array a in nonincreasing order and match element ai to element bi. Now we should increase some elements and decrease others. In one operation we can increase some element and decrease another, so the answer is 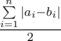 .
.
Complexity: O(nlogn).
609D - Гаджеты за доллары и фунты
If Nura can buy k gadgets in x days then she can do that in x + 1 days. So the function of answer is monotonic. So we can find the minimal day with binary search. Denote lf = 0 — the left bound of binary search and rg = n + 1 — the right one. We will maintain the invariant that in left bound we can't buy k gadgets and in right bound we can do that. Denote function f(d) equals to 1 if we can buy k gadgets in d days and 0 otherwise. As usual in binary search we will choose 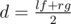 . If f(d) = 1 then we should move the right bound rg = d and the left bound lf = d in other case. If binary search found the value lf = n + 1 then the answer is - 1, otherwise the answer is lf. Before binary search we can create two arrays of gadgets which are selling for dollars and pounds, and sort them. Easy to see that we should buy gadgets for dollars on day i ≤ d when dollar costs as small as possible and j ≤ d when pounds costs as small as possible. Let now we want to buy x gadgets for dollars and k - x gadgets for pounds. Of course we will buy the least cheap of them (we already sort the arrays for that). Let's iterate over x from 0 to k and maintain the sum of gadgets for dollars s1 and the sum of gadgets for pounds s2. For x = 0 we can calculate the sums in O(k). For other x's we can recalculate the sums in O(1) time from the sums for x - 1 by adding gadget for dollars and removing gadget for pounds.
. If f(d) = 1 then we should move the right bound rg = d and the left bound lf = d in other case. If binary search found the value lf = n + 1 then the answer is - 1, otherwise the answer is lf. Before binary search we can create two arrays of gadgets which are selling for dollars and pounds, and sort them. Easy to see that we should buy gadgets for dollars on day i ≤ d when dollar costs as small as possible and j ≤ d when pounds costs as small as possible. Let now we want to buy x gadgets for dollars and k - x gadgets for pounds. Of course we will buy the least cheap of them (we already sort the arrays for that). Let's iterate over x from 0 to k and maintain the sum of gadgets for dollars s1 and the sum of gadgets for pounds s2. For x = 0 we can calculate the sums in O(k). For other x's we can recalculate the sums in O(1) time from the sums for x - 1 by adding gadget for dollars and removing gadget for pounds.
Complexity: O(klogn).
609E - Минимальное остовное дерево по каждому ребру
This problem was prepared by dalex.
Let's build any MST with any fast algorithm (for example with Kruskal's algorithm). For all edges in MST the answer is the weight of the MST. Let's consider any other edge (x, y). There is exactly one path between x and y in the MST. Let's remove mostly heavy edge on this path and add edge (x, y). Resulting tree is the MST contaning edge (x, y) (this can be proven by Tarjan criterion).
Let's fix some root in the MST (for example the vertex 1). To find the most heavy edge on the path from x to y we can firstly find the heaviest edge on the path from x to l = lca(x, y) and then on the path from y to l, where l is the lowest common ancestor of vertices x and y. To find l we can use binary lifting method. During calculation of l we also can maintain the weight of the heaviest edge.
Of course this problem also can be solved with difficult data structures, for example with Heavy-light decomposition method or with Linkcut trees.
Complexity: O(mlogn).
It's very strange but I can't find any articles with Tarjan criterion on English (although there are articles on Russian), so here it is:
Some spanning tree is minimal if and only if the weight of any other edge (x, y) (not from spanning tree) is not less than the weight of the heaviest edge on the path from x to y in spanning tree.
Let's maintain the set of not eaten mosquitoes (for example with set in C++ or with TreeSet in Java) and process mosquitoes in order of their landing. Also we will maintain the set of segments (ai, bi), where ai is the position of the i-th frog and bi = ai + li, where li is the current length of the tongue of the i-th frog. Let the current mosquito landed in the position x. Let's choose segment (ai, bi) with minimal ai such that bi ≥ x. If the value ai ≤ x we found the frog that will eat mosquito. Otherwise the current mosquito will not be eaten and we should add it to our set. If the i-th frog will eat mosquito then it's tongue length will be increased by the size of mosquito and we should update segment (ai, bi). After that we should choose the nearest mosquito to the right the from frog and if it's possible eat that mosquito by the i-th frog (this can be done with lower_bound in C++). Possibly we should eat several mosquitoes, so we should repeat this process several times.
Segments (ai, bi) we can store in segment tree by position ai and value bi. Now to find segment we need we can do binary search by the value of ai and check the maximum bi value on the prefix to be at least x. This will work in O(nlog2n) time. We can improve this solution. Let's go down in segment tree in the following manner: if the maximum value bi in the left subtree of segment tree is at least x then we will go to the left, otherwise we will go to the right.
Complexity: O((n + m)log(n + m)).











I hope you liked my problem E. I'll also try to add some new tests tomorrow, if I have time.
This is the comment with its solution: http://codeforces.com/blog/entry/9570#comment-150780.
Was just a lot of copy-pasting for me :)
This E is really nice.
Any hint on solving with Heavy-light decomposition method or Link Cut Trees? Thanks.
My solution :) http://codeforces.com/contest/609/submission/14893860 Sorry for the chinese comment...
In case someone will be interested, recently I posted even shorter HLD implementation: http://codeforces.com/blog/entry/22072
Thanks DaiDaiBear Al.Cash !
Problem C. For those who don't like formulae: let
cnt[i]denote number of servers with load i. Then, thanks to low numbers, there's solution that (almost) faithfully models rebalancing:How could the approach to "USB Flash Drives" be true?
Take this case for example:
a = {6,3,4,2,5}
m = 10
I presume you'll choose {2,3,4} and return 3 when you should actually choose {4,6} and return 2.
Or am I missing something?
Sort the array in non increasing order i.e. decreasing order. So the array will become : 6,5,4,3,2. You will chose 6 and 5(Till the point your sum is at least m).
What about a O(N) and easier solution for problem C? take a look at this: 14895448
Is this solution hack-able?
I have a similar solution. There is no reason to sort the array — when we know the average, it's clear that maximum of required increments/decrements will satisfy the other one and thus it's correct (on the other hand, at least this number must be reasigned).
why are you checking this — "if(sum>(mx*n))mx++;" if you simply just assign mx=mn+1 , it will work fine .
yeah :D . it will.... it was because of my initial implementation where i just calculated sumOf(min(abs(mn-a[i]),abs(a[i]-mx)))/2; which is clearly a wrong solution!!!
i didnt knew where the upvoting tick was.. by mistake i clicked on the downvote one. now i cant change it . i am sorry ! :p
Go to his profile. Click on comments. Upvote any other 2 comments :P
For problem F, I implemented a square-root decomposition algorithm 14900791 but it gets WA on test 5. Does anybody have any idea why it fails? The general algorithm is: sort frogs by start position (increasing order), partition the frogs into size squareroot(n) sections and keep track of the maximum reach of any frog in that section, and when a mosquito lands, iterate through each section until we find that some frog can reach greater or equal to the position of the mosquito and then find the frog which works (this might not always be possible), if the frog is able to eat it then make it eat it, update the section and then try to find any un-eaten mosquitoes for this frog to eat and keep doing this until no more mosquitoes can be eaten, otherwise if the frog was not able to eat the mosquito that just landed then add it to the un-eaten mosquitoes set.
Change set to multiset.
Oh yes, mosquitoes can land at similar positions... thanks for that. Can't believe I spent an hour staring at my code without seeing that!
"To find l we can use binary lifting method. During calculation of l we also can maintain the weight of the heaviest edge" Can someone help me with how to calculate heaviest edge along with calculating lca? code...? and also can someone explain how this can also be solved using dsu? thanks in advance :)
In C how do we know that 2 divides the sum of the differences?
For every operation (moving task from one server to another) there is server where the task is moved onto (gets +1) and one where is moved from (gets -1). Since we are taking absolute value every time, both times we will increase sum by 1. So every operation adds 2 to the sum. Therefore sum is divisible by 2.
Consider the smallest example possible:
2
1 3
Average is (1 + 3) / 2 = 2. One task will be moved from server 2 (gets -1) to server 1 (gets + 1). And for this task you add abs(1 — 2) + abs(3 — 2) = 2 to the total sum.
i am not able to understand the explanation for problem C . can someone help me?
There's also an alternative solution for problem E. Consider the standard Kruskal's algorithm for finding the MST of a graph. Observe that the heaviest edge on the path from x to y in the resulting tree will be the first edge that connects the components containing x and y during the algorithm. Now while adding an edge to the current tree, simply iterate over the nodes from the smaller component and check if their neighbors are in the larger component, and merge the two components afterwards. We can use the standard disjoint set data structure for that purpose, with additionally storing all nodes from each component on a separate vector.
Pretty well solution!!!!
Quite an elegant solution!
This is my code for E. It passed 10 first cases, but time exceeds limit at test case 11. What should i change?
include <bits/stdc++.h>
using namespace std; typedef long long ll; ll n,m; ll u,v,w; ll per[200000+5];
struct p{ ll u; ll v; ll w; ll id; } e[200000+5];
bool cmp(p a,p b){ return a.w<b.w; }
ll find(ll x){ return per[x] == x ? x:find(per[x]); } int main(){ cin>>n>>m; for(int i = 0;i<m;i++){ cin>>u>>v>>w; e[i].u =u; e[i].v = v; e[i].w =w; e[i].id = i; }
}
Your solution very slow, this is O(n * m) time. You need to use fast data structures. My solution with Sparse Table on tree, DSU, MST, in O(n log(n)) time
Can you help me with how to calculate maximum edge weight along a path using sparse table. I know how to get LCA using sparse table. I read your code, couldn't figure out properly.
Update: Got it! Thanks!
98388177
Someone please help with why this code doesn't work. The test values are large so I cannot debug. Please help. Thanks!
Is it Cheriton-Tarjan Algorithm?
https://books.google.co.uk/books?id=zxSmHAoMiRUC&pg=PA78&lpg=PA78&dq=cheriton-tarjan+algorithm&source=bl&ots=LQWYqzK7bq&sig=mmKjYZ7pevW3vkPD1Xmg7GC5BOI&hl=en&sa=X&ei=0AX4UsykO_Cp7AbWiICADg#v=onepage&q=cheriton-tarjan%20algorithm&f=false
Problem F can be solved with a set instead of a segment tree. Since we are finding a segment $$$(a_i,b_i)$$$ containing $$$x$$$ with the minimal value of $$$a_i$$$, we can remove all segments which are fully contained in some other segment. Thus, sorting remaining segments by $$$a_i$$$ is the same as sorting them by $$$b_i$$$, so we can keep them in a set keyed by $$$b_i$$$, removing segments if necessary.