Блог пользователя Tigutor

Проверка на простоту чисел тестом Миллера-Рабина: реализация и сравнение.(Miller-Rabin BPSW Test: realization)
Автор Tigutor, история, 8 лет назад, По-русски

Понадобилось мне сегодня проверить на простоту числа за время, куда меньшее корня квадратного из n, и сразу в голове всплыла статья с emaxx. Полез я туда, скопировал код, а он не работает. И не хотелось в нем разбираться, попытался найти в гугле — там тоже абсолютно ничего по сабжу нет. Вот и решил я написать свою реализацию.. Открыв wikipedia, можно увидеть замечательную запись:

Немного подумав(возведение в степень по модулю — log, предпосчет степеней двойки вообще за const), я порадовался вырисовывавшейся асимптотике и начал писать. Понимая, что на одну проверку уйдет 2log, но вероятность верного определения числа всего 3/4, мною было принято решение производить 5 проверок — в этом случае вероятность неверного решения будет всего 1/1024. Получился следующий код. Далее, была проведена проверка, я сдал задачу

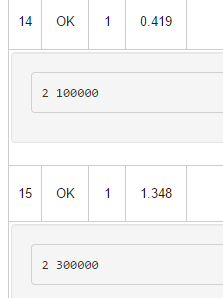
Как мы видим, худший тест выполнился за время чуть более одной секунды, тогда как решение за корень из n работает ровно одну секунду

Я уменьшил количество проверок до 3 и получил полностью рабочее решение с временем около 1с.

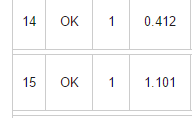
Поразительно то, что на таких маленьких входных данных тест Миллера-Рабина работает почти так же быстро, как и проверка за корень! Что уж говорить, что на больших числах проверка за корень не уложится и в 10 секунд, тогда как такой тест сработает за сотые доли секунды. Или, как вариант, найти все простые числа в диапазоне от 10^12 до 10^12 + 10^6

Решето Эратосфена умрет по дороге и из-за огромного количества памяти, и уж тем более по времени — ведь его асимптотика при нахождении всех простых чисел от N до K О(KloglogK), а асимптотика теста Миллера-Рабина — O((K — N)logK), ну и не забываем скрытую константу, равную 10. Внушительная разница, не правда ли?

На этом моё небольшое исследование подошло к концу, буду рад комментариям, оптимизации кода и другим проверкам этого алгоритма.
UPD Благодаря замечанию уважаемого AlexanderBolshakov была решена проблема с переполнением на огромных числах в степени по модулю и исправлено возведение в степень. К сожалению, это увеличило каждый log в асимтотике еще на log, но на огромных числах это не повлияло на время работы. Задача зашла без проблем.

  • Проголосовать: нравится
  • +9
  • Проголосовать: не нравится

»
8 лет назад, # |
  Проголосовать: нравится +10 Проголосовать: не нравится

Давай сразу выскажу замечания по теме:

  1. Если тебя хоть сколько-нибудь волнует производительность твоего кода, никогда не пиши бинарное возведение в степень рекурсивно. Каноничная итеративная реализация есть на е-максе, разберись в ней и вызубри ее так, чтобы мог закодить ее с закрытыми глазами на задержке дыхания.
  2. На том же е-максе описана очень полезная штука под названием "блочное решето". Как раз для случая [1012;1012 + 105]
  3. На идее блочного решета основан алгоритм, который годится для случая [10100;10100 + 105], а также практически используемый для генерации случайных больших простых чисел. Идея в том, чтобы заранее отсеять числа в заданном интервале, делящиеся на маленькие простые числа (к примеру, до 100), а уже потом запускать для оставшихся тест Миллера-Рабина.

При вычислении огромных чисел может произойти переполнение при вычислении по модулю(ибо модуль — огромный), как с этим бороться — пока не знаю, может быть у кого-нибудь появятся идеи?

Во-первых, можно свести умножение a * b к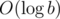 сложений ровно так же, как ab сводится к 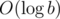умножений. Желательно написать функцию умножения поаккуратнее, избегая взятий по модулю. Во-вторых, можно воспользоваться длинной арифметикой. В-третьих, в 64-битном GCC есть нестандартный тип __int128.

→ Ответить
  • »
    »
    8 лет назад, # ^ |
      Проголосовать: нравится +3 Проголосовать: не нравится

    Спасибо за замечание, всё исправлено и работает на больших тестах.

    → Ответить
»
8 лет назад, # |
← Rev. 2   Проголосовать: нравится +1 Проголосовать: не нравится

Это довольно частый случай, когда "быстрые" алгоритмы на небольших значениях работают медленней, чем их наивная реализация. Недавно в "этой области" было сделано ещё одно открытие.

Кстати, существует одна модификация данного алгоритма, которую чуть быстрее написать/запомнить.
Но этот алгоритм может в две стороны ошибаться.

boolean isPrime(long num, int k) {
	if (num < 5) { return (num == 2) || (num == 3); }
	if (num % 2 == 0) { return false; }

	boolean prime = false;
	long sqrt = (num - 1) / 2;

	while (--k >= 0) {
		long a = (random.nextLong() & 0x7FFFFFFFFFFFFFFFL);
		a %= (num - 2);
		a += 2;
		long e = pow(a, sqrt, num);
		if (e == 1) { continue;	}
		if (e == num - 1) {
			prime = true;
			continue;
		}
		return false;
	}
	return prime;
}
→ Ответить