A. (link) In this problem you should do just that is written in the statement. At the first you should read all skills and multiply all levels of them by koefficient k. Next you should drop all skills which have level less than 100. After that you should add all new skills from the second list but only those thah are not present in the second list. At the end you should sort all skills by thier names and output them.
***
Problem with precision in this problem a bit shocked an author. This catch was not planned. Author's solution and all verifying solutions use integer arithmetic and think about probably problems didn't occur. In other side, it confirms following rule in the olympiad programming: be careful with comparation of floating numbers and if it is possible do it in integers.
B. (link) Solution of this problem is search maximum for all cases of sweets' distribution.
Common count of the distributions is Ck + n - 1n - 1, thah id always no mare than 6435. Let us define as current some distribution and calculate values zi = min(li + ci × 0.1, 1.0), where zi is probability that i-th senator vote "yes", li is loyality of senator and ci is number of candies that we should give i-th senator.
Now you can calculate propability of success in O(2nn). You should iterate ovel all masks of length n. 1-bits mean that corresponding senators vote "yes", 0-bits means that ones vote "no". Probability that this mask happen is mmask = П(zi × [i - thsenatorvote"yes"] + (1 - zi) × [i - thsenatorvote"no"]), where [true] = 1 and [false] = 0. Now for every mask you should find propability that player's proposal will be approved. It is smask = 1 if number of votes "yes" more than half of n and smask = A / (A + B) it other case, where B is the sum of levels of senators that voted "no". So, propability for current distribution is 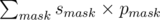 .
.
Solution has complexity O(Ck + n - 1n - 12nn).
***
This problem was plannes more harder (like D problem). But later we decided make it more easier))
C. (link) There you can see that if at least one item has empty slots then you can redistribute the residents in any order. This assertion can be easily proved. In other case you cannot move residents.
Yet another thing that you can see here. In the optimal equipment all items have maximal possible paremeters. Moreover this items with thier residents do not affect each other. So, you can split all items and all residents by thier classes and types and three times solve same problem for groups (weapon, gladiators), (armor, senrties), (orbs, physicians).
So, there are 2 cases: you cannot move residents and you can move ones.
1. For every item you should find its paremeter considering residents that are living inside it. After thah you should choose item that have maximal parameter.
2. Here you should sort all residents by desreasing its bonuses. Next you should iterate over all items, try put maximal count of strongest residents and calculate resulting value of parameter. Now you shouls choose item that have maxumal parameter.
In the second case some catch exists. In the three choosen items you can have more empty slots than you had at the beginning of moving. It is impossible because you cannot drop residents. Therefore you should, for example, put as most as posiible unused residents into empty slots of three choosen items.
***
Initially we planned the first case as catch and put it into pretests, but not into samples. But because contest turned very hard, we put it into samples.
D. (link) This problem can be solved by data structure like disjoint set union (dsu) with compression paths heuristic.
Every vertex of dsu is geo-panel and every connected component is the set of one-colored geo-panels. All important information stores in the leader of component. It is size of group (count of geo-panels in it), its color and list of geo-symbols in this group that not destroyed.
You should create queue that described in the statement. There you should store geo-symbols. Every symbol is color and position of map where this symbol was placed.
Also yoy should create associative array (like std::map in с++), that returns leader of group in dsu by color of this group.
At last you should create array with size 2n × 2m and store in it path of infinite spiral. This array you can use for easily sorting geo-symbols before putting its into queue.
This system of data structures allows fast emulate all process.
So, let put the first geo-symbol into queue, generate spiral array and set dsu and associative array into initial state.
Now you can do following operations while queue is not empty:
You should remove geo-symbol from front of queue. Let call it current geo-symbol. By its coordinates using dsu you can find group in which current geo-symbol is placed. Next you should compare colors of group and geo-symbol and understand this group should be repainted or not.
If group should be repainted you should add size of its group to global answer. After that you should sort all geo-symbols in this group using spiral array. In this order you should insert these geo-symbols into back of queue and clear list of qeo-symbols in the group. Now you should repaint group and replace associative array.
You can see that some situation can happen. Now you can have two groups with equal colors (you can fast know it using associative array). These groups chould by united. You should set parent of group that you this moment repainted the second group and increase size of the second group by size of first group.
You can prove that this algorithm works in O(nmlognm).
E. (link) At the beginning you should estimate maximal answer what you can get. It equals 42. This answer you can get from following obvious maximal test:
8 10 10
9 10 10
10 10 10
Common number of states in which character can be without regard to position is 8. 2 for moved/not-moved multiply to 4 for nobody-lifted/lifted-A/lifted-B/already-threw.
Total number of states is (8 * 42)3 = 37933056. This count of states can be easily stored in memory.
Solution is DFS or BFS from initial state. Maximal position in reached states is answer..
Why it fits into time limits? In fact you can do about 60 moves from every state.
Point is that most of states will be not reached. For example, following heuristics confirm it:
1. If one character is lifted by another one, thier positions are equal.
2. States where one characher lifted by both anothers are incorrect.
3. In positions with big numbers no more than 2 characters can be. In positions with very big numbers no more than 1 character can be.
Also from more states possible little number of moves. They are states in which some characrers already moved or already threw somebody.
You can find exact number of moves only after writing solution. Run on the maxtest shows that number of moves about 2 × 108. So, this solution fits into time limits. You should just accuracy write it.
***
Author's solution on С++ works about 0,3sec. Also we have solutions on Java, whish works 2,8sec and 0,8sec. In the first solution for every move new object is created. It calls some number of garbage collection. In the second solution this problem is fixed. But in order to solutions on Java like the first one pass tests, TL was increased to 3sec.
I'm sorry for delay with thanslation into English.











Let's call it EPS=1e-9
Just think of it like that(pls correct me if i'm wrong):
any number within EPS of a float/double number N is considered to be equal to the number(that is if number X is between N-EPS and N+EPS, then X considered equal to N)
1. For A==B use: abs(A-B)<EPS or equivalently: B-EPS<A<B+EPS
2. For A<B use: A<B-EPS
3. For A<=B use: A<B+EPS
Now for problem A, you need to check:
K*level < 100
==> K*level < 100-EPS
==> K*level +EPS < 100, so you can calculate (int) (K*level+EPS) then compare with 100 or also compare directly K*level< 100.0-EPS
so we need to check K*level<100 NOT K*level<=100
NO, you need to take care of precision in ALL cases: <,<=,==.
For A<B you need to do A<B-EPS because we are considering any number between B-EPS and B+EPS to be equal to B. it's similar for A<=B.