1. Lucky Number (Div2 A)
In this problem you just need to find a number of lucky digits in n and output YES if it number is equal to 4 or 7, NO otherwise.
2. Lucky String (Div2 B)
To solve this problem you need to notice that result is a prefix of string abcdabcdabcd...abcd and output first n characters of this string.
3. Lucky Sum of Digits (Div1 A, Div2 C)
Let result number contains a digits 4 and b digits 7. Obviously, that a * 4 + b * 7 = n. Loop through all values of b. If we know b, we can calculate a, 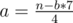 . Among all pairs (a;b) we need to choose one with a + b minimum. Among all that pairs we need to choose one with b minimum. Output will be an integer 444...444777...777, here number of digits 4 equal to a, number of digits 7 equal to b.
. Among all pairs (a;b) we need to choose one with a + b minimum. Among all that pairs we need to choose one with b minimum. Output will be an integer 444...444777...777, here number of digits 4 equal to a, number of digits 7 equal to b.
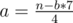 . Among all pairs (a;b) we need to choose one with a + b minimum. Among all that pairs we need to choose one with b minimum. Output will be an integer 444...444777...777, here number of digits 4 equal to a, number of digits 7 equal to b.
. Among all pairs (a;b) we need to choose one with a + b minimum. Among all that pairs we need to choose one with b minimum. Output will be an integer 444...444777...777, here number of digits 4 equal to a, number of digits 7 equal to b.4. Lucky Probability (Div1 B, Div2 D)
Let L[i] - i-th lucky number, starting from 1 (L[0] = 0, L[1] = 4, L[2] = 7...). At first choose first k lucky number, then second k numbers and so on. For each of that group lets find answer, result will be a sum of each of this probabilities. Let index of current first number if i, last - j (j = i + k - 1). Then we need to find intersection of intervals [pl;pr] and (L[i - 1];L[i]], and also [vl;vr] and [L[j];L[j + 1]), product of that values will be a number of ways in which p < v, similarly for p > v. Sum of all that values for each group will be a total number of ways, then result = total number of ways / ((pr - pl + 1) * (vr - vl + 1)).
5. Lucky Tree (Div1 C, Div2 E)
Solve this problem using dynamic programming. Consider that root of a tree is vertex with number 1. Let F(x) - number of vertex in subtree of vertex x for which there is a path containing lucky edge. We will calculate F(x) using recursion. If x is a leaf, than F(x) = 0. Else, if there is an edge from x that leads to y and this edge is lucky, then to F(x) we need to add C(y), otherwise we add F(y), here C(y) - number of vertex in subtree of y, including y. But, to solve this problem we need to know also F'(x) - number of vertex which are not in subtree of x and there exits a path from x to that vertex that contains lucky edge. For a root of tree, F'(x) equals to 0. We should go recursive from root, and if we are in vertex x now, we suppose that F'(x) is already calculated. If from x we can directly go to y and that edge is lucky, then F'(y) = C(0) - C(y), otherwise F'(y) = F'(x) + F(x) - F(y).
After that, result equals to 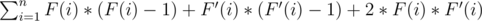 .
.
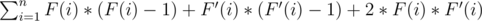 .
.6. Lucky Sorting (Div1 D)
At first, if our array is already sorted, just return 0. Otherwise, if there is no lucky number in A, then output - 1. Otherwise, let B is sorted A (array from input). Now, for all numbers in A we know a final position in B. Let k is an index of minimal lucky number in A. If we want to place integer from position i to j, we need A[j] to be lucky number. If is not so, we just Swap(A[j], A[k]), then A[j] contains lucky number. After that we can Swap(A[i], A[j]) and number A[i] is on position j. So, to place one number to it's position in B, we need at most two operations and total number that replacements will be not more than n, so answer'll contain at most 2n operations.
7. Lucky Interval (Div1 E)
That is only onw variation of solution, there are diffrent other, which uses same thinking.
With constraints for a and b to 107 problem can be solved using KMP algorithm: consider a string F(1)F(2)F(3)F(4)...F(3 * 107). We need to find first occurrence after index a of string F(a)F(a + 1)F(a + 2)...F(a + l - 1). Complexity of that algorithm is O(a + l), obviously, that fails on time and memory. Lets try to optimize this algorithm using some facts from "Lucky numbers theory".
Split all number interval on block with sizes 100: [0;99], [100;199] and so on. Introduce a concept "class of block". Class number of a block equals to F(i / 100), where i - any number from that block. There are 8 different block classes. There are at most 6 consecutive blocks with same class. All that can be seen using brute force.
Note #1: if l ≥ 1000, then 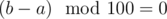 .
.
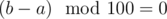 .
.Proof: consider a string F(100 * k)F(100 * k + 1)...F(100 * k + 99). Number of different that strings is equal to number of different classes. For example, for first class that string looks like this:
00001001000000100100000010010000001001001111211211000010010000001001001111211211
00001001000000100100
for second:
11112112111111211211111121121111112112112222322322111121121111112112112222322322
11112112111111211211
and so on. According to the structure of that strings, different block (by classes) can't intersect (there'll be no match). Hence, any sequence of of consecutive blocks which contain at least two blocks of different classes will match only with the same sequence, so shift will be multiple of 100. Since there is no more than 6 consecutive blocks with the same classes, if l ≥ 1000 then, obviously, this interval will contain at least two blocks with different classes.
So, problem with l ≥ 1000 can be solved using KMP with complexity O((a + l) / C), where C equals 100, let function that do that is named Solve(l, r).
Now we need to solve problem for l < 1000. At first, let a' is minimal number that F(a') = F(a), F(a' + 1) = F(a + 1), ..., F(a' + l - 1) = F(a + l - 1), a' / 100 = a / 100, that can be done using brute force. Then result is the minimum of next numbers:
- r = Solve(a', a' + l - 1);
- Minimum r', for which r - r' < = 1000, r' > a, F(r') = F(a), F(r' + 1) = F(a + 1), ..., F(r' + l - 1) = F(a + l - 1).
- Minimum a'' for which a'' > a, a'' - a ≤ 1000 and F(a'') = F(a), F(a'' + 1) = F(a + 1), ..., F(a'' + l - 1) = F(a + l - 1).
That solves the problem of some non-100-multiple shifts, but that may be a doubt. Consider input interval is in just one block with class C. Then, probably, it is better to go to block with class C + 1, for example (397;1) → (400;1). Actually, second point solves that problem, because if block with class C + 1 is before C (and only in that case we will choose C + 1), then next block after current have class C + 1. To proof this we can use this note (which can be proofed using brute forces):
Note #2: if there is two consecutive block, then absolute difference between they classes is not more then 1.
Hence, if after block C (in which input interval is) goes block with class C - 1, then we will go to block C before C + 1, otherwise we will choose it (C or C + 1).
Thus, problems solves by accurate analysis all moments. Complexity of solution is O((A + L) / 100), my solution works 1.5 sec. and use 250 mega bytes of memory.
There are also solution which decompose of blocks with sizes depentding on l, that one work faster.











For problem lucky tree. ..
I have found another algorithm within some participator's code ...
(... which is much easier to implement than above .. )
For each "lucky edge", maintains a group of component by Union-Find-Set.. .Igore each "lucky edge", maintains the residual graph by dsu。
Then you can get the result by some combinatorics method ..
Could anyone explain this thought further ? ..
Let's erase all lucky-weighted edges from the tree. Then, any two vertices are in different connected components if and only if the path between them in the original tree contained a lucky edge.
So it's sufficient to ignore lucky-weighted edges while reading the input, compute the connected components' sizes (using BFS, DFS or Union-Find), and then, for every vertex v, let's denote by f(v) the number of vertices in different connected components than v (unreachable from v). Let's count the triples beginning with v. Their number is f(v) * (f(v) - 1). We do this for all v (or alternatively for whole connected components at once) and return the sum.
Hope that this clarifies the approach. I think this solution is not only easier, but it also works for arbitrary connected graphs, not just trees (if we replace "the way" by "any way" in the problem statement).
。paulocezar && dj3500。。Thanks a lot 。!!。:)
Thanks Before :D
P.S : I'm using Java
The problem is you shouldn't build string then print it. it takse much time. particularly in java.
you must directly print characters.
something like this: for(int i=0 ; i<n ; i++) System.out.print((char)(i%4+'a'));
if i just thought twice before submitting I'd be in div.1 now.
The key is to notice that there not so many lucky numbers: 2046 in the range [1,10^9]
Now if there are k lucky integers between min(v,p) and max(v,p), they must be
consecutive: There is some i such that it's the set L[i] .. L[i+k-1].
Iterate over i, add the probability that min(v,p)<=L[i] and L[i+k-1] <= max(v,p).
There is a catch with k=1: the case where min(v,p) == L[i] == max(v,p) is
counted twice that way, so it has to be corrected.
For Lucky sum of Digits, is the second part of the statement necessary? As in, if we have two pairs (a1,b1) and (a2,b2) such that a1+b1 = a2+b2, then it has to be that a1 = a2 and b1 = b2. We don't need to check again amongst those pairs.
I solved Div1 A using an observation that there can't be more than 6 4s together. If there are, those 7 or more 4s can be replaced by 4 7s as 7 * 4 = 4 * 7, which obviously shall be a smaller number. Secondly, all 4s should be at the beginning so as to make the number as small as possible, Thus I counted the number of 7s till the number is less than or equal to 24 and divisible by 4. Incase it is never divisible by 4, I output -1. Else, I just add 4s and that's it. Code: https://codeforces.com/contest/109/submission/52615818
Thanks. good editorial