CodeChef invites you to participate in the March Cook-off 2015 at http://www.codechef.com/COOK56.
Time: 22nd March 2015 (2130 hrs) to 23rd March 2015 (0000 hrs). (Indian Standard Time — +5:30 GMT) — Check your timezone.
Details: http://www.codechef.com/COOK56/
Registration: Just need to have a CodeChef user id to participate.
New users please register here
- Problem Setter : Vitaliy Herasymiv
- Editorialist: Amit Pandey
- Problem Tester: Istvan Nagy
- Contest Admin: Praveen Dhinwa
- Russian Translator : Sergey Kulik
- Mandarin Translator: Gedi Zheng
It promises to deliver on an interesting set of algorithmic problems with something for all.
The contest is open for all and those, who are interested, are requested to have a CodeChef userid, in order to participate.









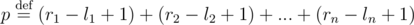 .
.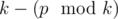 .
.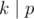 , or just output
, or just output 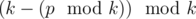 .
.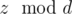 doesn't change. Indeed,
doesn't change. Indeed, 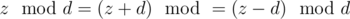 . This means that there is not answer if there are two different points for which
. This means that there is not answer if there are two different points for which 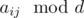 is diffrent.
is diffrent.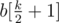 (median element). Why to median? Suppose that we make all numbers equal to non-median element with index
(median element). Why to median? Suppose that we make all numbers equal to non-median element with index 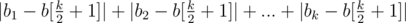 , divided by
, divided by  it is 0). It turns out that for each
it is 0). It turns out that for each 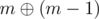 no bit disappear, at
no bit disappear, at  no bit disappear, ..., at
no bit disappear, ..., at 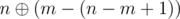 no bit disappear. So, it is good to assign exactly that integers to our permutation, i. e.
no bit disappear. So, it is good to assign exactly that integers to our permutation, i. e. 
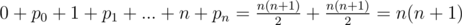 .
.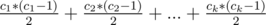 . This gives us
. This gives us 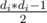 multiplied by the number of vertices in subtree, where
multiplied by the number of vertices in subtree, where 

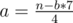 . Among all pairs
. Among all pairs 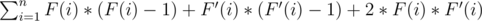 .
.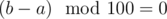 .
.
