161A - Dress'em in Vests!
Consider troopers in the sorted order, as in the input data. One can prove that for the current (minimal) trooper the best choice is the vest with the minimal possible bj.
So we can solve this problem using “moving pointers” method. The first pointer iterates over troopers and the second one chooses minimal unused vest that bj - x ≥ ai.
The complexity of the solution is O(n + m).
Idea: Burunduk1
161B - Discounts
This problem can be solved greedy. Let us have x stools. One can prove that it is always correct to arrange min(k - 1, x) maximal stools into min(k - 1, x) carts one by one. All remaining stools and pencils should be put into remaining empty carts. Finally, we have either zero or one empty cart.
161C - Abracadabra
Consider the case when the maximal character in the string is in the answer. Then the answer equals min(r1, r2) - max(l1, l2). Otherwise, we cut both strings around this character (here we might get empty strings) and run the algorithm recursively for every pair of strings we get. One can prove that this solutions works in O(k), where k is the values of the maximal character.
Idea: avm
161D - Distance in Tree
This problem can be solved using dynamic programming. Let us hang the tree making it rooted. For every vertex v of the tree, let us calculate values d[v][lev] (0 ≤ lev ≤ k) — the number of vertices in the subtree, having distance lev to them. Note, that d[v][0] = 0.
Then we calculate the answer. It equals the sum for every vertex v of two values:
- The number of ways of length k, starting in the subtree of v and finishing in v. Obviously, it equals d[v][k].
- The number of ways of length k, starting in the subtree of v and finishing in the subtree of v. This equals the sum for every son u of v the value:
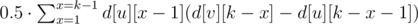 .
.
Accumulate the sum for all vertices and get the solution in O(n·k).
Idea: Burunduk1
161E - Polycarpus the Safecracker
We need to count the number of symmetric matrices with a given first row, where each row is a prime number.
Since the matrix is symmetric, it is determined by its cells above or on the main diagonal. Let's examine all possible values of digits above the main diagonal (at most 106 cases). Now the values of the remaining unknown digits (on the main diagonal) are independent of each other because of each of them affects exactly one row of the matrix. Therefore, it is enough to count independently the number of possible values for each of the digits on the diagonal, multiply them and add received number to answer.
Moreover, it's possible to pre-calculate such numbers for each position of unknown digit and for each collection of known digits.
These observations are enough to pass all the tests.
One could go further, examining each next digit above the main diagonal only if it's row and column can be extended to prime numbers by some digits, unknown at moment of this digit placing. Such a solution allows to find answers for all possible tests in the allowed time, but it wasn't required.
Idea: avm
All the stuff around the problems has been prepared by (in alphabetic order): arseny30, at1, avm, Burunduk1, Burunduk2, burunduk3, Gerald, levlam, MikeMirzayanov











Nice :) Problem D could also be solved much faster using Splay Tree... if you sort the solutions by execution time, you can see all the fastest ones used this. Oh and hey, they all used actually the exact same code:
1343350 by XusuoFestival rank 235
1342455 by suhang1994 rank 147
1343283 by whitesky rank 403
1343446 by mjmjmj rank 207
And so on... what a coincidence that they all have the same code.
1349546 is even faster asymptotically, it's just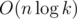 . That's because it uses hash tables instead of splay trees.
. That's because it uses hash tables instead of splay trees.
How is it using hash tables? The solution looks like it is just the N*K dp solution using an iterative dfs by a manual stack. Can you explain further how the solution works algorithmically? I don't use python much.
O(nk) solution won't pass in Python because of it's high overhead.
Here's the same algorithm in Java:
Sorry I really can't see at all why this solution would be O(n log k). Isn't
for (Entry<Integer, Integer> e: result2.entrySet())going to go through all k values in the map? And you are doing this for all children of all nodes. If that is so, it will be O(nk).Read the large comment very carefully.
It says that there are two types of merges: when both subtrees of size at least k and when one of the subtrees has size less than k.
The first type merges can only be done n / k times. So it gives O(n), for all merges, since one merge is done in O(k).
In the second type of merge, since you iterate over map of small subtree and add them one by one, every vertex will be iterated over O(log(k)) times, because every time it is being iterated over, the size of its subtree gets twice larger. Since it is in subtree of size at most k, this vertex is touched O(log(k)) times, while it takes part in second type of merges. So this gives O(n log(k)).
Thanks to all who replied. I think I get it, but it isn't got to do with the hashing at all right? In fact I can do this same optimization with the O(nk) DP by remembering the maximum length reached for the node so far, iterating over the smaller of the current array and that of the next child and propagating a pointer to the current maximum length array...
It is. You can add to Hash Table in O(1) time, so k additions give O(k).
Everything you do is iterating over Hash Table, adding and search for elements in it. Iterating is O(1) time per element, addition and searching is O(1).
The solution is O(n log(k)) operations with Hash Table, since all of them are done in O(1) time, you get overall solution complexity O(n log(k))
I didn't get your point at first.
It seems that you are right.
Look carefully at this:
I always iterate over the smaller of the two maps. Every time I go through a value, I move it to a map which becomes at least twice larger. That's why I go through each value at most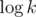 times.
times.
There is also a solution using divide and conquer that runs in N log N for arbitrary K. My solution (1346501) implements this idea except I was lazy and did the N log^2 N version. Change the graph splitting step to be O(N) instead of N log N and my solution becomes N log N. The N*K is easiest to code for this bound though. =) I like this problem because of the variety of approaches that can be used.
Here is the N log N version: 1354146
N*log(N) with a simple idea (1353450, from "vvi graph");
It's actually very obvious that they are copies, because if you look at the start of int main, they all have this: ~~~~~ e[++l]=y,next[l]=lis[x],lis[x]=l;cost[l]=1; e[++l]=x;next[l]=lis[y],lis[y]=l;cost[l]=1; ~~~~~ Notice the commas and the semicolons. They both made the same formatting inconsistency.
Could you explain how to prove the O(k) bound for running time in C?
For convenience we define a substring as a interval on a segment [1,2^p-1], where p marks the depth of recursion.
The main point of the standard algorithm is to divide a request on [1,2^p-1] into at most 2 requests on [1,2^(p-1)-1].(2 is correct, because when there are 4 subrequests two of them can be regareded trivial. See next paragraph.)
It's obvious that if one of the interval in request is full or empty,this request can be solved in O(1) without recursion.We call these requests trivial.(Futhermore, when a interval is totally covered by the other,this request can be regarded trivial. So requests of two prefixes or suffixes are trivial, because the condition of covering is hold.)
Similar to a segment tree, we can prove that on each level of recursion, there will be at most 2 non-trivial interval of substring A,2 non-trivial interval of substring B,so the maximal non-trivial requests on each level is 4.
thus,the time complexity for the recursive algorithm is proved O(k).
I don't think it's that simple or perhaps I misunderstood something. You say that a single request on level p results in 4 requests on level p-1. This gives you exponential time complexity, not linear.
It's correct that single request on level P can result in 4 requests on level p-1, but this means all 4 requests on level p-1 are non-trivial. That is, No more non-trivial requests on level p-1. Linear time complexity still hold.
If you dont understand, think why a interval on a segment tree can be divided into two intervals on next level, but its time complexity is O(h),not O(2^h), where h is the height of segment tree.(at most two non-trivial intervals on each level.)
(Sorry for my poor expression...As a Chinese,I'm not a native speaker of English.)
I disagree that all 4 requests are trivial. I'll give an example with k=3. Lets say we have the following request L1=3, R1=6, L2=5, R2=12. We divide it into two requests on level k-1: L1=3, R1=6, L2=5, R2=7 and L1=3, R1=6, L2=1, R2=4. These two requests are not trivial. You would have to go at least one step further to prove that you are left with just trivial requests in some small, constant number of steps.
What's written before is "this means all 4 requests on level p-1 are non-trivial." I think your example makes no sense this time.
I want to ask that can Problem D is solvable by applying DFS of k length on each and every vertices??? Please reply admin...
If you try that on the following graph:
you would perform O(n^2) operations when k >= 2.
I have written a tutorial about VK practice session but I can't attach it to the corresponding site. What can I do?
In problem D's tutorial(above), for each v, d[v][0]=0;
Now for first test case,
for vertex 2, first value is 1. for second value- 0.5(d[3][0]*(d[2][1]-d[3][0])) + 0.5(d[5][0]*(d[2][1]-d[5][0])) = 0(as d[3][0]=0 and d[5][0]=0), but shouldn't it be 1(for path 3->5). Please tell me where am i going wrong.
Thanks..
d[v][0]=1 ( Base Case ).
Because the vertex v is itself a part of its subtree.
Taking d[v][0]=0 gives wrong answer.
Can someone explain the recurrence relation for problem D?
How did they get d[u][x-1](d[v][k-x] — d[u][k-x-1])?
We are iterating over the subtree where one end of the path is (u). The path consists of two segments: - one inside of u's subtree (length is x, which we apart iterate over), there are d[u][x-1] of them - another one outside of u's subtree (but still within v's subtree), the length of this segments is k-x (counting from v); there are d[v][k-x]-d[u][k-x-1] of them
Give or take ±1 everywhere:) it's been 8 years after all.
Why did they subtract d[u][x-1] — d[u][k-x-1]?
Sorry, I'm new to dp so I don't know how to get the recurrence relation.
It's a bit different as compared to what you wrote.
The overall amount of vertices in v's subtree on depth (k-x) is d[v][k-x]. We should not count the vertices that are in u's subtree though, because in this case we are looking only at the paths that would go through v. So we have to subtract that amount, which is d[u][k-x-1]. The (-1) here is because u is exactly one level below v.
This might help : https://codeforces.com/blog/entry/76080?#comment-604916
I have tried to write a beginner friendly solution for D :)
Did someone solve D using LCA in O(1) per query? My attempt: 140424972
O(1) per query still makes it O(n^2) which obviously won't pass.