161A - Dress'em in Vests!
Consider troopers in the sorted order, as in the input data. One can prove that for the current (minimal) trooper the best choice is the vest with the minimal possible bj.
So we can solve this problem using “moving pointers” method. The first pointer iterates over troopers and the second one chooses minimal unused vest that bj - x ≥ ai.
The complexity of the solution is O(n + m).
Idea: Burunduk1
161B - Discounts
This problem can be solved greedy. Let us have x stools. One can prove that it is always correct to arrange min(k - 1, x) maximal stools into min(k - 1, x) carts one by one. All remaining stools and pencils should be put into remaining empty carts. Finally, we have either zero or one empty cart.
161C - Abracadabra
Consider the case when the maximal character in the string is in the answer. Then the answer equals min(r1, r2) - max(l1, l2). Otherwise, we cut both strings around this character (here we might get empty strings) and run the algorithm recursively for every pair of strings we get. One can prove that this solutions works in O(k), where k is the values of the maximal character.
Idea: avm
161D - Distance in Tree
This problem can be solved using dynamic programming. Let us hang the tree making it rooted. For every vertex v of the tree, let us calculate values d[v][lev] (0 ≤ lev ≤ k) — the number of vertices in the subtree, having distance lev to them. Note, that d[v][0] = 0.
Then we calculate the answer. It equals the sum for every vertex v of two values:
- The number of ways of length k, starting in the subtree of v and finishing in v. Obviously, it equals d[v][k].
- The number of ways of length k, starting in the subtree of v and finishing in the subtree of v. This equals the sum for every son u of v the value:
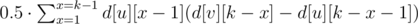 .
.
Accumulate the sum for all vertices and get the solution in O(n·k).
Idea: Burunduk1
161E - Polycarpus the Safecracker
We need to count the number of symmetric matrices with a given first row, where each row is a prime number.
Since the matrix is symmetric, it is determined by its cells above or on the main diagonal. Let's examine all possible values of digits above the main diagonal (at most 106 cases). Now the values of the remaining unknown digits (on the main diagonal) are independent of each other because of each of them affects exactly one row of the matrix. Therefore, it is enough to count independently the number of possible values for each of the digits on the diagonal, multiply them and add received number to answer.
Moreover, it's possible to pre-calculate such numbers for each position of unknown digit and for each collection of known digits.
These observations are enough to pass all the tests.
One could go further, examining each next digit above the main diagonal only if it's row and column can be extended to prime numbers by some digits, unknown at moment of this digit placing. Such a solution allows to find answers for all possible tests in the allowed time, but it wasn't required.
Idea: avm
All the stuff around the problems has been prepared by (in alphabetic order): arseny30, at1, avm, Burunduk1, Burunduk2, burunduk3, Gerald, levlam, MikeMirzayanov










