UPD1:
Editorial to Problem <>
First of all note that merchants will pay only for those edge which are bridges. All other edges don’t match as after their deletion graph stay connected and between any nodes of graph the way stay. So first step to solve problem is to search bridges. Use this algorithm which works at O(n + m)
After deletion all the graph bridges graph is divided for some components of connectivity (maybe one component). Let’s build new graph in which recieved components will be nodes and bridges — edges. This graph will be a tree. The graph is connected therefore the tree is connected. The edges correspond to bridges therefore there is no cycles in the tree.
Note that the number of denarii means the pay of every merchant — is a distance between some the nodes in a new graph. But as this graph is a tree this distances can be easily find out using LCA search algorithms for two nodes. In this problem one should use the simplest LCA search algorithm which accomplish the preprocess for 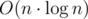 and handle one request for
and handle one request for  . The complexity of computations id
. The complexity of computations id 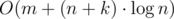 .
.
One can solve this problem easier. Let’s build a graph recursive pass-by initial graph and weight its edges. The edges with weight equals 1 will have bridges and others will have weight equals 0. So after all these reductions for solving problem it will be enough to compute the distance between two nodes in the graph recursive pass-by initial graph.
UPD:
Editorial to Problem <<Beaver's Problem — 2>>
Solving this problem can be divided into two parts:
- Noise deletion on the picture;
- Fugures' classification.
For noise deletion one can use the following methods:
a. Do following steps: scan picture and build new on using it. If sone black pixel have white neighbours, we make it white. During thise steps we get rid of almost all noise on the picture. Then we make inverse opreation replacing all white pixels with black. So we get rid of almost all noise inside the picture.
Note, that after all these opreations noise can stay as little black components. And some figures can lose their connectivity. These problems can be solved by deletion little black components and then unite near black components.
b. But one can use easier way. Highlight black components and then cast away little ones. If to look closely to the texts in real under even distribution of the noise there is no little black components and it is not losing connectivity. However previous way is more reliable.
The simplest way to classificate figures is to compare distributions of the distances from all the figure pixels to centre of the every figure. The centre can be calculated as average of the all points coordinates of the figure. Ditributions can be compared by expectation values and variations.
An Editorial to Problem <>
Let’s iterate through the cells of the hash table with step m (modulo h). So, all cells are separated into some cycles modulo h (all cycles have the same number of elements). It can be proven that the number of cycles is gcd(h, m) and the number of elements in each cycle is h / gcd(h, m). How can we use this property? The element with fixed hash-value will be added into some (next) cell in the corresponding to element’s hash-value cycle.
So, we can process each cycle separately. To do this effectively (we want to solve large test package) we have to use any tree-structure like segment tree or combination of Fenwick tree with binary search.
An effectiveness of solution with segment tree is 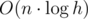 , of solution with Fenwick tree —
, of solution with Fenwick tree — 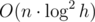 .
.
An Editorial to Problem <>
Let’s consider two different ways to solve this problem. Note that firstly (before finding correct magic square) we can easily determine the value of s. This value equal to the sum of all given numbers divided by n. So next, we will use this value.
The first way to solve problem is brute force. This way based on two main ideas:
- We can determine some square elements during the brute force using already fixed values. For example, if we have fixed three of values on the main diagonal, we can easily determine the fourth value. This trick decrease the number of brute force iterations.
- We can rotate (or mirror) magic square without breaking his magic properties.
The second way use discrete-optimization approach. Let’s consider the function Q = |sum1 - s| + ... + |sumt - s|, where |x| — the absolute value of x, t = 2 * n + 2, sum1, .., sumn — the sum of elements in one row, sumn + 1, sum2n — the sum of element in one column, sumt - 1 — the sum of elements on the main diagonal, sumt --- the sum of elements on the secondary diagonal.
So, we want to find such permutation of the given elements that make our function as small as possible (We want to obtain zero). One way to do this: pick the random permutation. Try to make swaps in this permutation using greedy strategy (try to make swaps that make our function better). Let’s do 1000 swaps. If we obtain Q = 0 — we have found answer, else Q > 0 -- pick another random permutation and repeat this process again.
An Editorial to Problem <>
It is the simplest task of the set. The solution is based on greedy algorithmm.
First of all, we need to zero out a1. One needs to make a1 steps with i = 1 and some t on each step. Which t is the most efficient? The maximum t, where 1 + 2t ≤ n. In that case later zeroing out longer prefixes of the sequence will take less steps. Having zeroed a1, we will write a current answer and notice that we reduce the task to the smaller one — sequence becomes one element shorter.
The complexity of a solution 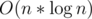 or O(n) — depends on implementation.
or O(n) — depends on implementation.
One can solve the task in a different way. To start from, the task can be solved for each element ai separately. In other words, if we fix some k, contribution of each ai to an answer can be counted separately.
We fix some ai. Then we find maximum j so that i + 2j ≤ n. Evidently, that for every k < i + 2j, contribution of ai to the answer equals ai. In other words, one needs to make ai steps with transition to ai. Further we need to find maximum u, so that 2j + 2u ≤ n. Notice that u < j. Contribution of ai to the answer is equal 2 * ai, for every k that i + 2j ≤ k < i + 2j + 2u. Then we find q that i + 2j + 2u + 2q ≤ n, and so on ...
A corresponding sequence of powers of 2 should be found for each element ai. Evidently, that overall complexity of this process is 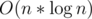 .
.
Now we need to calculate an answer. It can be done, for example, like that: we will store the array bi — the change of the answer at the transition from i to 4i + 1. This array is formed in a trivial way during construction of sequences of powers of twos. Then it is easy to get the answer.
The overall complexity of the solution equals 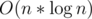 .
.
An Editorial to Problem <>
Here one can see author's solution.











Aaah, the local optimization of the functional trick in D — just like a boss! Magic squares — magic solution!
How to solve problem B2 Military Trainings?