How to calculate (a! / b!) % mod where n is 1<=n<=20000000, m is 1<=m<=n and mod is a positive integer ?
→ Pay attention
→ Top rated
| # | User | Rating |
|---|---|---|
| 1 | ecnerwala | 3649 |
| 2 | Benq | 3581 |
| 3 | orzdevinwang | 3570 |
| 4 | Geothermal | 3569 |
| 4 | cnnfls_csy | 3569 |
| 6 | tourist | 3565 |
| 7 | maroonrk | 3531 |
| 8 | Radewoosh | 3521 |
| 9 | Um_nik | 3482 |
| 10 | jiangly | 3468 |
→ Top contributors
| # | User | Contrib. |
|---|---|---|
| 1 | maomao90 | 174 |
| 2 | awoo | 164 |
| 3 | adamant | 161 |
| 4 | TheScrasse | 159 |
| 5 | nor | 158 |
| 6 | maroonrk | 156 |
| 7 | -is-this-fft- | 152 |
| 8 | SecondThread | 147 |
| 9 | orz | 146 |
| 10 | pajenegod | 145 |
→ Find user
→ Recent actions
↑
↓
Codeforces (c) Copyright 2010-2024 Mike Mirzayanov
The only programming contests Web 2.0 platform
Server time: Apr/26/2024 23:16:36 (k3).
Desktop version, switch to mobile version.
Supported by
User lists


| Name |
|---|











If you want to avoid multiplicative inverses, as the limits are <= 2e7, you can create a segment tree. If you divide a! by b!, you want to multiply the numbers b+1, b+2,....a. You can use a segment tree to do each query in O(logn), after building the segtree in O(n). You can also use a sparse table (similar to that explained in this [Topcoder tutorial](https://www.topcoder.com/community/data-science/data-science-tutorials/range-minimum-query-and-lowest-common-ancestor/#Sparse_Table_(ST)_algorithm)) to speed it up and solve each query in O(1), after preprocessing in O(n*logn). Note that this approach will work due to low limits (2e7).
UPD: The sparse table approach will also be O(logn) and not O(1). See FatalEagle's comment. :)
How to build segtree in O(n) time?
UPD. Yes, O(4*N) = O(N). My mistake.
Segment tree is usually built in O(N) — it is a simple dfs.
Can you describe the sparse table approach in more detail? The one in the tutorial seems to rely on the fact that counting the same element twice in the min function won't change the result.
Aah, right. My bad. The sparse table approach will also be logn, and not constant time, due to the reason you pointed out above. :)
There is a way of building sparse table in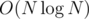 so that you won't have to consider element twice.
so that you won't have to consider element twice.
I'm not completely sure that this is called sparse table, but as far as Burunduk1 told me, it has something to do with it.
You have to do something like Divide & Conquer optimization.
Consider that you now need to precalc something for the interval [L;R] You should take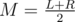 and calculate answers for queries [M;M], [M;M + 1], ..., [M;R] Calculate same thing for queries [M - 1;M - 1], [M - 2;M - 1], ..., [L;M - 1]
and calculate answers for queries [M;M], [M;M + 1], ..., [M;R] Calculate same thing for queries [M - 1;M - 1], [M - 2;M - 1], ..., [L;M - 1]
Now you can answer any query [X;Y], such that X ≤ M ≤ Y if you can merge answers for [X;M - 1] and [M;Y] in O(1)
Now we can deal with any query that consists M and we have to deal with intervals [L;M - 1] and [M + 1;R].
We have wasted O(R - L) calculation time, so whole recursion will be
I don't remember exactly how do we make it run in O(1) from this point, but should be possible with some bit manipulation.
Here's the solution in :
:
Note that you can do it like on a segment tree now, when you are in some node [L;R] and want to process interval [A;B] you need to either answer the query instantly if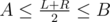 or whole interval [A;B] is in
or whole interval [A;B] is in 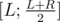 or
or 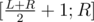 so you can move here to answer query thus having O(h) time complexity, where h is
so you can move here to answer query thus having O(h) time complexity, where h is 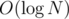
It is obvious that M that we are looking for must be such that A <= M <= B. Thus, it is obvious that leading bits these are equal in A and B must remain same in M. It it also obvious that if we were starting our recursion with L = 0 and R = 2 ^ k — 1, then M such that it has whole equal prefix of A and B with a single 1-bit right afterwards in the position where L and R were split in the first place.
I don't remember the exact O(1) formula to get that value though. :[
Hope this helps you!
if anyone has any doubt regarding the implementation of the above method can refer this: https://discuss.codechef.com/questions/116992/disjoint-sparse-table
Along with O(logN) solution , it also discuss an O(1) solution. We however cant update it. It can replace segment tree if no updates are required.
Hope this helps!! Thank you!!
There is a simple way of getting table for inverse of factorials partially avoiding inverse calculation. If you have n! - 1 then (n - 1) - 1 = n! - 1·n. n! - 1 can be either precalculated or calculated the normal way if you want O(n + q) instead of O(n + qlogn). I think there was some other method of calculating inverse for all numbers from 1 to n or their factorials in O(n) but it required a bit more of number theory knowledge to understand and I can't remember it.
If mod is not very big, you can do it in time where M = mod.
time where M = mod.
Here's link, but unfortunately it's only in Russian.
If (a < b) answer is 0, if (a == b) answer is (1 % MOD), otherwise Product(b+1, a) % MOD
Imagine you have number A, module M, and remainder C:
Now you need a multiplication loop (b .. a] taking module on every step
if(a < b) answer isn't zero.
For example, 5!/6!(mod 1e9+7) = 36166666920
Sorry, than what does the exclamation sign means here? I thought that it's factorial:
120 / 720 is not 0.
It's not 0, but mathematical modulo operation is applicable only for integer division, so the answer must be integer
By the way, in the condition, I think, that 'a' is meant to be 'n', and 'b' is meant to be 'm'. So there is a rule, that 1 <= m <= n, and (a < b) can be a valid input
I gave a wrong answer! Sorry
I don't get what Euler's Phi has to do with that, it's Fermat's theorem which has. And this works only if mod is prime.
Corrected, u are right.. Used the word phi by mistake
and the word Euler
...