Thanks to all the participants for successful submissions!
This set has been prepared by snarknews, Chmel_Tolstiy, Gassa and Zlobober. The analysis was prepared by snarknews and Gassa.
Problem А. Alphabetical E-mail
Note that sets of vowels and consonants does not intersect, which means that, when comparing two subsequences lexicographically, first goes the one with the lesser first letter.
So read the characters one by one and remember first consonant and first vowel. When we meet both of them, immediately compare and print the answer. One of the subsequences can be empty.
Problem B. Bytaler
Read the first exchange rate and set 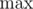 and
and 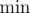 to its value. Then read all other exchange rates; if the next rate is greater than
to its value. Then read all other exchange rates; if the next rate is greater than 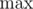 , then set
, then set 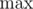 to it, and if it is less than
to it, and if it is less than 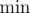 , set
, set 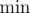 to it.
to it.
Answer will be  .
.
Problem C. Chesskers
Because black checker can make no more than 7 turns before it will reach the 1st rank (or be removed by a white knight), and the white knight can also make no more than 7 turns (even if white move first, after seventh turn, the black checker reaches rank 1 and wins). Note that, at each turn, the checker has no more than 2 possibilities to move, and knight has not more than 8 possibilities, so we will have not more than 27·87 = 228 operations, which is small enough to just solve the problem recursively.
Let us implement two functions:
Checker's turn function which checks winning/losing condition, and if they are not reached, call the functions of knight's turn for all possible checker's moves.
Knight's turn function which checks winning/losing condition, and if they are not reached, call the functions of checker's turn for all (no more than eight) possible knight's moves.
So, the main procedure reads the input data, and then calls the appropriate function depending on who starts the game.
Problem D. Desert City
Consider the diagonal AC of the convex pentagon. Two vertices (let us call them D and E) are lying at one side of it, and one (let us call it B) on another, so we have two diagonals BD and BE intersecting AC in inner points P and Q. Diagonals AD and CE are diagonals of a convex quadrilateral ACDE, so they intersect inside this quadrilateral. Diagonals BE and AD intersect inside the ACDE too (otherwise, we have segment EQ which connects vertice E of a convex quadrilateral ACDE with point Q on AC and does not intersect diagonal AD, which is impossible). The same is true for BD and CE. So, the three other intersection points are lying at one side of the line AC, connecting points P and Q. This means that intersections of diagonals of the convex pentagon form another convex pentagon PQRST with parts of diagonals as its edges.
In this case, vertices of the pentagon ABCDE can be reconstructed as the intersections of the lines which contain the pairs of sides which don't share a vertex (let us say these are PQ and RS). First, PQ and RS cannot be parallel. Also, because ABCDE is convex and edges of PQRST are parts of its diagonals, intersection must lie at another side of line QR than the other vertices of PQRST. So, if this is true for all five pairs of lines, then the convex pentagon ABCDE can be reconstructed correctly.
Taking all the above into account, the following solution can be considered We check if all five given points are vertices of their convex hull, then reorder them so that the pentagon A0A1A2A3A4 is convex, then check for each i if AiAi + 1 and Ai + 2Ai + 3 intersect at some point Qi which lies at the other side of Ai + 1Ai + 2 than Ai (here, the sum in indices is calculated modulo 5). If any of the checks failed, the answer is No. Otherwise, the answer is Yes.
Problem E. Encoding
If it is impossible to select such a pair of p and q, then f(x) is permutation polynomial modulo 2m, which means that it transforms the sequence of consecutive integers from 0 to 2m - 1 into their permutation. Below, we show certain properties of permutation polynomials.
It is easy to see that for m = 1 and for any permutation polynomial, the sum a1 + ... + an must be odd: f(0) = a0 and f(1) = a0 + (a1 + ... + an); so if a1 + ... + an is even, then f(0) = f(1) modulo 2.
If m > 1, then a1 for permutation polynomial must be odd. Otherwise, f(2m - 1) - f(0) = a0 + a1·2m - 1 + 22m - 2·R - a0, where R is an integer. Now, if a1 is even, then f(2m - 1) - f(0) = 2m·(a1 / 2 + 2m - 2·R), so f(2m - 1) - f(0) is divisible by 2m.
After some more experiments you may notice the following rule: if a polynomial is a permutation polynomial modulo 2m, this polynomial also must have even sum a3 + a5 + ... and even sum a2 + a4 + .... Proof of this theorem can be found, for example, in this paper by Ronald L. Rivest.
So, all you need is to check that the sum a1 + a2 + a3 + ... + an is even, and if m > 1, additionally check that a1 is odd and the sum a2 + a4 + ... is even. If this is true, the answer is No (the input contains a permutation polynomial). Otherwise, the answer is Yes.
Problem F. Future Playlists
At first step, we should find a set K of vertices that belong to a single strongly connected component such that there is no edge that starts in a vertex from this set and ends in a vertex outside it.
Due to restrictions from the, problem statement it is possible to find such set, this set is unique, and the vertex corresponding to Byteasar's favorite track belongs to this set.
To find this set, we can run a depth-first search from vertex 1.
It is obvious that at 102016-th track, the probabilities for playing tracks not in our set can be considered as zeroes; moreover, 102016 in this problem can be considered as infinity.
After an infinite number of rounds, the vector p of probabilities must conform to linear equation system pW = p, where W is the adjacency matrix of the subgraph built from vertices of the set K.
So we have a homoheneous system of linear equations (WT - I)pT = 0, and an additional equation 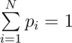 . It is easy to see that system is consistent and it can be solved, for example, by Gaussian elimination.
. It is easy to see that system is consistent and it can be solved, for example, by Gaussian elimination.
The value p1 is the answer.
P.S. If you find a typo, let me know with a private message.










Auto comment: topic has been translated by Chmel_Tolstiy (original revision, translated revision, compare)
Auto comment: topic has been updated by Chmel_Tolstiy (previous revision, new revision, compare).