The problem is that we need to put sum of all individual sub arrays in an array, and sort the array. Then there are at most 20 queries of the form [L, R], we need to report the sum between the indices L and R in the sorted array.
Here is the link.
| # | User | Rating |
|---|---|---|
| 1 | tourist | 3880 |
| 2 | jiangly | 3669 |
| 3 | ecnerwala | 3654 |
| 4 | Benq | 3627 |
| 5 | orzdevinwang | 3612 |
| 6 | Geothermal | 3569 |
| 6 | cnnfls_csy | 3569 |
| 8 | jqdai0815 | 3532 |
| 9 | Radewoosh | 3522 |
| 10 | gyh20 | 3447 |
| # | User | Contrib. |
|---|---|---|
| 1 | awoo | 161 |
| 2 | maomao90 | 160 |
| 3 | adamant | 156 |
| 4 | maroonrk | 153 |
| 5 | -is-this-fft- | 148 |
| 5 | atcoder_official | 148 |
| 5 | SecondThread | 148 |
| 8 | Petr | 147 |
| 9 | nor | 144 |
| 9 | TheScrasse | 144 |
The problem is that we need to put sum of all individual sub arrays in an array, and sort the array. Then there are at most 20 queries of the form [L, R], we need to report the sum between the indices L and R in the sorted array.
Here is the link.
| Name |
|---|



Maybe the following approach is fast enough. It's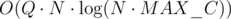 .
.
Codechef should hire someone to check the statements before the contest (typos and other mistakes).
What should I do in cases where the sum-array has repeated numbers?
Example: [1, 1, 1, 1, 2, 2, 2, 3, 3] (obtained when the original array is [1, 1, 1, 1]). If L = 2 and R = 6, v1 will be 1 and v2 will be 2, so the third step would give as result the sum of every element whose value is in interval [1, 2], i.e. 10, while the correct result should be 7.
TL;DR
Find c — the number of intervals smaller than v1. From the sum of sums in interval [v1, v2] you must subtract (L - 1 - c)·v1 because we shouldn't have summed L - 1 - c sums equal to v1. Do the same from the right for R. In case it isn't clear what to do, read much more detailed description below.
First, let me give you a useful advice. To avoid copy-pasting or writing similar thing twice, at the begging you should change problem from
- "find the sum of elements from L to R"
into
- "for given X find the sum of elements from 1 to X"
and then print f(X = R) - f(X = L - 1). It's very standard trick and allows to avoid mistakes.
Now, we are given some X and the task is to sum up smallest X sums. We binary search the value of the X-th smallest sum (as I described in the first post). Let v denote this value. With two pointers we can find the following values:
The answer is S + (X - c)·v. I will explain why. In the sorted array of size N·(N + 1) / 2 we summed up first c elements (smaller than v) and just after them there are some elements equal to v. We must add X - c of them (because we already summed first c but we need first X elements).