const int *
int const *
int * const
int const * const
const int * function (const arg) const
return void(l = r = 0);
VERSION 2.0 RELEASED! Now with 100% less memory leaks or MLE verdicts. Project moved from Github.
The following text is for version 1.0.
Based on the e-maxx implementation and other stuff I found online, I pieced together a powerful treap. It can be used as a set<>, array, segment tree or (within limits) all of them at once.
Consider a set<> represented as a sorted array of distinct elements. You can insert/remove elements just like in a set<>. You can also find the index of any element in this array, remove an element by index — or insert an element at an index, but that will probably break the sortedness and you can't use the operations which rely on it anymore (you can still insert/remove elements by index). As long as the array is sorted, you can query lower bound / upper bound of any element, given as a pair (element, index).
Next, you can reverse a range, add to a range and query range sums; this will work all the time, but range addition can and reversing will break the sortedness. You can implement your own queries (like min/max) or combined range updates (paint+add) like in a segment tree. Since we need lazy propagation, everything is immutable (you can work around it e.g. with erase/insert) and I decided not to bother with iterators.
I took special care with randomisation. It uses testlib random_t and if equal priorities are detected (at insert), they're all regenerated, but it shouldn't happen with reasonably small data — the priorities are 60-bit, which is far above the Birthday Paradox threshold for just about anything.
The DS is templated over some type T, which has to be comparable and support addition / subtraction / multiplication by int (like a vector space in math).
It supports the following operations, all online in 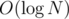 (with N being the current number of elements, ofc):
(with N being the current number of elements, ofc):
| function | action | returns |
| insert(element) | inserts element into a set | bool(was it inserted?) |
| insert_pos(index, element) | inserts element at index | void |
| erase(element) | removes element from a set | bool(was it removed?) |
| erase_pos(index) | removes element at index | void |
| get_index(element) | finds the element's index, size() if non-existent | int in [0..size()] |
| [index] | finds the element at index | T (not T&) |
| lower_bound(element) | finds the lower_bound() of that element, with index | pair<T,int> |
| upper_bound(element) | the same with upper_bound() | pair<T,int> |
| shift(left,right,element) | add element to everything in the range [left,right] | void |
| reverse(left,right) | reverse the range [left,right] | void |
| sum(left,right) | find the sum of the range [left,right] | T |
Also, there's the usual empty(), size(), is_sorted() (returns true if the sortedness hasn't been broken yet) and srand(), which lets you choose your seed if you don't want the testlib default.
I compared it with STL set<> on a million insert/erase/lower_bound operations; the treapset is ~3-4 times slower (which makes sense, since the structure supports many more operations). I also tested it on a million insert_pos/get_index/shift/reverse/sum operations; it took ~4 seconds locally. It seems to work...











Some questions. What happens if there is no element at the position? (erase_pos). Similarly, what happens if you insert_pos at position 273472348, or something? Does it default to the size of the set?
nothing, if(pos >= s.size()) return;
Wow! This is so cool
I have got MLE here https://codeforces.com/contest/641/submission/189834153
all my code is
Maybe not all bugs were fixed or am I doing something wrong?
Didn't check your code yet but not all bugs were fixed. I know about it from some older submission but didn't get to it.
205220953 Took me a while to get to it, but here it works. What happened: there are memory leaks I'm just fixing, but you ran out of memory for an unrelated reason.
The real problem isn't a bug, it's by design — you have to choose RNG properly since the default became "allocate your own RNG" and that's a big object, which isn't a problem unless you're making potentially 200,000 of them like here. The non-default (but somewhat recommended) alternative is choosing your own RNG, in this case one for the whole program is sufficient:
I'll have to put proper info in the readme.