Disclaimer: Maybe I'm totally blind and this is already possible.
There's a lot of contests by now and scrolling through the pages is more annoying. Imagine you're looking for stuff from some div1-rated contest. The contest list is full of div2+ and educational rounds, plus some rare April Fools contest and such. How about a simple filter:
- show only contests rated for selected divisions, or unrated — this is the most important part
- only educational/hide educational
- only sponsored contests
- only team (remember 2-person team VK Cup?) contests
As a bonus, this will let you see a nice unbroken line of green in the "solved" column without having to try solving problems from contests not relevant for you. If you practiced properly.










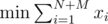
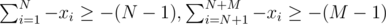
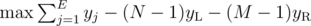
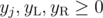
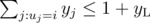 (sum over edges incident on vertex
(sum over edges incident on vertex 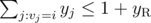 (same as above for the right part)
(same as above for the right part) are assigned to the left and right part of the graph and if they're fixed, finding the optimal
are assigned to the left and right part of the graph and if they're fixed, finding the optimal  for example for an almost complete bipartite graph
for example for an almost complete bipartite graph 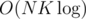 gets TLE for the 5th subtask and even
gets TLE for the 5th subtask and even 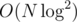 solution isn't hard, but improving it enough to get more points is; 93pts
solution isn't hard, but improving it enough to get more points is; 93pts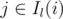 and
and 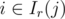 ? This can be solved e.g. using another RMQ table, in which we'll store the minimum left ends of
? This can be solved e.g. using another RMQ table, in which we'll store the minimum left ends of 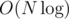 in total.
in total.
 (with
(with 


 is better.
is better.

 , then the train can take it and wait in town
, then the train can take it and wait in town 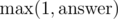 ; since the answer is
; since the answer is 
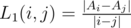 for
for 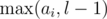 and
and 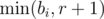 . The number of those subarrays is
. The number of those subarrays is 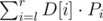 . We only need to precompute all
. We only need to precompute all  time.
time.
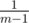 . The expected values are sums with probabilities
. The expected values are sums with probabilities 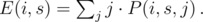
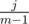 , we know that with probability
, we know that with probability 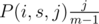 , we had
, we had 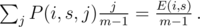
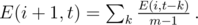
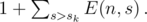

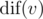 for just one fixed
for just one fixed 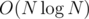 . The time complexity is therefore
. The time complexity is therefore 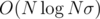 . However, the same is true for the memory, so you can't waste it too much!
. However, the same is true for the memory, so you can't waste it too much! . Count the number of distinct strings which occurred exactly
. Count the number of distinct strings which occurred exactly 
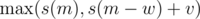 ; the right way to do it is in decreasing order of
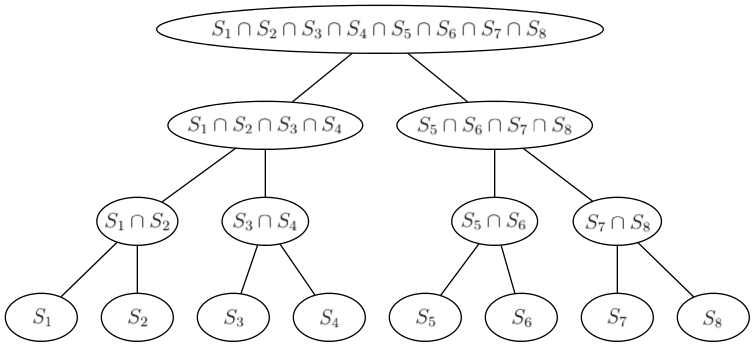
; the right way to do it is in decreasing order of  — the intersections of pairs of queries
— the intersections of pairs of queries  and the time complexity is
and the time complexity is 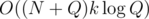 .
.
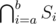 for some
for some 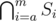 or
or 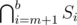 for
for 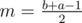 (depending on whether it's the left or the right son). In the first case, only elements removed between the
(depending on whether it's the left or the right son). In the first case, only elements removed between the 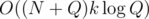 .
.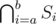 , we can remember for each exhibit the interval of time when it was displayed. The exhibit is in the set
, we can remember for each exhibit the interval of time when it was displayed. The exhibit is in the set 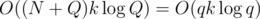 and since we don't need to remember all levels of the perfect binary tree, but just the one we're computing and the one above it, the memory complexity is
and since we don't need to remember all levels of the perfect binary tree, but just the one we're computing and the one above it, the memory complexity is 

