Hints:
div2A: Try conversions between bases.
div2B: Solve a simpler version of the problem where Ai + 1 ≠ Ai for all i.
div1A: What are the shortest paths of the vehicles? what's the shorter of those paths?
div1B: Forget about the ceiling function. Draw points (i, A[i]) and lines between them — what's the Lipschitz constant geometrically?
div1C: Some dynamic programming. Definitely not for the exp. score of one person — look at fixed scores instead.
div1D: Compute dif(v) in O(N) (without hashing) and then solve the problem in O(N2). You need some smart merges.
div1E: Can you solve the problem without events of type 1 or 2? Also, how about solving it offline — as queries on subsets.

Div. 2 A: Two Bases
It's easy to compare two numbers if the same base belong to both. And our numbers can be converted to a common base — just use the formulas
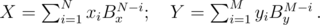
A straightforward implementation takes O(N + M) time and memory. Watch out, you need 64-bit integers! And don't use pow — iterating 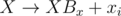 is better.
is better.
Div. 2 B: Approximating a Constant Range
Let's process the numbers from left to right and recompute the longest range ending at the currently processed number.
One option would be remembering the last position of each integer using STL map<>/set<> data structures, looking at the first occurrences of Ai plus/minus 1 or 2 to the left of the current Ai and deciding on the almost constant range ending at Ai based on the second closest of those numbers.
However, there's a simpler and more efficient option — notice that if we look at non-zero differences in any almost constant range, then they must alternate: .., + 1, - 1, + 1, - 1, ... If there were two successive differences of
Unable to parse markup [type=CF_TEX]
-s or - 1-s (possibly separated by some differences of 0), then we'd have numbers a - 1, a, a, ..., a, a + 1, so a range that contains them isn't almost constant.Let's remember the latest non-zero difference (whether it was +1 or -1 and where it happened); it's easy to update this info when encountering a new non-zero difference.
When doing that update, we should also check whether the new non-zero difference is the same as the latest one (if Ai - Ai - 1 = Aj + 1 - Aj). If it is, then we know that any almost constant range that contains Ai can't contain Aj. Therefore, we can keep the current leftmost endpoint l of a constant range and update it to j + 1 in any such situation; the length of the longest almost constant range ending at Ai will be i - l + 1.
This only needs a constant number of operations per each Ai, so the time complexity is O(N). Memory: O(N), but it can be implemented in O(1).
Bonus: the maximum difference permitted in an almost constant range is an arbitrary D.

Div. 2 C / Div. 1 A: The Two Routes
The condition that the train and bus can't meet at one vertex except the final one is just trolling. If there's a railway  , then the train can take it and wait in town N. If there's no such railway, then there's a road
, then the train can take it and wait in town N. If there's no such railway, then there's a road  , the bus can take it and wait in N instead. There's nothing forbidding this :D.
, the bus can take it and wait in N instead. There's nothing forbidding this :D.
The route of one vehicle is clear. How about the other one? Well, it can move as it wants, so the answer is the length of its shortest path from 1 to N... or - 1 if no such path exists. It can be found by BFS in time O(N + M) = O(N2).
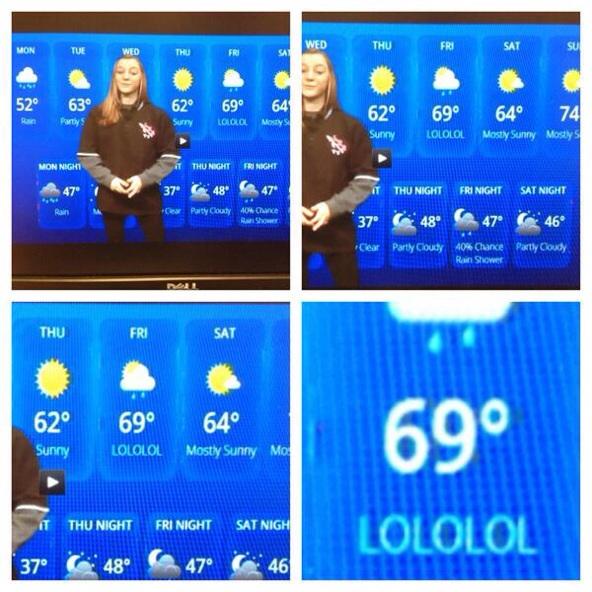
In order to avoid casework, we can just compute the answer as the maximum of the train's and the bus's shortest distance from 1 to N. That way, we compute  ; since the answer is ≥ 1, it works well.
; since the answer is ≥ 1, it works well.
In summary, time and memory complexity: O(N2).
Bonus: Assume that there are
Unable to parse markup [type=CF_TEX]
roads and M2 railways given on the input, all of them pairwise distinct.Bonus 2: Additionally, assume that the edges are weighted. The speed of both vehicles is still the same — traversing an edge of length l takes l hours.
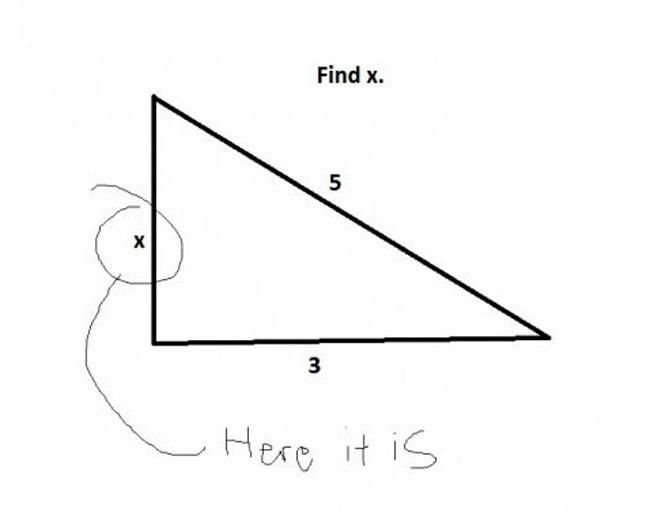
Div. 2 D / Div. 1 B: Lipshitz Sequence
Let 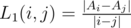 for i ≠ j.
for i ≠ j.
Key observation: it's sufficient to consider j = i + 1 when calculating the Lipschitz constant. It can be seen if you draw points (i, Ai) and lines between them on paper — the steepest lines must be between adjacent pairs of points.
In order to prove it properly, we'll consider three numbers Ai, Aj, Ak (i < j < k) and show that one of the numbers L1(i, j), L1(j, k) is ≥ L1(i, k). W.l.o.g., we may assume Ai ≤ Ak. There are 3 cases depending on the position of Aj relative to Ai, Ak:
Aj > Ai, Ak — we can see that L1(i, j) > L1(i, k), since |Aj - Ai| = Aj - Ai > Ak - Ai = |Ak - Ai| and j - i < k - i; we just need to divide those inequalities
Aj < Ai, Ak — this is similar to the previous case, we can prove that L1(j, k) > L1(i, k) in the same way
Ai ≤ Aj ≤ Ak — this case requires more work:
- we'll denote d1y = Aj - Ai, d2y = Ak - Aj, d1x = j - i, d2x = k - j
- then, L1(i, j) = d1y / d1x, L1(j, k) = d2y / d2x, L1(i, k) = (d1y + d2y) / (d1x + d2x)
- let's prove it by contradiction: assume that L1(i, j), L1(j, k) < L1(i, k)
- d1y + d2y = L1(i, j)d1x + L1(j, k)d2x < L1(i, k)d1x + L1(i, k)d2x = L1(i, k)(d1x + d2x) = d1y + d2y, which is a contradiction
We've just proved that to any L1 computed for two elements A[i], A[k] with k > i + 1, we can replace one of i, j by a point j between them without decreasing L1; a sufficient amount of such operations will give us k = i + 1. Therefore, the max. L1 can be found by only considering differences between adjacent points.
This is actually a huge simplification — the Lipschitz constant of an array is the maximum abs. difference of adjacent elements! If we replace the array A[1..n] by an array D[1..n - 1] of differences, D[i] = A[i + 1] - A[i], then the Lipschitz constant of a subarray A[l, r] is the max. element in the subarray D[l..r - 1]. Finding subarray maxima actually sounds quite standard, doesn't it?
No segment trees, of course — there are still too many subarrays to consider.
So, what do we do next? There are queries to answer, but not too many of them, so we can process each of them in O(N) time. One approach that works is assigning a max. difference D[i] to each subarray — since there can be multiple max. D[i], let's take the leftmost one.
We can invert it to determine the subarrays for which a given D[i] is maximum: if D[ai] is the closest difference to the left of D[i] that's ≥ D[i] or ai = 0 if there's none, and D[bi] is the closest difference to the right that's > D[i] or bi = n - 1 if there's none (note the strict/non-strict inequality signs — we don't care about differences equal to D[i] to its right, but there can't be any to its left, or it wouldn't be the leftmost max.), then those are all subarrays D[j..k] such that ai < j ≤ i ≤ k < bi.
If we don't have the whole array D[1..n - 1], but only some subarray D[l..r], then we can simply replace ai by 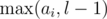 and bi by
and bi by 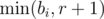 . The number of those subarrays is Pi = (i - ai)(bi - i), since we can choose j and k independently.
. The number of those subarrays is Pi = (i - ai)(bi - i), since we can choose j and k independently.
All we have to do to answer a query is check all differences, take ai, bi (as the max/min with some precomputed values) and compute Pi; the answer to the query is 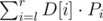 . We only need to precompute all ai, bi for the whole array D[1..n - 1] now; that's a standard problem, solvable using stacks in O(N) time or using maps + Fenwick trees in
. We only need to precompute all ai, bi for the whole array D[1..n - 1] now; that's a standard problem, solvable using stacks in O(N) time or using maps + Fenwick trees in  time.
time.
The total time complexity is O(NQ), memory O(N).
Bonus: Q ≤ 105.

Div. 1 C: Kleofáš and the n-thlon
As it usually happens with computing expected values, the solution is dynamic programming. There are 2 things we could try to compute: probabilities of individual overall ranks of Kleofáš or just some expected values. In this case, the latter option works.
- "one bit is 8 bytes?"
- "no, the other way around"
- "so 8 bytes is 1 bit?"
After some attempts, one finds out that there's no reasonable way to make a DP for an expected rank or score of one person (or multiple people). What does work, and will be the basis of our solution, is the exact opposite: we can compute the expected number of people with a given score. The most obvious DP for it would compute E(i, s) — the exp. number of people other than Kleofáš with score s after the first i competitions.
Initially, E(0, 0) = m - 1 and E(0, s > 0) = 0. How can we get someone with score s in competition i? That person can have any score k from 1 to m except xi (since Kleofáš has that one) with the same probability 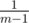 . The expected values are sums with probabilities P(i, s, j) that there are j people with score s:
. The expected values are sums with probabilities P(i, s, j) that there are j people with score s:
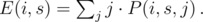
Considering that the probability that one of them will get score k is 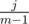 , we know that with probability
, we know that with probability 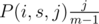 , we had j people with score s before the competition and one of them had score s + k after that competition — adding 1 to E(i + 1, s + k). By summation over j, we'll find the exp. number of people who had overall score s and scored k more:
, we had j people with score s before the competition and one of them had score s + k after that competition — adding 1 to E(i + 1, s + k). By summation over j, we'll find the exp. number of people who had overall score s and scored k more:
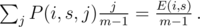
Lol, it turns out to be so simple.
We can find the probability E(i + 1, t) afterwards: since getting overall score t after i + 1 competitions means getting score k in the currently processed competition and overall score s = t - k before, and both distinct k and expectations for people with distinct s are totally independent of each other, then we just need to sum up the exp. numbers of people with those scores (which we just computed) over the allowed k:
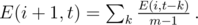
The formulas for our DP are now complete and we can use them to compute E(n, s) for all 1 ≤ s ≤ mn. Since E(n, s) people with s greater than the overall score sk of Kleofáš add E(n, s) to the overall rank of Kleofáš and people with s ≤ sk add nothing, we can find the answer as
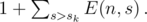
This takes O(m2n2) time, since there are O(mn) scores, O(mn2) states of the DP and directly computing each of them takes O(m) time. Too slow.
We can do better, of course. Let's forget about dividing by m - 1 for a while; then, E(i + 1, t) is a sum of E(i, s) for one or two ranges of scores — or for one range minus one value. If you can solve div1C, then you should immediately know what to do: compute prefix sums of E(i, s) over s and find E(i + 1, t) for each t using them.
And now, computing one state takes O(1) time and the problem is solved in O(mn2) time (and memory).
Bonus: Really, how fast can you solve this problem?

Div. 1 D: Acyclic Organic Compounds
The name is really almost unrelated — it's just what a tree with arbitrary letters typically is in chemistry.
If you solved problem TREEPATH from the recent Codechef November Challenge, this problem should be easier for you — it uses the same technique, after all.
Let's figure out how to compute 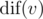 for just one fixed v. One more or less obvious way is computing hashes of our strings in a DFS and then counting the number of distinct hashes (which is why there are anti-hash tests :D). However, there's another, deterministic and faster way.
for just one fixed v. One more or less obvious way is computing hashes of our strings in a DFS and then counting the number of distinct hashes (which is why there are anti-hash tests :D). However, there's another, deterministic and faster way.
Compressing the subtree Tv into a trie.
Recall that a trie is a rooted tree with a letter in each vertex (or possibly nothing in the root), where each vertex encodes a unique string read along the path from the root to it; it has at most σ sons, where σ = 26 is the size of the alphabet, and each son contains a different letter. Adding a son is done trivially in O(σ) (each vertex contains an array of 26 links to — possibly non-existent — sons) and moving down to a son with the character c is then possible in O(1).
Compressing a subtree can be done in a DFS. Let's build a trie Hv (because Tv is already used), initially consisting only of one vertex — the root containing the letter sv. In the DFS, we'll remember the current vertex R of the tree T and the current vertex cur of the trie. We'll start the DFS at v with cur being the root of Hv; all we need to do is look at each son S of R in DFS, create the son curs of cur corresponding to the character sS (if it didn't exist yet) and run DFS(S, curs). This DFS does nothing but construct Hv that encodes all strings read down from v in Tv. And since each vertex of Hv encodes a distinct string, 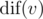 is the number of vertices of Hv.
is the number of vertices of Hv.
This runs in O(|Tv|σ) time, since it can create a trie with |Tv| vertices in the worst case. Overall, it'd be O(N2σ) if T looks sufficiently like a path.
The HLD trick
Well, what can we do to improve it? This trick is really the same — find the son w of v that has the maximum |Tw|, add sv to Hw and make it Hv; then, DFS through the rest of Tv and complete the trie Hv as in the slow solution. The trick resembles HLD a lot, since we're basically remembering tries on HLD-paths.
If v is a leaf, of course, we can just create Hv that consists of one vertex.
How do we "add" v to a trie Hw of its son w? Well, v should be the root of the trie afterwards and the original Hw's root should become its son, so we're rerooting Hw. We'll just create a new vertex in Hw with sv in it, make it the root of Hw and make the previous root of Hw its son. And if we number the tries somehow, then we can just set the number of Hv to be the number of Hw.
It remains true that dif(v) is |Hv| — the number of vertices in the trie Hv, which allows us to compute those values directly. After computing dif(v) for each v, we can just compute both statistics directly in O(N).
Since each vertex of T corresponds to vertices in at most  tries (for each heavy edge that's on the path from it to the root), we aren't creating tries with a total of O(N2) vertices, but
tries (for each heavy edge that's on the path from it to the root), we aren't creating tries with a total of O(N2) vertices, but 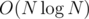 . The time complexity is therefore
. The time complexity is therefore 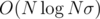 . However, the same is true for the memory, so you can't waste it too much!
. However, the same is true for the memory, so you can't waste it too much!
Bonus: you have an additional tiebreaker condition for vertices with identical  . Count the number of distinct strings which occurred exactly k times for each k in an array Pr[]; take the vertex/vertices with lexicograhically maximum Pr[] (as many strings as possible which occur only once, etc).
. Count the number of distinct strings which occurred exactly k times for each k in an array Pr[]; take the vertex/vertices with lexicograhically maximum Pr[] (as many strings as possible which occur only once, etc).
Bonus 2: Can you get rid of the logarithm in the time complexity?

Comic strip name: Indy. Go read the whole thing, it's not very long, but pretty good.
Div. 1 E: A Museum Robbery
In this problem, we are supposed to solve the 0-1 knapsack problem for a set of items which changes over time. We'll solve it offline — each query (event of type 3) is asked about a subset of all N exhibits appearing on the input.
Introduction
If we just had 1 query and nothing else, it's just standard knapsack DP. We'll add the exhibits one by one and update s(m) (initially, s(m) = 0 for all m). When processing an exhibit with (v, w), in order to get loot with mass m, we can either take that exhibit and get value at least s(m - w) + v, or not take it and get s(m); therefore, we need to replace s(m) by 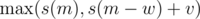 ; the right way to do it is in decreasing order of m.
; the right way to do it is in decreasing order of m.
In fact, it's possible to merge 2 knapsacks with any number of items in O(k2), but that's not what we want here.
Note that we can add exhibits this way. Thus, if there were no queries of type 2, we would be able to solve whole problem in O(Nk) time by just remembering the current s(m) and updating it when adding an exhibit. Even if all queries were of type 2 (with larger n), we'd be able to solve it in O(nk) time in a similar way after sorting the exhibits in the order of their removal and processing queries/removals in reverse chronological order.
The key
Let's have q queries numbered 1 through Q in the order in which they're asked; query q is asked on some subset Sq of exhibits.
MAGIC TRICK: Compute the values s(m) only for subsets  — the intersections of pairs of queries 2q, 2q + 1 (intersection of the first and the second query, of the third and fourth etc.), recursively. Then, recompute s(m) for all individual queries in O((N + Q)k) time by adding elements which are missing in the intersection, using the standard knapsack method.
— the intersections of pairs of queries 2q, 2q + 1 (intersection of the first and the second query, of the third and fourth etc.), recursively. Then, recompute s(m) for all individual queries in O((N + Q)k) time by adding elements which are missing in the intersection, using the standard knapsack method.
What?! How does this work?! Shouldn't it be more like O(N2) time? Well, no — just look at one exhibit and the queries where it appears. It'll be a contiguous range of them — since it's displayed until it's removed (or the events end). This element will only be missing in the intersection, but present in one query (so it'll be one of the elements added using knapsack DP), if query 2q + 1 is the one where it appears first or query 2q the one where it appears last. That makes at most two addittions of each element and O(N) over all of them; adding each of them takes O(k) time, which gives O(Nk).
The second part of the complexity, O(Qk) time, is spent by copying the values of s(m) first from the intersection of queries 2q and 2q + 1 to those individual queries.
If we're left with just one query, we can solve it in O(Nk) as the usual 0-1 knapsack.
Since we're halving the number of queries when recursing deeper, we can only recurse to depth 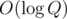 and the time complexity is
and the time complexity is 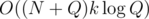 .
.
A different point of view (Baklazan's)
We can also look at this as building a perfect binary tree with sets S1, ..., SQ in leaves and the intersection of sets of children in every other vertex.
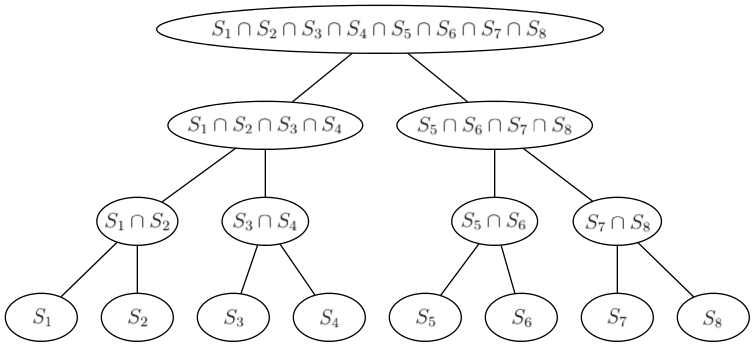
For each vertex v of this tree, we're solving the knapsack — computing s(m) — for the set Dv of displayed exhibits in it. We will solve the knapsack for the root directly and then proceed to the leaves. In each vertex v, we will take s(m), the set Dp of its parent p and find s(m) for v by adding exhibits which are in Dv, but not in Dp.
We know that the set Dp is of the form 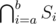 for some a, b and Dv is either of the form
for some a, b and Dv is either of the form 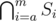 or
or 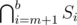 for
for 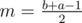 (depending on whether it's the left or the right son). In the first case, only elements removed between the m-th and b-th query have to be added and in the second case, it's only elements added between the a-th and m + 1-th query. Since each element will only be added/removed once and the ranges of queries on the same level of the tree are disjoint, we will do O((N + Q)k) work on each level and the overall time complexity is
(depending on whether it's the left or the right son). In the first case, only elements removed between the m-th and b-th query have to be added and in the second case, it's only elements added between the a-th and m + 1-th query. Since each element will only be added/removed once and the ranges of queries on the same level of the tree are disjoint, we will do O((N + Q)k) work on each level and the overall time complexity is 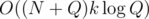 .
.
Finding the intersections and exhibits not in the intersections
Of course, bruteforcing them in O(NQ) isn't such a bad idea, but it'd probably TLE — and we can do better. We've just described how we can pick those exhibits based on the queries between which they were added/removed. Therefore, we can find — for each exhibit — the interval of queries for which it was displayed and remember for each two consecutive queries the elements added and removed between them; finding the exhibits added/removed in some range is then just a matter of iterating over them. Since we're actually adding all of them, this won't worsen the time complexity.
In order to efficiently determine the exhibits in some set 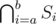 , we can remember for each exhibit the interval of time when it was displayed. The exhibit is in the set
, we can remember for each exhibit the interval of time when it was displayed. The exhibit is in the set 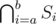 if and only if it was displayed before the a-th query and remained displayed at least until the b-th query.
if and only if it was displayed before the a-th query and remained displayed at least until the b-th query.
To conclude, the time complexity is 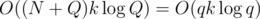 and since we don't need to remember all levels of the perfect binary tree, but just the one we're computing and the one above it, the memory complexity is O(qk).
and since we don't need to remember all levels of the perfect binary tree, but just the one we're computing and the one above it, the memory complexity is O(qk).











You trolled many users. Many would be like what the heck is that?
the best trick i have ever seen. (and also the funniest tags.)
Auto comment: topic has been updated by Xellos (previous revision, new revision, compare).
If I could've upvoted n-times!(n > 1) :)
At least u tried
good trick :D and can dynamic programming solve the bonus?
Yes.
Can you explain how to solve div 2 problem D for Q = 10^5 ? I sense some pre processing would be required...
can you provide the recurrence please ?
Great Contest , I appreciate your effort! I just wanna comment that Div.2/C is easier than Div.2/B for me.
Still I wonder if Div2.C statement did not include the condition each of different pairs is always a rail/road, could we solve it? I was managing to do C with BFS sequentially anyway.
Auto comment: topic has been updated by Xellos (previous revision, new revision, compare).
Now with ∞ percent more images!
You are so generous :) letting O(N^3) pass Div1A and O(N*log^2) pass div1D :)
Another simple solution for div1D (with hashing, although one can get rid of it with a "suffix array on a tree" method).
For each vertex, let h(v) be the polynomial hash of a string from root to v. It can be calculated using one dfs. Easy to notice that number of different strings reachable from some vertex v is exactly the number of different hash values in its subtree, and this is a standard task.
Actually Xellos mentioned that before the suffix explanation. "One more or less obvious way is computing hashes of our strings in a DFS and then counting the number of distinct hashes (which is why there are anti-hash tests :D)." Although evidently the "anti-hash tests" weren't so effective.
Oops, skipped it while reading :( Thank you.
How would you imagine making anti-hash tests for any other large modulo than 264? One modulo close to 109 fails comfortably, but two are practically impossiblt to beat. But it's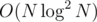 , so it's possible for it to TLE.
, so it's possible for it to TLE.
Oh right. I thought you meant you had general breaking cases for hashing solutions since you seemed so happy when you mentioned them (":D"), which seemed pretty unbelievable to me.
Yes, that would be pretty unbelievable :D
Hashing solutions are provably correct w.h.p. if you pick the prime randomly from a large enough (polynomial-sized) interval, so one can only hope to spoil the fun for some concrete numbers like 1000000007 ;)
Do you know a simple solution for the "standard task" in O(N log N)? My solution was O(N log N) but it was relatively complicated.
You can compress the hash values into the integers from 1 to n and then solve the task "compute the number of different values on [Li, Ri]", where [Li, Ri] is a segment of the Euler tour on a tree.
I don't know what you call "relatively complicated", as your code seems to be really short.
Anyway, an alternative approach is to use the merging technique in which you keep track of all of the hashes present in a subtree, then calculate the hashes present in the parent subtree by merging the results for the children's subtrees. If you always merge by placing elements from the smallest set in the largest set, you can show that the number of jumps each element makes is at most log n, as in 14499298.
A simpler deterministic solution for Div 1 D is to simply merge children with the same letter, so that every node has at most one child of each letter. We can do this recursively and since each node can get merged at most once, the complexity amortizes out.
Code
Div1E's idea is almost the reduction from #319E, did you notice that?
It's also really similar to Good Bye 2014 F
In fact, this problem was really inspired by Good Bye 2014 F. When solving Good Bye 2014, I came up with a solution which was different from the author's one and it also had a different time complexity. So I decided to make a problem, where my approach will still work, but author's solution of Good Bye 2014 F will not.
I think the trick you called "HLD trick" is called smaller-to-greater trick since we're actually using dsu basics.
I've practically never heard of it called "smaller to greater" in any other context than actual DSU (where the notion of HLD-paths is unclear, in addittion).
I don't understand why going so complicated about Div1D. Just build a trie for each node in a dfs, and recursively merge tries for children with equal letters before exiting the node. Total number of nodes in all tries is exactly N, and every merge written in the most straight-forward way takes O(σ), so the total complexity is O(Nσ). Code for reference:
http://codeforces.com/contest/601/submission/14454218
No, merging two tries in the most straightforward way takes O(the sum of their sizes) time. That's why people are complaining about too short editorials on CF :D
No! Every node is merged to some other node not more than once, so the total number of merges is less than N. Of course single recursive call to merge can take linear time, but the total amortized time is still O(Nσ). I wanted to say that merging one node is O(σ) not including recursive calls to merge children.
You said the most straightforward way. That's DFSing fully through both trees.
I know what you mean by your solution, but everything seems much simpler in retrospect. That's why this is not div1B.
I too feel that the way Al.Cash is merging the tries is the most-straightforward way. Doing DFS in each child (except the heavy one) is not more straightforward to think than thinking about simply merge two tries. However, I do agree that realizing that his method will do at-most N merges overall, may not be that straightforward to many.
BTW, my solution is different than both of yours. My idea goes as follows —
- Do dfs and compute hash values for each node for string represented from root (node 0) to that particular node.
- Do pre-order traversal of the tree so that any subtree will appear continuously in the pre-order array.
- Then the problem boils down to find number of distinct numbers in a subarray for a given array (pre-order array), for N such queries.
- This reduced problem can be solved using fenwick tree (see DQUERY ) in (N + Q) log N.
My solution using this Idea — code.I know he's an incurable troll, but I have to side with Xellos in this one. Merging two tries by making a full DFS on the second tree and adding nodes one by one in the first tree is a lot more straightforward than the trick Al.Cash used, by DFSing through both tries simultaneously.
For Div1B, a different solution — O(Q * N log N), just passed for me (873 ms):
Build an array of differences as in the editorial solution, then use a segment tree to find maxima in it. But don't calculate it for each subarray — instead, first just find the index of the greatest element in the entire queried subarray. Calculate the amount this number contributes to the sum with some basic combinatorics, then call a similar query to the two subarrays on the two sides (if they exist) and sum the results. We'll have to find the maximum N times in each query, so it's O(N log N) per query.
This is the solution I used too! Except that instead of Segment Tree I used an RMQ so the complexity becomes O(N log N + Q * N)
I wanted to say I really enjoyed the problemset this time around! D is actually pretty cool — somehow I've never seen merging tries before. After seeing that solution, I mostly wish there was no solution with hashing at all :P
I guess I just am a bit unclear on the purpose of pretests and partial feedback — most major contests don't have them. Is there a blog post anywhere that talks about this?
Pretests are used for two reasons:
Codeforces is nice to you and tells you your solution is dumb so that you can go back and fix it :)
Only solutions that pass pretests can then be hacked, so there are no extra cheap points for just noticing and hacking a dumb submission that doesn't even attempt to solve the correct problem.
And point 3: you can hack others only if your own solution passes pretests. So in order to hack you must write something reasonably clever.
Is it an advantage?
I like problem D, however I am confused because of that statement: "If you solved problem TREEPATH from the recent Codechef November Challenge, this problem should be easier for you — it uses the same technique, after all." I haven't solved that Codechef problem, however setting two similar problems in two different contests at merely the same time and openly admitting to it doesn't seem to be a very good idea (inb4, my judgment is based only on that statement, I haven't read Codechef problem, maybe they are not that similar).
No, they aren't that similar. The Codechef problem is about counting ways to split a tree with a number in each vertex into paths with non-negative sums. It uses a lot more ideas, but the trie compression that's here is not one of them. But the not DFSing through the largest son's vertex is present in both (of course, this can be solved without that with smarter merges as mentioned by Al.Cash above).
I agree that it isn't very good, but neither is just casually making another div1D 3 weeks before the contest just because I'm editorialing something that uses the same technique. And where's the line, then? Should div1E not be used because its solution was made for 500F - Новогодние покупки? Hey, there's probably been a problem that uses probability theory stuff, so div1C isn't suitable either! Nah, that's just not worth it — stuff happens to be similar sometimes, there's just no helping it. It does have a good side, too — if there's an easier and a harder problem using the same trick, then you can practice it more gradually.
As to openly admitting to it, well it is the truth. Why should I act like a politician?
I hate sleep so instead having some I tested this round yesterday. Links to my codes are below, if somebody is interested in them.
I used Dijsktra 4 times in Div2C (Div1A) http://codeforces.com/contest/602/submission/14451579 and my friends said my solution was not only long but also wrong. Was I just lucky this time?
of course instead of writing dijkstra 4 times u can write it once as a function once and call it four times :|
Look how easy it can be done. You don't even need dijkstra, just BFS http://codeforces.com/contest/601/submission/14486558
Why do I get a runtime error all the time for 2A when my code works fine on my system? Here is my code http://ideone.com/Y5g0T8
n1 and n2 are given garbage value by default. You have to first input n1 then define array of size n1. Same applies for n2.
tt
Welcome. :) I see you don't write return 0 in the end this can also sometimes give Runtime Error.
In plain C it can but in C++ it cannot. In C++, if you don't return anything from main, the standard requires the program to terminate with exit code 0.
Didn't know that. Thanks for correction.
It's one of the most detailed editorials I have seen. Awesome!
Problemset was also really good. Congratulations!
why the codes with algorithm O(n*m*log(n)) in problem D(div 1 B) passed system test? I'm wondering how that codes working in 0.6second :\
My code works in 0.12 seconds, so it's really possible. CF is fast.
Div2 B can also be solved using DP:
My submission: 14451702
Brilliant!
Readable solution for problem
div2A:)in div2 C i don't quite understand how not meeting at a node at the same time is meaningless and i noticed people computing only the shortest path for one of the vehicles i used bfs 4 times where i calculate shortest distance for train then car then calculate for car then train and printing minimum
Ehm, either the car or the train can go to town n directly. That way, they won't meet anywhere at the same time.
how i was unable to see that is beyond me thank you
yes, i was also thinking the same,how come it didn't strike my mind that between any two nodes there is either rail or road.Thank you so much
Can you please explain, what logic for this graph would be? Please see screenshot. And what happens in town 4, when bus and train meet there simultaneously? I cannot understand, why they don't meet in 4, if they started from 1 simultaneously. graph screenshot
Your picture is missing a LOT of roads.
Wow! I think I got it now. Thanks, Xellos! That makes it max(1, someBFSResult), right?
Yes.
"In fact, it's possible to merge 2 knapsacks with any number of items in O(k), but that's not what we want here."
How?
typo, O(k2) :D
whats wrong with the library pow function for Div. 2A?
Codeforces + C++ Pow = Error
The pow function works with doubles, and it may generate precision errors in the process.
For Integer powers it's better to use your own power functions!
you can use powl instead of that. my code: 14470229
Using powl will reduce the risk, however it's still a floating point number, so I think it's better to use your own power function for integers
No! powl uses long double and it is good enough for long long.
With long double there won't be overflow if results fit in long long, but there is still chance of getting precision errors.
I prefer to keep on the safe side xP
i solved div 1 B with set and i get tle,however my complexity is O(n log n * q).
Problem Div2-D/Div1-B can be solved using Range Maximum Queries without segment trees.
Given that the elements of the array D will not change, a Sparse Table can be used. This way we can pre-compute the RMQ Sparse Table with complexity O(N*log(N)) and answer RMQ queries in O(1).
Nice problem! ^_^
So,could you give me some hints on div1.B bonus? Thx.
you are creative; thanks for hints!
What is the meaning of anti-hash test when anyone can use triple hash!
(601D - Ациклические органические составляющие)
The purpose of an anti-hash test isn't to break all solutions that use hashing. (In fact, when hashing is used properly, such a solution can even be extremely hard to hack!)
The anti-hash test breaks incorrect implementations of hashing that use hashing modulo 2^32 / 2^64.
Then why sometimes they create an Anti-Hash test for hashes that use 31(as their base) and 109 + 7 (as their Modulo)?
Because they can.
I think you are wrong.The purpose of any kind of input is to break all the breakable codes.If you can break a code uses 1e9+7 as mod, then why not to hack it ?
Could anyone tell me more about problem E div2? I can not understand what tutorial said. Thanks in advance.
Kleofáš's expected rank = 1 + E, where E is the expected number of people who have a smaller score.
By the linearity of expectation:
E = (the number of other people) * P, where P is the probability that Zachariáš (one specific other person) has a smaller score
Let P(s) be the probability that Zachariáš has the score exactly s. P can be computed as the sum of P(s) over all s smaller than Kleofáš's score.
The values P(s) can be computed using dynamic programming.
More precisely, we can compute all values P(s,i): the probability that Zachariáš has score exactly s after i competitions.
This DP can then be computed in a clever way to make the program an order of magnitude faster.
I don't understand the linearity part :(
If P is the probability that some person will get a smaller score than Kleofáš's, how the expected value comes to be (number of other people)*P ?
I'm not very good at probability theory :'(.
Thanks!
Linearity of expectation simply means that if you do two experiments X and Y that each return a random value (e.g., flip a coin and roll a die), the expected value of X+Y is the expected value of X + the expected value of Y. (The nontrivial part is that this is true even if X and Y are not independent.)
This is actually pretty easy to prove. In this problem, we can do it like this.
We will count the same thing twice, using two different methods.
Method 1: Let's take an empty piggy bank. We will now run 1,000,000 n-athlons. After each n-athlon, each person who was better than Kleofáš will put a coin into the piggy bank.
At the end, what is the number of coins in the piggy bank? On average, this should be 1,000,000 * the expected (i.e., average) number of people who are better than Kleofáš.
Method 2: Let's focus on one competitor, Zachariáš. Suppose that he has a better score than Kleofáš with probability p.
What is the number of coins Zachariáš puts into the piggy bank? On average, this should clearly be 1,000,000 * p.
Zachariáš is one of N-1 identical people. Each of these N-1 people will, on average, put 1,000,000 * p coins into the piggy bank.
Both methods are counting the results of the same process. Therefore, it must be the case that the expected number of people who are better than Kleofáš must be (N-1) * p.
I see! Thank you very much! :D
By the way, the fact that the expected value is (n-1)*p could mean that we are dealing with a binomial distribution? Or am I overthinking the problem? :P
I found the answer as the sum over probability of each rank * rank. Probability of given rank(k + 1) =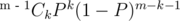 which sums over to
which sums over to 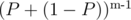 that is 1. The idea behind was that I will choose k which have score lower than sk and rest with score above sk. Something like Bernoulli distribution.
that is 1. The idea behind was that I will choose k which have score lower than sk and rest with score above sk. Something like Bernoulli distribution.
Hi Xellos ! I think in second bullet point in Div. 2 D / Div. 1 B: Lipshitz Sequence instead of "L1(i, j) > L1(j, k)" it should be "L1(j, k) > L1(i, k)"
You're right, thanks.
O(n^2) logic passed in div2 B
include<bits/stdc++.h>
using namespace std; int main() { int n; cin>>n; int a[n]; for( int i=0;i<n;i++) cin>>a[i];
int maxlen=1; int ans=0; for(int i=0;i<n;i++) { int maxi=INT_MIN; int mini=INT_MAX; int count=0; for(int j=i;j<n;j++) { maxi=max(maxi,a[j]); mini=min(mini,a[j]); if(maxi-mini>1) break; count++; } ans=max(count,ans); if(n-i<=ans) break; } cout<<ans <<endl;}
There's a shitload of optimisations, you know. Especially the line
if(n-i<=ans) break;, which cuts down the time for large answers significantly — to O((N - ans)·ans).You forgot to mention those 3 TLE before it and that it takes 1900 ms, though. If the TL wasn't raised to 2 seconds before the round, it'd fail for sure. If someone actually made those optimisations during the round and got lucky enough not to get hacked, it's pretty much deserved.
Can you explain how to solve the bonus problems?
Hi, Can somebody help me with Div1B/Div2D. I am clearly missing out something in this —
Xellos: "One approach that works is assigning a max. difference D[i] to each subarray — since there can be multiple max. D[i], let's take the leftmost one." zodiacLeo: Why the leftmost one ? Even after multiple reads (of the editorial i couldn't get a convincing answer)
Xellos: "We can invert it to determine the subarrays for which a given D[i] is maximum: if D[ai] is the closest difference to the left of D[i] that's ≥ D[i] or ai = 0 if there's none, and D[bi] is the closest difference to the right that's > D[i] or bi = n - 1 if there's none (note the strict/non-strict inequality signs — we don't care about differences equal to D[i] to its right, but there can't be any to its left, or it wouldn't be the leftmost max.), then those are all subarrays D[j..k] such that ai < j ≤ i ≤ k < bi." zodiacLeo: Lost the explanation completely! :|
In my defense, I went through code of misof and mmaxio (both implementation, which I found to be along the lines of the editorial) but still I couldn't get it.
Why not the leftmost one? It doesn't matter which, as long as it's a unique and useful choice.
Do you understand that we need to describe/count the subarrays for which a given difference is maximum? (Because we use it afterwards.)
Try drawing pictures.
I did the drawing part again after what you said, but I am still finding myself in the middle of desert :|. sigh
I guess I'll have to keep probing on such question (involving subarrays etc) which might eventually put my lack of familiarity with subarrays (counting it, describing them, etc) at bay. I'll revisit this problem sometime again in future (hope that's not too far away).
Just for reference - Drawing part
I used the first sample example to understand-
10 4
1 5 2 9 1 3 4 2 1 7
3 8
I haven't uploaded the image where-in I actually run the code (manual tracing/debugging) because it appears nothing more than gibberish.
If you happen to think of a different way to explain this then please do post it over here. (If that's not much to ask already)
That's more of a picture to the original problem, not to the reduced one that you asked about (summing up subarray maxima).
The subproblem we're solving there is "for how many subarrays will D[i] be the leftmost maximum?".
Can some one please help me understand this:
Why don't we have to handle the condition that the bus and train may reach at an intermediate node ( ≠ 1 & ≠ N ) at the same time? Won't there be any possible case such that the bus/train may have to take a longer path, because the shortest path was intersecting with a railway/road ?
What is the shortest path of one of them?
The path obtained by performing BFS from 1 to N, correct?
No. Not in a general shortest path problem. In this problem.
Ok, so as per this:
If this statement means that there is at most one path connecting any 2 towns by railway, then the shortest path of one of them is equal to 1, if such a railway exists.
I have no idea what you're trying to say.
The shortest path of one of the vehicles is the edge from 1 to n. It will always exist, either as a railway or as a road.
I thought about problem (div. 2) D without looking at this editorial first, but the only part I couldn't figure out was the "standard" problem described at the end: the one about precomputing all ai, bi. Do you mind explaining to me how the approach using a stack works?
For example, take this array of consecutive differences: [14, 12, 9, 7, 11, 8]. How would you use a stack to figure out that the latest element before 11 that is ≥ 11 is 12? I went through people's code, but still couldn't figure it out. Thanks for your help!
https://duckduckgo.com/?q=next+greater+element
thanks :D
div2B what am i doing wrong ? my submission :14555108
I also stuck at test 10
Damn. Got trolled in div2C/div1A. :P
I have just solved Div2 B in time O(n) and memory O(1). Also, my solution can be updated to solve this problem with different D (according to bonus task here). I am dividing each element by 2 and using, in one case, floor(), in another — ceil(), next I am counting simillar elements — this is very easy to implemet. My (awful, I know) code: http://codeforces.com/contest/602/submission/15226134 To solve it with different D we need to divide by D+1, I guess.
Xellos: In div2 B, why is checking only for the last position of A[i] + 2 and A[i] -2 enough? What if A[i] + 3 occurs after the last position where A[i] + 2 occurred? Wouldn't the solution be screwed then?
No, because |ai + 1 - ai| ≤ 1. That condition isn't there just for fun.
I think Lipshitz Sequence was good problems not only in terms of graph property but also in terms of stack operation.
I am getting Memory Limit exceeded in test case 57 (Div 1 — A).
I am using an adjacency list instead of an adjacency matrix but how on earth could this be a cause to a MLE ?!!
Any help? A link to my submission: [http://codeforces.com/contest/601/submission/17813603]
I think div1C can be solved O(n) if we didnt have this:
that no two participants are given the same rankam I wrong?Div1 B: Is this test case valid? 6 1 1000000000000000000 0 1000000000000000000 0 1000000000000000000 0 1 6
Ignore...
Ignore...
.