i_love_emilia_clarke's blog

CF 373/Div.2/E — Sasha and Array
By i_love_emilia_clarke, history, 8 years ago, In English

Hi, i was trying to solve this PROBLEM, i am familiar with segment tree and lazy propagation stuff, what i could not see how to perform update operation.

I feel that we need to store the fibonacci sum of segment at each node, or do we need to store something else ? elaborative explanation will be highly appreciated. Thanks in advance.

  • Vote: I like it
  • +1
  • Vote: I do not like it

Comments Comments (3)
| Write comment?
»
8 years ago, # |
← Rev. 2   Vote: I like it 0 Vote: I do not like it

Let F(n) denote the nth Fibonacci number,

then, F(n) can be found by using the following : F(n) = element 0,0 : A*(B^n). where A is a 2x2 matrix : {{1,1},{0,0}} and B is a 2x2 matrix : {{0,1},{1,1}} element 0,0 means the upper left element of the resulting matrix.

Here is the formal equation if you are interested :

{{F(0),F(1)},{0,0}}*({{0,1},{1,1}}^N) = {{F(N),F(N+1)},{0,0}}

so, you can store A*B^k in every node, whenever you get a range update query, update it by multiplying the existing matrix in the node by B^increment.

Hope this helps

→ Reply
»
8 years ago, # |
  Vote: I like it +5 Vote: I do not like it

My method uses Binet's Formula. By Binet's Formula, , where . We can use a custom struct to store number of the form 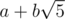. We calculate the answer for α and β separately (on two different segment trees) and then combine them together when we query. Now, each range increment is equivalent to multiplying αk in a range [l, r] and we can find αk using binary exponentiation. (divide and conquer) The rest can be easily handled with a lazy propogation segment tree.

→ Reply
»
8 years ago, # |
  Vote: I like it 0 Vote: I do not like it

I tried the same approach given in the editorial but it's exceeding time limit in test case 11 . What might be the possible reasons Submission. Is it due to excessive creation of matrix objects.

→ Reply