Div2 A. Для решения данной задачи достаточно вывести "0 0 n".
Автор задачи — Alex_KPR .
Div2 B. Для каждой окружности одного кольца нужно определить — имеет ли она пересечения с другим кольцом (касаться можно). Итого 4 проверки.
Возможны 3 случая:
1. окружность внутри кольца;
2. окружность вне кольца и кольцо находится вне окружности;
3. окружность вне кольца и кольцо находится внутри окружности.
Если хотя бы одно из этих условий выполняется, то окружность хорошая.
Проверку легко сделать следующим образом. Пусть d — расстояние между центрами кольца и окружности, r1 и R1 — внутренний и внешний радиусы кольца, r — радиус окружности. Тогда условия запишутся как
1. d + r ≤ r1.
2. r + R1 ≤ d.
3. d + R1 ≤ r.
Эти проверки удобно проводить в целых числах, используя квадраты расстояний.
Автор задачи — Alex_KPR
Div2 C. Div1 A.
Первый вариант решения. Рассмотрим последовательность a0 = 1, ai = ai - 1k + b:
a0, a1, a2, ..., an = z.
Заметим, что для всех чисел из отрезка [a0, a1 - 1] ровно за n преобразований мы получим число не меньше z, однако за n - 1 преобразование мы получим число строго меньше z. Это верно из соображений монотонности функции преобразования. Аналогичные рассуждения можно применить и к числам из отрезков [a1, a2 - 1], [a2, a3 - 1] и так далее, только там будет n - 1, n - 2 шагов и так далее. Значит, для решения задачи, нам нужно узнать к какому из отрезков принадлежит число t. Это можно сделать просто сгенерировав несколько первых членов последовательности a. Не более чем через t шагов найдется подходящий отрезок.
Второй вариант решения. Запишем уравнения в лоб:
tkx + b(kx - 1 + kx - 2... + 1) ≥ kn + b(kx - 1 + kx - 2... + 1)
Воспользуемся формулой для геометрической прогрессии: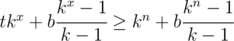
Далее считаем k ≠ 1, случай k = 1 удобно рассмотреть отдельно в самом начале (его разбирать не будем, он тривиален).
t(k - 1)kx + bkx - b ≥ (k - 1)kn + bkn - b
kx(t(k - 1) + b) ≥ kn(k - 1 + b)
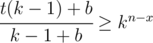
Итак, величину n - x можно найти простым возведением в степень "пока не переполнится".
Div2 D. Div1 B. Заведем граф, в котором вершинами являются участки стен, ребрами — возможные перемещения ниндзя и запустим на нем поиск в ширину (BFS) с одной модификацией: если мы добрались до некоторой вершины позже, чем до туда добралась вода, то оттуда не делаем ходов.
Решение имеет сложность O(n).
Автор — Ripatti
Div2 E. Div1 C. Заметим, что если мы можем достичь планеты за некоторое время t, то мы можем достичь ее и за любое большее время (для этого достаточно достичь ее за время t, а затем просто перемещаться вместе с планетой). Понятно, что существует некоторое t0, для которого для всех t > t0 достичь планету можно, а для всех t < t0 — нельзя. Будем искать t0 при помощи бинпоиска.
Проверку каждого из t внутри бинпоиска можно осуществлять следующим образом. Вычислим положение планеты через время t и найдем расстояние от корабля до этого нового положения.
Задача свелась к следующей "классической" задаче: есть две точки A и B и круг с центром в O радиуса R (точки вне круга), нужно найти расстояние между точками, при этом в круг заходить нельзя.
Возможны 2 случая:
1. Можно пройти напрямую
2. Следует огибать круг
Второй случай выполняется тогда и только тогда, когда верны оба утверждения:
a. Углы OAB и OBA острые
b. Высота OH меньше R
Все проверки можно сделать в целых числах.
Теперь поймем как обработать случаи:
1. Очевидно
2. Пусть C и D — точки касания (т.е. мы должны двигаться по линии ACDB). Треугольники OAC и OBD — прямоугольные, там можно легко вычислить все углы, откуда легко найти угол COD. Дальше вычислить длину линии несложно. Заметим, что находить положения точек C и D совсем не обязательно.
Автор — Ripatti
Div1 D. Суть авторского решения в том, чтобы рекурсивно строить решения в виде параллелепипедов размера k × k × (k + 1), содержащих нужные 2 куба размера k × k × k. Для k = 2 решение очевидно. Далее решение расширятся в соответствии с картинкой:
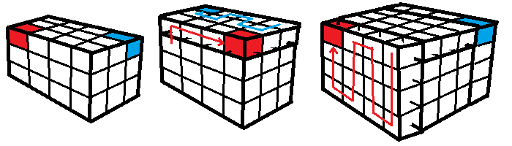
Красный и синий кубики — начало и конец цепи. Сначала мы надстраиваем один этаж сверху, а затем 2 слоя по бокам. Построения зависят от четности текущего k.
Чтобы получить решение для n построим n × n × (n + 1), а потом просто отбросим один слой.
Автор — Ripatti
Div1 E. Расположим все захваты как точки на плоскости с координатами (расстояние, масса). Тогда, пользуясь некоторым захватом, мы можем собирать все захваты внутри некоторого прямоугольника с углом в начале координат. Будем собирать захваты и помещать их в очередь. Тогда для текущего захвата все захваты в прямоугольнике собраны — будем доставать следующий захват из очереди и делать манипуляции с ним. Осталось научиться делать запросы быстро.
Заведем дерево отрезков (например, удобно использовать дерево Фенвика) по координате "расстояние", в каждой вершине которого будем хранить стек из точек, упорядоченных по координате "масса". Каждая вершина дерева отрезков есть некоторый диапазон координат, именно точки из этого диапазона будут храниться в данной вершине. На вершине каждого стека будет захват с наименьшей массой. Положим вначале все точки в это дерево отрезков. Так как каждая координата покрыта не более чем 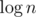 отрезками, всего это дерево будет использовать
отрезками, всего это дерево будет использовать  памяти.
памяти.
При выполнении запроса мы извлекаем из некоторых стеков точки с массой, не превышающей некоторого значения и помещаем их в очередь. Следует отметить, что одна и та же точка может находиться в разных стеках и мы можем случайно положить в очередь одну и ту же точку дважды. Чтобы избежать этого, можно вместе с точкой складывать в дерево отрезков ее номер. А при извлечении точки проверять первое это извлечение или нет в некотором массиве флагов по номеру.
Итого решение имеет сложность  .
.











Спасибо за разбор! Все понятно объяснено.
What does cout<<0<<0 print in prob A div 2.Please explain.
InputThe input contains of a single integer n (0 ≤ n < 10^9) — the number that should be represented by the rules described above. It is guaranteed that n is a Fibonacci number.n is Fibonacci number =)because N is definitely a fibonacci number, and so is 0, so 0+0+n always works
I think it's obvious that problems 1D and 1E should've been in other order.
Sorry to interrupt, but can problem 1E use priority_queue?
I solved the Div1. B running DFS And i think there's a problem with my code and the algorithm is wrong but it was accepted by the test 21324539
That's a good luck Sometimes my algorithm was correct but I got wrong answer on test >= 100 U R so lucky
In Div2 C, I am using C++14 to solve the question. I have performed the same math as given in the editorial and to find the minimum value of x, I apply log. That is x >= n-log(LHS_value)_to_base_k. I am using double as the type for x and am finally storing (long long)(ceil(x)) as the answer and printing that. However, I am running into precision issues. For example, in one testcase, x came out to be 1 but ceil(x) got evaluated as 2. When I am submitting the same logic using Java, everything is working fine. Here are the 2 submissions:- C++ — 39201368 Java — 39201512
Long double will also work.