Could not find any related blog. Let's discuss here. Solution for D, E, J and L?
→ Pay attention
→ Top rated
| # | User | Rating |
|---|---|---|
| 1 | tourist | 3880 |
| 2 | jiangly | 3669 |
| 3 | ecnerwala | 3654 |
| 4 | Benq | 3627 |
| 5 | orzdevinwang | 3612 |
| 6 | Geothermal | 3569 |
| 6 | cnnfls_csy | 3569 |
| 8 | jqdai0815 | 3532 |
| 9 | Radewoosh | 3522 |
| 10 | gyh20 | 3447 |
→ Top contributors
| # | User | Contrib. |
|---|---|---|
| 1 | awoo | 161 |
| 1 | maomao90 | 161 |
| 3 | adamant | 156 |
| 4 | maroonrk | 153 |
| 5 | -is-this-fft- | 148 |
| 5 | atcoder_official | 148 |
| 5 | SecondThread | 148 |
| 8 | Petr | 147 |
| 9 | nor | 144 |
| 10 | TheScrasse | 142 |
→ Find user
→ Recent actions
Codeforces (c) Copyright 2010-2024 Mike Mirzayanov
The only programming contests Web 2.0 platform
Server time: Jul/27/2024 02:33:03 (i1).
Desktop version, switch to mobile version.
Supported by
User lists


| Name |
|---|











E: the following brute force works. Let's maintain the set of positions where the enemy king can be. Let's iterate over all our moves on depth 4, and look for the sequence of moves which leads to the smallest amount of available positions of the enemy king. Then make the first move out of the 4, and repeat the process. This leads to the win in 19 moves (starting from a1). To make it fast, one can first get to a1, and then output pre-calculated sequence of moves. ( Interesting question: is there a nice constructive solution ?)
J: it turns out that if x and x2 are "quaternary", then x consists only of 0's and 1's. We didn't prove this during the contest.
L: Petr and meshanya implemented some crazy 300-line segment tree there. I wonder if there is a simpler (implementation-wise) solution — other teams didn't seem to spend 1.5 hours on it.
D: no one solved it so it is hard to tell for sure, but at first glance, it seems that maintaining all the stuff in the rope/BST should do the trick. Though there are clearly lots of painful technical details, like merging lexems, etc.
In L we had an easy segment tree solution with a binary search. After fixing the minimal quality value of the rectangles, each of them bans a union of two rectangles to be the leftdown corner of the given shape. Then to find a non-banned point we use scanline with a segment tree returning the minimal value and its leftmost position and being able to add a value on the subsegment.
E: Kronecker found this solution: Suppose we start at c3. Then go c3-c4-c5-c6-c5-d4-d3. Not hard to prove that now the king can't be on first 4 verticals. Do it 2 more times (d3-d4-d5-d6-d5-e4-e3-e4-e5-e6-e5-f4-f3) and then f3-f4-f5-f6. Carefully go to c3 first, avoiding stalemate (WA 34).
J: First of all, fix the least significant digit of x to be 1. Now fix k least significant digits of x. We can restore (and check) k digits of x2. Now try all the possibilities for (k + 1)-th digit — no more then two of them will be good. It is like 220·20 on paper, but smaller in real life.
In J, one may notice that each digit of x is either 0 or 1. We noticed it just staring at the output, while other teams from our sector say that it can be proved with induction.
Me and Kaban-5 spent a lot of time trying to prove this but didn't succeed. If anyone has a proof I'm really interested in it though I'm pretty sure this is wrong.
J: it seems that if x is good, then every suffix of x is also good (ignoring leading zeros). Which gives an easy algorithm for generating good numbers quickly. During the contest I hallucinated that it must be true and got AC. I was surprised later when I realized it doesn't make much sense.
Can anyone prove/disprove it?
E: A simple BFS on (amazon position, mask of king's positions) works without any optimizations at all. A (somewhat speculative) reason for that is that there are rarely many options for the next move (for instance, jumping away too much will most likely result in being eaten), and also most of the move sequences are easy for the king to avoid and spread back across the board.
D: I'm not sure how to solve the problem if only curly brackets are allowed. I'm fairly sure this problem wouldn't be solved if it was the only problem in the set. yeputons, can you share some insight at how this can be done within reasonable time?
About problem D: unfortunately, there are no nice tricks which make the implementation significantly easier. I'm aware of two possible approaches (listed below). The main solution was implemented by Kurpilyansky, so you can address specific questions to him.
Approaches that I know:
do,for,identifier,{,+, etc. In order to do that efficiently, you have to be able to insert substrings into that treap: split treap, split corresponding lexem (if necessary), insert new lexems, possibly merging lexems on borders. Then you should come up with some monoid which tells you where to place new lines or spaces (see below).Now about the monoid: it definitely should store first/last lexem of a subprogram and some additional information for:
} elsesubstrings, which change the game. I'd process number of lines in conjunction with the next bullet which processes spaces (because newline depends on two neighboring tokens, very similar to spaces).for (int i = 0; i < n; i++)case correctly when we should not place a new line character. Here we should note that maximal "balance" of round brackets is four, so we can "precalculate" outcome for every "starting balance" and store it in treap's node.Technically, Kurpilyansky's solution has the following fields in a single treap node (except for what comes from treap itself): initial length of the segment (in source program), whether is has curly brackets, their balances (total and minimal prefix), balance of round brackets/number of lines for each starting balance of round brackets.
Where can I find the standings?
link
I'd like to note two things about the contest.
At the rules page at the official opencup site (link it is mentioned that the source limit is 64K. However, on Yandex.Contest it is 256K. After the end of the contest we learned that some team has asked a clarification about source limit and received this 256K constraint. I wonder why this clar wasn't made a public announcement and why the information on the official site differ.
In problem J, there was a phrase regarding quaternary numbers: "... a decimal integer without leading zeros..." For our team, it wasn't obvious if zero fulfills this requirement. Formally, a zero does have a leading zeros, putting aside that zero is the only digit of a number here. We asked a clarification on this and received a "no comments" answer. I think that mentioning zero explicitly would be a good taste here, like saying, for example, whether zero belongs to natural numbers for the sake of this exact problem.
And finally a tiny question to the authors: in I, was the simple backtracking solution (select the match for 1, recurse, select the match for 2, ...) with running full Kuhn matching for a pruning held in mind as an expected solution, or you have something that asymptotically fits the constraints better? This one got AC in 0.7 s with no optimizations (even without random shuffle).
For checking whether we need to go further in backtrack we searched for the increasing chain only once, so it's clear no more than O(ans·n3), but much faster in practice (94ms on system tests).
Our solution seems to be O(ans·n4) because we run O(n3) Kuhn O(ans·n) times (if I understand correctly, the backtracking has this bound because we make at most n spare descends for each valid answer, and it should be possible to build a test which matches the bound. This is 1011 which is far beyond the TL.
Searching for only one chain each time looks much more reasonable. I had this approach in mind while coding the solution, but the simple one appeared to be fast enough to stop further thinking. Anyway, happy that it can really be done that way.
I think that n4 may be replaced with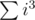 , because on i-th depth of recursion you have only n - i vertices to build matching, so complexity has
, because on i-th depth of recursion you have only n - i vertices to build matching, so complexity has 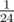 as the global constant, and it is just
as the global constant, and it is just 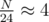 times slower.
times slower.
Why it is not O(ans·n2) DFSs?
OK, you are right, so the solution of ifsmirnov seems to be O(ans·n5). It would be interesting to hear authors' comments about these solutions, whether they tried to fail some of them and what was the largest number of operations they made them use.
It's possible to actually solve the problem in O(ans·n3). Instead of looking for increasing chain for each choice of the next edge in the matching one should run one dfs and find all increasing chains at once.
I've investigated a bit, and it turned out you are right.
As the author, I intended to accept most polynomial solutions and reject most exponential solutions. So I focused on this distinction, and didn't investigate polynomial solutions thoroughly. Please accept my apologies.
For the polynomial solutions involving construction of a perfect matching, they realistically can be as slow as O(knm2) where m is the number of edges: at each of the positions in the recursive search and each possible edge to add from a vertex (total km worst case), run O(nm) Kuhn matching algorithm. This can be optimized in a number of ways, like the ones already mentioned:
Maintain the current perfect matching and add at most one augmenting path each time (km × m).
Additionally, in every single depth-first search for an augmenting path, find augmenting paths through all possible first vertices instead of just one (kn × m).
My mistake was that I expected m to be small when there is at least one but at most 1000 perfect matchings, which is obviously false: it can be of order n2. If we discovered this in time, the constraints on n and k would be made smaller to make reasonable polynomial solutions pass, as they do now with weaker tests.
As for exponential solutions, there are solutions which do pass the tests.
If we consider vertices in the order of their current degree, we are quickly left with only vertices of degree at least 3. For such graphs, the conjecture is that the number of perfect matchings either is zero or grows exponentially with the number of vertices. I don't have a proof, but its plausibility is suggested by a similar result by Alexander Schrijver: for any k, a k-regular bipartite graph with 2n vertices has at least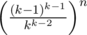 perfect matchings. So, the remaining part of the search happens on a very small graph, and is therefore fast as well.
perfect matchings. So, the remaining part of the search happens on a very small graph, and is therefore fast as well.
Note that sorting vertices by degree (even statically at start) speeds up polynomial solutions as well, for the same reasons.
Anyway, I added the tests suggested by Kaban-5 and ifsmirnov to Yandex.Contest. It turned out that, out of 51 solutions accepted up to now, only 19 still pass all tests. This of course won't change the official results, the tests are added only for upsolving purposes.
It seems that nobody has posted an asymptotically satisfying solution for problem I. In the contest we had O(k·n2 + n3) solution:
First, find any perfect matching. Then use the following function recursively to generate all matchings:
Given a graph, one perfect matching in it and a set of fixed vertices, generate all matchings in that graph where the fixed vertices are matched to the given vertices in the matching. The function is implemented as follows:
While there is a vertex with degree one that is not fixed, fix that vertex and the vertex where it is matched and remove all other edges incident to them.
If all vertices are fixed, add the matching to the list of matchings and return. Otherwise it is easy to find an augmenting cycle in the graph, which changes the matching. Let u be the first vertex in the augmenting cycle and v to be the vertex where u is matched originally. We recurse to two cases, the cases where v is matched to u and the cases where v is not matched to u. To recurse to the first case, just fix v and u, delete all other edges incident to v and u, and give the same perfect matching to the function. To recurse to the second case, remove edge between v and u and give the matching obtained by augmenting by the cycle to the function.
Time complexity of a single function call is O(n2) and there are O(k) function calls because the calls form a search tree where each leaf is a solution and each inner node has degree 2. I'm not sure if this algorithm could be optimized to O(n·k) by using some efficient graph data structures since all operations of the first part are quite simple and the second part can be implemented in O(n) if the graph is given in an adjacency list.
This runs in 31ms in the current tests.
Nice! The naive recursive solution visits km states in the worst case: it quickly splits initially into k paths of length of order n and then follows them. What you have is a neat trick to reduce it to just O(k) states.
The solution with lazy matching reconstruction and initial ordering passes the current test set in 55ms. The complexity without ordering is O(km × m), but ordering reduces one of these factors of m down to something less than n and more like a constant, and everything less than kmn is enough already.
exist any chance that the contest be added to the gym?
What about B and K?
B: We have to represent 6·k as sum of centered hexagonal numbers with minimal number of summands. it's not hard to prove that these numbers can be calculated as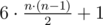 (you can just read wikipedia article). So number of summands will always be a multiple of 6. And it's possible to find exaclty 6 such numbers with sum 6·k.
(you can just read wikipedia article). So number of summands will always be a multiple of 6. And it's possible to find exaclty 6 such numbers with sum 6·k.
Our solution may be not the easiest one, but we have a proof of it's correctness :)
We have to represent a = k - 1 as sum of at most 6 triangular numbers (which are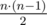 in the formula above). In fact there is a theorem allowing to represent any integer nonnegative number as sum of at most 3 such numbers, and we can use 6. As a ≤ 1018, we can make at most 3 'greedy' steps, subtracting from a the largest triangular number less or equal to a, and reduce the problem to
in the formula above). In fact there is a theorem allowing to represent any integer nonnegative number as sum of at most 3 such numbers, and we can use 6. As a ≤ 1018, we can make at most 3 'greedy' steps, subtracting from a the largest triangular number less or equal to a, and reduce the problem to 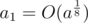 . Finally we can precalculate optimal answer for small values using dynamic programming (we calculated up to 104), it will not contain more than 3 triangular numbers. So total number of summands will not exceed 6.
. Finally we can precalculate optimal answer for small values using dynamic programming (we calculated up to 104), it will not contain more than 3 triangular numbers. So total number of summands will not exceed 6.
Turned out to be pretty easy and pleasant to code: http://pastebin.com/hywvVmAm
Thanks!
Yeah, that is the originally intended solution: meet-in-the-middle for greedy from the top and dynamic programming from the bottom.
However, as we can use up to 6 numbers and it is always possible to use only 3, the number of possibilities is very large. So other solutions are also accepted. For example, backtracking in greedy order finishes momentarily. A randomized search with distribution skewed enough to the top is also accepted.
The interesting fact about this problem is that the greedy solution (always take the greatest possible triangular number) does not work, but the smallest counterexample is the number 359 026 206. Here is how n - 1 is greedily split into triangular numbers: