Two months ago, I came across a problem.
Initially there are n elements, they are in n tiles.
There are 3 kinds of queries:
- merge two tiles into one tile.
- split one tile into two tiles. (Formally for a tile of size k, split it into two tiles of size k1 and k2, k=k1+k2, the first tile contains the smallest k1 elements and the second tile contains the rest)
- find the k-th smallest element in one tile.
Recently I found this technique http://blog.csdn.net/zawedx/article/details/51818475 (in Chinese) which can be used to solve this problem. This blog is my own explanation :p
First, let's suppose the values in the sorted lists are integers between 1~n. If not, you may just sort and map them.
Let's build a segment tree for every sorted list, segment trees are built based on values (1~n). In every node of a segment tree stores how many numbers are in this range, let's call this the value of a node.
It seems that it requires O(nlogn) space to store every segment tree, but we can simply ignore the nodes that value=0, and really allocate these nodes only when their value become >0.
So for a sorted list with only one element, we simply build a chain of this value, so only O(logn) memory is needed.
int s[SZ]/*value of a node*/,ch[SZ][2]/*a node's two children*/;
//make a seg with only node p, return in the first argument
//call with sth. like build(root,1,n,value);
void build(int& x,int l,int r,int p)
{
x=/*a new node*/; s[x]=1;
if(l==r) return;
int m=(l+r)>>1;
if(p<=m) build(ch[x][0],l,m,p);
else build(ch[x][1],m+1,r,p);
}
When we split a segment tree (sorted list), simply split two children recursively:
//make a new node t2, split t1 to t1 and t2 so that s[t1]=k
void split(int t1,int& t2,int k)
{
t2=/*a new node*/;
int ls=s[ch[t1][0]]; //size of t1's left child
if(k>ls) split(ch[t1][1],ch[t2][1],k-ls); //split the right child of t1
else swap(ch[t1][1],ch[t2][1]); //all right child belong to t2
if(k<ls) split(ch[t1][0],ch[t2][0],k); //split the left child of t1
s[t2]=s[t1]-k; s[t1]=k;
}
When we merge two sorted lists, merge them forcely:
//merge trees t1&t2, return merged segment tree (t1 in fact)
int merge(int t1,int t2)
{
if(t1&&t2);else return t1^t2; //nothing to merge
ch[t1][0]=merge(ch[t1][0],ch[t2][0]);
ch[t1][1]=merge(ch[t1][1],ch[t2][1]);
s[t1]+=s[t2]; /*erase t2, it's useless now*/ return t1;
}
Also, just query k-th simply.
//query k-th of segment tree x[l,r]
int ask(int x,int l,int r,int k)
{
if(l==r) return l;
int ls=s[ch[x][0]]; //how many nodes in left child
int m=(l+r)>>1;
if(k>ls) return ask(ch[x][1],m+1,r,k-ls);
return ask(ch[x][0],l,m,k);
}
It looks very simple, isn't it? But its total complexity is in fact O(nlogn).
Happy new year~











can we use this skill to solve problem like this
It seems kinda unrelated, so I guess it won't be easy
Yes, you can use it to solve this problem in O(nlogn).
(notice: I use 'substring' to represent continuous subsequence of the sequence)
The main idea is to represent the current sequence with a set of sorted substrings (using
std::setetc). For each sorted substring, store this kind of segment tree and the order (increasing or decreasing). Initially, you can represent the original sequence with just n sorted substrings of length 1.When you need to sort a range, find the relevant range in set. Notice that the two points of the range might not be the border of some sorted substrings in the set, in this case you can split the substrings contain these points into two halves so that the points of the query become borders of two sorted substrings.
After sorting, these sorted substrings should merge into one sorted substring. Just merge them forcely and maintain in the set.
The complexity is obviously O(nlogn). Also it can support online queries (e.g. what is the k-th number of the sequence currently.)
Code please?
http://paste.ubuntu.com/25851896/
Thanks for the nice tip! I think this problem may be related?
Yes, I think it can be used to solve this problem also.
I was trying to solve this problem using the above method but getting MLE :( n = 1e6 in the problem and memory limit is 128 MB.
Oh the memory limit does seem too tight. You can try merging splay trees (from small to large), by finger theorem it's also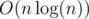 .
.
If you will solve this task via dfs, which visit the largest subtree first, the memory complexity will be O(N) and such a solution gets OK actually. If I'm not wrong, we can prove that at one point in time we will not need more than 4N segment tree nodes, and that fits in ML.
Wow!! Thanks a lot MrDindows. Got AC with the change. I get the intuition that solving for the larger sub-tree first will require lesser nodes. But how is it reducing the memory complexity from O(nlogn) to O(n)? Can you give a short proof or a hint towards it?
With such dfs order at any moment we can have not more than not-merged trees, because the size of each next tree should be at least twice smaller than previous. Let's assume n = 220, then in worst case we will have the trees of sizes: 20, 21, 22, ..., 219. (Worst case is when we have maximum number of trees, because the more trees — the more nodes). The maximum node count in the tree with 2k numbers is (2k + 1 - 1) + 2k·(20 - k), and the sum of these values is equal to 4·220 - 44.
not-merged trees, because the size of each next tree should be at least twice smaller than previous. Let's assume n = 220, then in worst case we will have the trees of sizes: 20, 21, 22, ..., 219. (Worst case is when we have maximum number of trees, because the more trees — the more nodes). The maximum node count in the tree with 2k numbers is (2k + 1 - 1) + 2k·(20 - k), and the sum of these values is equal to 4·220 - 44.
So the worst test case is the almost full binary tree, where leafi = reverseBits(i).
Got it, thanks.
I don't understand merge function at all.
Aren't t1 and t2 just the id_numbers of some nodes? Then what does t1^t2 even means? If it's not a c++ code you wrote then how to do this XOR operation in O(1)?
It's implicit segment tree, you create the node when you need it. That's why t1 or t2 can be zero, so t1^t2 will return max(t1, t2);
You mean that line can just be written like this? :
if(t1==0 || t2==0)return max(t1,t2);
Then aren't we going into all nodes of these two segment trees? Isn't the complexity of calling merge function O(T1.size()+T2.size())?
If I'm wrong about that line so what does t1&&t2 means?
Yes,
if(t1==0 || t2==0)return max(t1,t2);No, it's like O(min(T1.size(), T2.size())). We are going only into common vertices, that should be merged.
t1&&t2is equal to(t1 != 0) && (t2 != 0)Correct me if I’m wrong, but I believe using the same argument you should achieve the same amortized complexity using treaps, right? The main point here is the memory overhead of seg trees, which might hinder performance in some cases.
memory overhead of seg trees, which might hinder performance in some cases.
Well the structure of treap is dynamic, so I don't actually know how to merge them..
Source: Wikipedia
I will test and compare both data structures today and I’ll get back with some results.
Interestingly enough, I found treaps to be a tad bit slower than segtrees on random input. Nonetheless, they don't seem to break complexity. Feel free to look at the code and experiment though, if you notice any mistakes on the treap part or if you think treaps would fil on certain (non-random) test data.
Results: https://pastebin.com/4ivKeAZR
Source code: https://pastebin.com/ua02DbPY
Does this merging technique work only for segtrees storing set structures? Like, when sum(x, x) is at most 1?