Hello Codeforces,
It has been a long while, but in this project we close the long-standing open problem proposed by Umnik 2021. You can try it here (deployed on my tiny server, be nice!) while supplies last. Currently I only imported problems from Codeforces & BZOJ (the dead Chinese OJ) but adding other OJs should be easy as long as we have the statements crawled (PRs?).
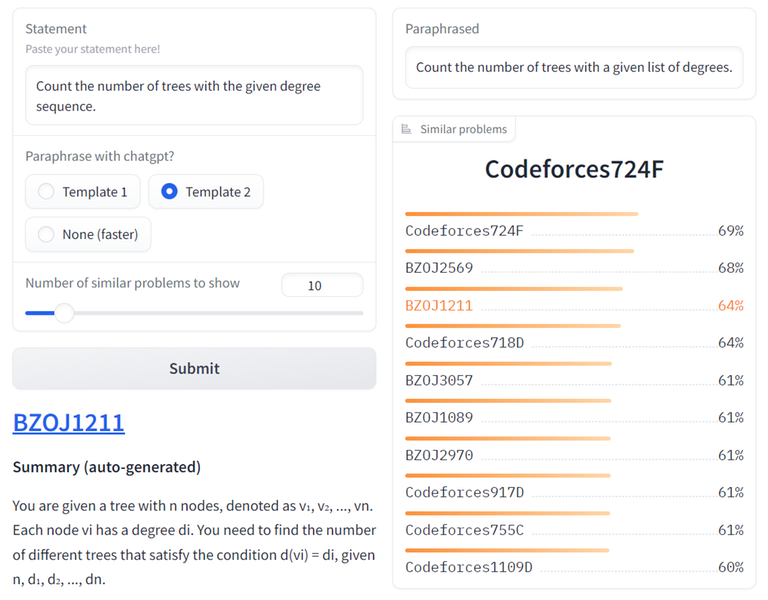
Cheers!









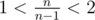 ,
, 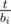 kinds of hats with
kinds of hats with 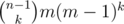 .
.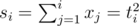 ,
,  , we can precalculate all possible
, we can precalculate all possible 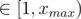 , then for every
, then for every 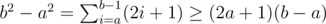 , then
, then  , its complexity is
, its complexity is 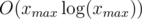 .
.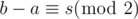 .
.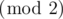 ,
,  , it's easy to arrive at such arrangements.
, it's easy to arrive at such arrangements.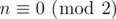 , try to query
, try to query  , try to query
, try to query 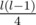 (for a segment of length
(for a segment of length 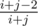 , and if the maximum is chosen, there are
, and if the maximum is chosen, there are 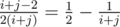 .
.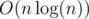 solution.
solution.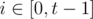 ).
).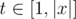 )
)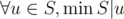 .
.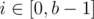 ),
), 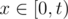 ,
, 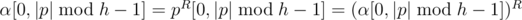 , then
, then 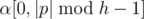 is palindromic. Similarly
is palindromic. Similarly 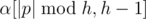 is also palindromic. When
is also palindromic. When  , so
, so  , at least one of
, at least one of 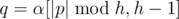 , so
, so 
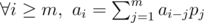 . (Obviously, if
. (Obviously, if 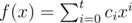 , we define
, we define 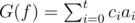 .
.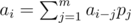 , if we let
, if we let 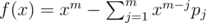 , then
, then 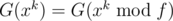 .
.
