Idea: sunset Developer: sunset
1 sounds like the minimum value we can get. Why? Is it always true?
When n ≤ 2, we can do nothing.
When n ≥ 3, since 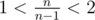 , n - 1 isn't a divisor of n, so we can choose it and get 1 as the result.
, n - 1 isn't a divisor of n, so we can choose it and get 1 as the result.
#include <bits/stdc++.h>
using namespace std;
int main() {
int n;
scanf("%d", &n);
if (n == 2) {
puts("2");
} else {
puts("1");
}
return 0;
}
Idea: yanQval Developer: yanQval
Consider the number of people wearing hats of the same color.
let bi = n - ai represent the number of people wearing the same type of hat of i-th person.
Notice that the person wearing the same type of hat must have the same bs. Suppose the number of people having the same bi be t, there would be exactly 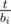 kinds of hats with bi wearers. Therefore, t must be a multiple of bi. Also this is also sufficient, just give bi people a new hat color, one bunch at a time.
kinds of hats with bi wearers. Therefore, t must be a multiple of bi. Also this is also sufficient, just give bi people a new hat color, one bunch at a time.
#include <bits/stdc++.h>
using namespace std;
const int maxn = 100010;
int n;
pair<int,int> a[maxn];
int Ans[maxn],cnt;
int main(){
ios::sync_with_stdio(false);
cin>>n;
for(int i=1;i<=n;i++){
cin>>a[i].first;
a[i].first=n-a[i].first;
a[i].second=i;
}
sort(a+1,a+n+1);
for(int l=1,r=0;l<=n;l=r+1){
for(r=l;r<n&&a[r+1].first==a[r].first;++r);
if((r-l+1)%a[l].first){
cout<<"Impossible"<<endl;
return 0;
}
for(int i=l;i<=r;i+=a[l].first){
cnt++;
for(int j=i;j<i+a[l].first;++j)Ans[a[j].second]=cnt;
}
}
cout<<"Possible"<<endl;
for(int i=1;i<=n;i++)cout<<Ans[i]<<' ';
return 0;
}
No hint here :)
Let f[i][j] be the ways that there're j bricks of a different color from its left-adjacent brick among bricks numbered 1 to i. Considering whether the i-th brick is of the same color of i - 1-th, we have f[i][j] = f[i - 1][j] + f[i - 1][j - 1](m - 1). f[1][0] = m and the answer is f[n][k].
Also, there is a possibly easier solution. We can first choose the bricks of a different color from its left and then choose a different color to color them, so the answer can be found to be simply 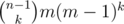 .
.
//quadratic
#include <bits/stdc++.h>
using namespace std;
const int MOD=998244353;
int n,m,k;
long long f[2005][2005];
int main()
{
scanf("%d%d%d",&n,&m,&k);
f[1][0]=m;
for(int i=1;i<n;++i)
for(int j=0;j<=k;++j)
(f[i+1][j]+=f[i][j])%=MOD,
(f[i+1][j+1]+=f[i][j]*(m-1))%=MOD;
printf("%d\n",int(f[n][k]));
}
//linear
#include <bits/stdc++.h>
using namespace std;
const int MOD=998244353;
typedef long long ll;
ll fac[2333],rfac[2333];
ll qp(ll a,ll b)
{
ll x=1; a%=MOD;
while(b)
{
if(b&1) x=x*a%MOD;
a=a*a%MOD; b>>=1;
}
return x;
}
int n,m,k;
int main()
{
scanf("%d%d%d",&n,&m,&k);
fac[0]=1;
for(int i=1;i<=n;++i)
fac[i]=fac[i-1]*i%MOD;
rfac[n]=qp(fac[n],MOD-2);
for(int i=n;i;--i)
rfac[i-1]=rfac[i]*i%MOD;
printf("%lld\n",m*qp(m-1,k)%MOD*fac[n-1]%MOD
*rfac[k]%MOD*rfac[n-1-k]%MOD);
}
Idea: fateice Developer: fateice
Sorry for the weak pretest.
Consider the MST of the graph.
Consider the minimum spanning tree formed from the n vertexes, we can find that the distance between two vertexes is the maximum weight of edges in the path between them in the minimum spanning tree (it's clear because of the correctness of Kruskal algorithm).
Take any minimum spanning tree and consider some edge in this spanning tree. If this edge has all special vertexes on its one side, it cannot be the answer. Otherwise, it can always contribute to the answer, since for every special vertex, we can take another special vertex on the other side of this edge. Therefore, answers for all special vertexes are the maximum weight of the edges that have special vertexes on both sides.
Besides implementing this directly, one can also run the Kruskal algorithm and maintain the number of special vertexes of each connected component in the union-find-set. Stop adding new edges when all special vertexes are connected together and the last edge added should be the answer.
#include<bits/stdc++.h>
#define L long long
#define vi vector<int>
#define pb push_back
using namespace std;
int n,m,t,f[100010],p;
bool a[100010];
inline int fa(int i)
{
return f[i]==i?i:f[i]=fa(f[i]);
}
struct edge
{
int u,v,w;
inline void unit()
{
u=fa(u);
v=fa(v);
if(u!=v)
{
if(a[u])
f[v]=u;
else
f[u]=v;
if(a[u] && a[v])
p--;
if(p==1)
{
for(int i=1;i<=t;i++)
printf("%d ",w);
printf("\n");
exit(0);
}
}
}
}x[100010];
inline bool cmp(edge a,edge b)
{
return a.w<b.w;
}
int main()
{
int i,j;
scanf("%d%d%d",&n,&m,&t);
p=t;
for(i=1;i<=t;i++)
{
scanf("%d",&j);
a[j]=1;
}
for(i=1;i<=m;i++)
scanf("%d%d%d",&x[i].u,&x[i].v,&x[i].w);
sort(x+1,x+m+1,cmp);
for(i=1;i<=n;i++)
f[i]=i;
for(i=1;i<=m;i++)
x[i].unit();
return 0;
}
How to solve n = 2?
Let 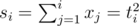 , xmax = 2 × 105.
, xmax = 2 × 105.
Since x2i = s2i - s2i - 1 = t2i2 - t2i - 12 ≥ (t2i - 1 + 1)2 - t2i - 12 = 2t2i - 1 + 1, so 2t2i - 1 + 1 ≤ xmax, t2i - 1 < xmax.
For every  , we can precalculate all possible (a, b)s so that x = b2 - a2: enumerate all possible a
, we can precalculate all possible (a, b)s so that x = b2 - a2: enumerate all possible a 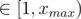 , then for every a enumerate b from small to large starting from a + 1 and stop when b2 - a2 > xmax, record this (a, b) for x = b2 - a2. Since
, then for every a enumerate b from small to large starting from a + 1 and stop when b2 - a2 > xmax, record this (a, b) for x = b2 - a2. Since 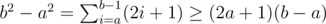 , then
, then  , its complexity is
, its complexity is 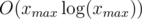 .
.
Now, we can try to find a possible s from left to right. Since x2i - 1 is positive, we need to ensure t2i - 2 < t2i - 1. Becuase x2i = t2i2 - t2i - 12, we can try all precalculated (a, b)s such that x2i = b2 - a2. If we have several choices, we should choose the one that a is minimum possible, because if the current sum is bigger, it will be harder for the remaining number to keep positive.
Bonus: Solve n ≤ 103, x2i ≤ 109.
t2i2 - t2i - 12 = (t2i - t2i - 1)(t2i + t2i + 1). Factor x2i.
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef pair<int,int> pii;
int n;
ll sq[100099];
#define S 200000
vector<pii> v[S+55];
int main()
{
for(int i=1;i<=S;++i)
{
if(i*2+1>S) break;
for(int j=i+1;j*(ll)j-i*(ll)i<=S;++j)
v[j*(ll)j-i*(ll)i].push_back(pii(i,j));
}
scanf("%d",&n);
for(int i=2;i<=n;i+=2)
{
int x; scanf("%d",&x);
for(auto t:v[x])
if(sq[i-2]<t.first)
{
sq[i-1]=t.first,sq[i]=t.second;
break;
}
if(!sq[i-1])
{puts("No"); return 0;}
}
puts("Yes");
for(int i=1;i<=n;++i)
printf("%lld%c",sq[i]*(ll)sq[i]-sq[i-1]
*(ll)sq[i-1]," \n"[i==n]);
}
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
int n;
vector<int> d[200099];
ll su[100099],x[100099];
int main()
{
for(int i=1;i<=200000;++i)
for(int j=i;j<=200000;j+=i)
d[j].push_back(i);
scanf("%d",&n);
for(int i=2;i<=n;i+=2)
scanf("%lld",x+i);
for(int i=2;i<=n;i+=2)
{
for(auto j:d[x[i]])
{
int a=j,b=x[i]/j;
if(((a+b)&1)||a>=b) continue;
int s1=(b-a)/2;
if(su[i-2]<(ll)s1*s1)
x[i-1]=(ll)s1*s1-su[i-2];
}
if(x[i-1]==0)
{
puts("No");
return 0;
}
su[i-1]=su[i-2]+x[i-1];
su[i]=su[i-1]+x[i];
}
puts("Yes");
for(int i=1;i<=n;i++)
printf("%lld%c",x[i]," \n"[i==n]);
}
Idea: TLE Developer: fateice, TLE
Yet another binary search?
What about parity?
Assuming the number of 1s changed from a to b after flipping a range of length s.
Let the number of 1s in the range before this flip be be t, then b - a = (l - t) - t = s - 2t, so 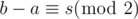 .
.
So if we made a query l, r, the parities of the lengths of [1, r] and [l, n] are different, we can find out which one is actually flipped by parity of delta. Also if we only want [1, r] or [l, n] to be flipped and nothing else, we can keep querying l, r and record all the flips happened until it's the actual case (since flipping a range twice is equivalent to no flipping at all). The expected number of queries needed is 3.
Let sa, b be, currently a ≡ the number of times [1, r] is flipped 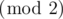 , b ≡ the number of times [r, n] is flipped
, b ≡ the number of times [r, n] is flipped 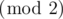 , the expectation of remaining number of queries needed to complete our goal. Then s1, 0 = 0 (goal), we're going to find out s0, 0.
, the expectation of remaining number of queries needed to complete our goal. Then s1, 0 = 0 (goal), we're going to find out s0, 0.
s0, 0 = (s0, 1 + s1, 0) / 2 + 1, s0, 1 = (s0, 0 + s1, 1) / 2 + 1, s1, 1 = (s1, 0 + s0, 1) / 2 + 1.
Solve this equation you'll get s0, 0 = 3, s0, 1 = 4, s1, 1 = 3.
Since  , it's easy to arrive at such arrangements.
, it's easy to arrive at such arrangements.
When 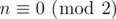 , try to query (1, 1), (1, 1), (2, 2), (2, 2), (3, 3), (3, 3)...(n, n), (n, n) and use the method described above to flip [1, 1], [1, 1], [1, 2], [1, 2], [1, 3], [1, 3]...[1, n], [1, n]. Thus we'll know s1, s1 + s2, s1 + s2 + s3...s1 + s2 + ... + sn and s becomes obvious.
, try to query (1, 1), (1, 1), (2, 2), (2, 2), (3, 3), (3, 3)...(n, n), (n, n) and use the method described above to flip [1, 1], [1, 1], [1, 2], [1, 2], [1, 3], [1, 3]...[1, n], [1, n]. Thus we'll know s1, s1 + s2, s1 + s2 + s3...s1 + s2 + ... + sn and s becomes obvious.
When  , try to query (2, n), (2, n), (1, 2), (1, 2), (2, 3), (2, 3)...(n - 1, n), (n - 1, n) and use the method described above to flip [2, n], [2, n], [1, 2], [1, 2][1, 3], [1, 3]...[1, n], [1, n]. Thus we'll know s2 + s3 + ... + sn, s1 + s2, s1 + s2 + s3...s1 + s2 + ... + sn and s also becomes obvious.
, try to query (2, n), (2, n), (1, 2), (1, 2), (2, 3), (2, 3)...(n - 1, n), (n - 1, n) and use the method described above to flip [2, n], [2, n], [1, 2], [1, 2][1, 3], [1, 3]...[1, n], [1, n]. Thus we'll know s2 + s3 + ... + sn, s1 + s2, s1 + s2 + s3...s1 + s2 + ... + sn and s also becomes obvious.
Also, we can flip every range only once instead of twice by recording whether every element is currently flipped or not, although it will be a bit harder to write.
#include <bits/stdc++.h>
using namespace std;
int n,ss[10005],sn=0,q[333];
bool tf(int l,int r)
{
cout<<"? "<<l<<" "<<r<<endl<<flush;
cin>>ss[++sn];
return (ss[sn]-ss[sn-1])&1;
}
int main()
{
cin>>n>>ss[0]; q[n]=ss[0];
for(int i=1;i<n;++i)
{
int j=i-n%2;
if(j==0)
{
int t[2]={0,0},u=ss[sn];
while(t[0]!=1||t[1]!=0)
t[tf(2,n)]^=1;
int v=ss[sn];
q[i]=q[n]-(n-1-v+u)/2;
while(t[0]||t[1])
t[tf(2,n)]^=1;
}
else
{
int t[2]={0,0},u=ss[sn];
while(t[0]!=1||t[1]!=0)
t[(tf(j,i)^i)&1]^=1;
int v=ss[sn];
q[i]=(i-v+u)/2;
while(t[0]||t[1])
t[(tf(j,i)^i)&1]^=1;
}
}
cout<<"! ";
for(int i=1;i<=n;++i)
printf("%d",q[i]-q[i-1]);
cout<<endl<<flush;
}
1081G - Mergesort Strikes Back
Idea: quailty Developer: fateice, TLE, sunset
How does "merge" work? What is this "mergesort" actually doing?
First, consider how "merge" will work when dealing with two arbitrary arrays. Partition every array into several blocks: find all elements that are larger than all elements before them and use these elements as the start of the blocks. Then, by 'merging' we're just sorting these blocks by their starting elements. (This is because that when we decided to put the start element of a block into the result array, the remaining elements in the block will be sequentially added too since they're smaller than the start element)
Now back to the merge sort. What this "mergesort" doing is basically dividing the array into several segments (i.e. the ranges reaching the depth threshold). In every segment, the relative order stays the same when merging, so the expected number of inversions they contribute is just 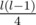 (for a segment of length l). Again suppose every segment is divided into blocks aforementioned, we're just sorting those blocks altogether by the beginning elements.
(for a segment of length l). Again suppose every segment is divided into blocks aforementioned, we're just sorting those blocks altogether by the beginning elements.
Let's consider inversions formed from two blocks in two different segments. Say the elements forming the inversion are initially the i-th and j-th of those two segments (from left to right), then the blocks they belong start from the maximum of the first i-th and the first j-th of those two segments. Consider the maximum among these i + j numbers, if it is one of these two elements, the inversion can't be formed. The probability that the maximum is neither i nor j is 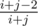 , and if the maximum is chosen, there are 50% percent of odds that the order of i and j is different from that of two maximums, because these two elements' order can be changed by swapping these two elements while leaving the maximums' order unchanged. So their probability of forming an inversion is just
, and if the maximum is chosen, there are 50% percent of odds that the order of i and j is different from that of two maximums, because these two elements' order can be changed by swapping these two elements while leaving the maximums' order unchanged. So their probability of forming an inversion is just 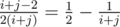 .
.
Enumerate two blocks and i and precalculate the partial sum of reciprocals, we can calculate the expectation of inversions formed from these two blocks in O(n) time. However, there might be O(n) blocks. But there is one more property for this problem: those segments are of at most two different lengths. By considering same length pairs only once, we can get a O(n) or 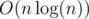 solution.
solution.
Do an induction on k.
Suppose for k - 1 we have only segments of length a and a + 1.
If 2|a, let a = 2t, from 2t and 2t + 1 only segments of length t and t + 1 will be formed.
Otherwise, let a = 2t + 1, from 2t + 1 and 2t + 2 still only segments of length t and t + 1 will be formed.
Bonus: solve this problem when the segments' length can be arbitary and n ≤ 105.
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
#define fi first
#define se second
#define SZ 123456
int n,k,MOD,ts[SZ],tn=0;
ll inv[SZ],invs[SZ];
ll qp(ll a,ll b)
{
ll x=1; a%=MOD;
while(b)
{
if(b&1) x=x*a%MOD;
a=a*a%MOD; b>>=1;
}
return x;
}
void go(int l,int r,int h)
{
if(h<=1||l==r) ts[++tn]=r-l+1;
else
{
int m=(l+r)>>1;
go(l,m,h-1); go(m+1,r,h-1);
}
}
map<ll,int> cnt;
ll calc(int a,int b)
{
ll ans=a*(ll)b%MOD;
for(int i=1;i<=a;++i)
ans-=(invs[i+b]-invs[i])*2LL,ans%=MOD;
return ans;
}
int main()
{
scanf("%d%d%d",&n,&k,&MOD);
for(int i=1;i<=max(n,2);++i)
inv[i]=qp(i,MOD-2),
invs[i]=(invs[i-1]+inv[i])%MOD;
go(1,n,k); ll ans=0;
for(int i=1;i<=tn;++i)
++cnt[ts[i]],ans+=ts[i]*(ll)(ts[i]-1)/2,ans%=MOD;
for(auto t:cnt)
if(t.se>=2)
ans+=calc(t.fi,t.fi)*((ll)t.se*(t.se-1)/2%MOD),ans%=MOD;
for(auto a:cnt)
for(auto b:cnt)
if(a.fi<b.fi)
ans+=calc(a.fi,b.fi)*((ll)a.se*b.se%MOD),ans%=MOD;
ans=ans%MOD*inv[2]%MOD;
ans=(ans%MOD+MOD)%MOD;
printf("%d\n",int(ans));
}
Idea: TLE Developer: TLE, sunset
This problem is quite educational and we didn't expect anyone to pass. :P
What will be counted twice?
Warning: This editorial is probably new and arcane for ones who are not familiar with this field. If you just want to get a quick idea about the solution, you can skip all the proofs (they're wrapped in spoiler tags).
Some symbols: All indices of strings start from zero. xR stands for the reverse of string x. (e.g. 'abc'R = 'cba'), xy stands for concatenation of x and y. (e.g. x = 'a', y = 'b', xy = 'ab'), xa stands for concatenation of a copies of x (e.g. x = 'ab', x2 = 'abab'). x[a, b] stands for the substring of x starting and ending from the a-th and b-th character. (e.g. 'abc'[1, 2] = 'bc')
Border of x: strings with are common prefix & suffix of x. Formally, x has a border of length t (x[0, t - 1]) iff xi = x|x| - t + i (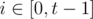 ).
).
Period of x: x has a period of length t iff xi = xi + t (0 ≤ i < |x| - t). When t||x| we also call t a full period. From the formulas it's easy to see x has a period of length t iff x has a border of length |x| - t. (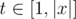 )
)
Power: x is a power iff the minimum full period of x isn't |x|. e.g. abab is a power.
Lemma 1 (weak periodicity lemma): if p and q are periods of s, p + q ≤ |s|, gcd(p, q) is also a period of s.
Suppose p < q, d = q - p.
If |s| - q ≤ i < |s| - d, si = si - p = si + d.
If 0 ≤ i < |s| - q, si = si + q = si + q - p = si + d.
So q - p is also a period. Using Euclid algorithm we can get gcd(p, q) is a period.
Lemma 2: Let S be the set of period lengths ≤ |s| / 2 of s, if S is non-empty, 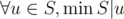 .
.
Let min S = v, since v + u ≤ |s|, gcd(v, u) is also a valid period, so gcd(v, u) ≥ v, v|u.
Let border(x) be the longest (not-self) border of x. e.g. border('aba') = 'a', border('ab') = ".
If x is a palindrome, its palindromic prefix and suffix must be its border. Therefore, its (not-self) longest palindromic prefix (suffix) is border(x).
Let |x| = a, x has a border of length b iff xi = xa - b + i (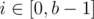 ), x has a palindromic prefix of length b iff xi = xb - 1 - i (
), x has a palindromic prefix of length b iff xi = xb - 1 - i (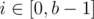 ). Since xi = xa - 1 - i, they are just the same.
). Since xi = xa - 1 - i, they are just the same.
If S = pq, p and q are palindromic and non-empty, we call (p, q) a palindromic decomposition of S. If S = pq, p and q are palindromic, q is non-empty (p can be empty) we call (p, q) a non-strict palindromic decomposition of S.
Lemma 3: if S = x1 x2 = y1 y2 = z1 z2, |x1| < |y1| < |z1|, x2, y1, y2, z1 are palindromic and non-empty, then x1 and z2 are also palindromic.
Let z1 = y1 v.
vR is a suffix of y2, also a suffix of x2. So v is a prefix of x2, then x1v is a prefix of z1.
Since y1 is a palindromic prefix of z1, z1 = y1 v, |v| is a period of z1. Since x1v is a prefix, so |v| is also a period of x1 v.
Suppose t be some arbitary large number (you can think of it as ∞), then x1 is a suffix of vt.
Since vR is prefix of z1, x1 is a prefix of (vR)t. So x1R is a suffix of vt, then x1 = x1R, so x1 is palindromic. z2 is palindromic similarly.
Lemma 4: Suppose S has some palindromic decomposition. Let the longest palindromic prefix of S be a, S = ax, longest palindromic suffix of S be b, S = yb. At least one of x and y is palindromic.
If none of them are palindromic, let S = pq be a valid palindromic decomposition of S, then S = yb = pq = ax, by Lemma 3, contradiction.
Lemma 5: S = p1 q1 = p2 q2 (|p1| < |p2|, p1, q1, p2, q2 are palindromic, q1 and q2 are non-empty), then S is a power.
We prove this by proving gcd(|p2| - |p1|, |S|) is a period.
Let |S| = n, |p2| - |p1| = t.
Because p1 is a palindromic prefix of p2, t is a period of p2. Similarly t is a period of q1. Since they have a common part of length t (namely S[p1, p2 - 1]), t is a period of S. So t is a period of S.
For 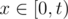 , sx = s|p2| - 1 - x = sn - 1 + |p1| - (|p2| - 1 - x) = sn - t + x (first two equations are because p2 and q1 and palindromic). So n - t is also a period of S.
, sx = s|p2| - 1 - x = sn - 1 + |p1| - (|p2| - 1 - x) = sn - t + x (first two equations are because p2 and q1 and palindromic). So n - t is also a period of S.
Since t + n - t = n, gcd(t, n - t) = gcd(t, n) is also a period of S. (weak periodicity lemma)
Lemma 6: Let S = p1 q1 = p2 q2 = ... = pt qt be all non-strict palindromic decompositions of S, h be the minimum full period of S. When t ≠ 0, t = |S| / h.
From Lemma 5, it's clear that h = |S| iff t = 1. In the following t ≥ 2 is assumed.
Let α = S[0, h - 1], because α is not a power (otherwise s will have smaller full period), α has at most one non-strict palindromic decomposition (from Lemma 5).
Let S = pq be any non-strict palindromic decomposition, then max(|p|, |q|) ≥ h. When |p| ≥ h, α = p[0, h - 1], so 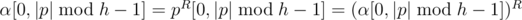 , then
, then 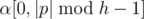 is palindromic. Similarly
is palindromic. Similarly 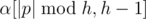 is also palindromic. When |q| ≥ h similar arguments can be applied. Therefore,
is also palindromic. When |q| ≥ h similar arguments can be applied. Therefore, 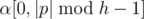 and
and 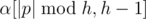 is a non-strict palindromic decomposition of α.
is a non-strict palindromic decomposition of α.
Therefore, α has a non-strict palindromic decomposition. Let its only non-strict palindromic decomposition be α[0, g - 1] and α[g, h - 1]. Therefore, every pi must satisfy  , so t ≤ |s| / h. Also, these all |s| / h decompositions can be obtained.
, so t ≤ |s| / h. Also, these all |s| / h decompositions can be obtained.
Lemma 7: Let S = p1 q1 = p2 q2 = ... = pt qt be all non-strict palindromic decompositions of S. (|pi| < |pi + 1|) For every  , at least one of pi = border(pi + 1) and qi + 1 = border(qi) is true.
, at least one of pi = border(pi + 1) and qi + 1 = border(qi) is true.
Instead of proving directly, we first introduce a way to compute all decompositions.
Let the longest palindromic prefix of S be a (a ≠ S), S = ax, longest palindromic suffix of S be b (it may be S), S = yb.
If x = b obviously S = ab is the only way to decompose.
If S = pq and p ≠ a, q ≠ b, p and q are palindromic, by Lemma 3 we have x, y are also palindromic.
So if neither x or y is palindromic, then S can't be composed to two palindromes.
If exactly one of x and y is palindromic, it's the only way to decompose S.
If both of them are palindromic, we can then find the second-longest non-self palindromic prefix of S: c. Let S = cz, if z is not palindromic or c = y, then S = ax = yb are the only non-strict palindromic decompositions. Otherwise, we can find all palindromic suffix of |S| whose lengths between |z| and |b|, their prefixes must also be palindromic (using Lemma 3 for ax and cz), then S = ax = cz = ... = yb (other palindromic suffixes and their corresponding prefixes are omitted)
Back to the proof of Lemma 7, the only case we need to prove now is S = ax = yb. Suppose the claim is incorrect, let p = border(a), s = border(y), S = ax = pq = rs = yb, (|a| > |p| > |y|, |a| > |r| > |y|, p and s are palindromic)
Continuing with the proof of Lemma 6, since t = 2, S = α2. If |p| ≥ |α|, 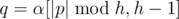 , so q would also be palindromic, contradiction. Therefore, |p| < |α| and similarly |s| < |α|. Let α = pq' = r's and the non-strict palindromic decomposition of α be α = βθ. Since α = pq' = βθ = r's, by Lemma 3 q' and r' should also be palindromic, contradiction.
, so q would also be palindromic, contradiction. Therefore, |p| < |α| and similarly |s| < |α|. Let α = pq' = r's and the non-strict palindromic decomposition of α be α = βθ. Since α = pq' = βθ = r's, by Lemma 3 q' and r' should also be palindromic, contradiction.
Lemmas are ready, let's start focusing on this problem. A naive idea is to count the number of palindromes in A and in B, and multiply them. This will obviously count a string many times. By Lemma 7, suppose S = xy, to reduce counting, we can check if using border(x) or border(y) to replace x or y can also achieve S. If any of them do, reduce the answer by 1, then we're done.
So for a palindromic string x in A, we want to count strings that are attainable from both x and border(x) and subtract from the answer. Finding x and border(x) themselves can be simply done by the palindromic tree.
Let x = border(x)w, we want to count Ts in B that T = wS and both T and S are palindromic. Since |w| is the shortest period of x, w can't be a power.
If |w| > |S|, w = S + U. S are U are both palindromes. Since w is not a power, it can be decomposed to be two palindromes in at most one way (Lemma 5). We can find that only way (by checking maximal palindromic suffix & prefix) and use hashing to check if it exists in B.
If |w| ≤ |S|, if S is not maximum palindromic suffix of T, w must be a power (Lemma 2), so we only need to check maximum palindromic suffixes (i.e. S = border(T)).
We need to do the similar thing to ys in B, then adding back both attainable from border(x) and border(y). Adding back can be done in a similar manner, or directly use hashing to find all matching w s.
Finding maximal palindromic suffix and prefix of substrings can be done by binary-lifting on two palindromic trees (one and one reversed). Let upi, j be the resulting node after jumping through fail links for 2j steps from node i. While querying maximal palindromic suffix for s[l, r], find the node corresponding to the maximal palindromic suffix of s[1, r] (this can be stored while building palindromic tree). If it fits into s[l, r] we're done. Otherwise, enumerate j from large to small and jump 2j steps (with the help of up) if the result node is still unable to fit into s[l, r], then jump one more step to get the result.
#include <bits/stdc++.h>
using namespace std;
const int N = 234567;
const int LOG = 18;
const int ALPHA = 26;
const int base = 2333;
const int md0 = 1e9 + 7;
const int md1 = 1e9 + 9;
struct hash_t {
int hash0, hash1;
hash_t(int hash0 = 0, int hash1 = 0):hash0(hash0), hash1(hash1) {
}
hash_t operator + (const int &x) const {
return hash_t((hash0 + x) % md0, (hash1 + x) % md1);
};
hash_t operator * (const int &x) const {
return hash_t((long long)hash0 * x % md0, (long long)hash1 * x % md1);
}
hash_t operator + (const hash_t &x) const {
return hash_t((hash0 + x.hash0) % md0, (hash1 + x.hash1) % md1);
};
hash_t operator - (const hash_t &x) const {
return hash_t((hash0 + md0 - x.hash0) % md0, (hash1 + md1 - x.hash1) % md1);
};
hash_t operator * (const hash_t &x) const {
return hash_t((long long)hash0 * x.hash0 % md0, (long long)hash1 * x.hash1 % md1);
}
long long get() {
return (long long)hash0 * md1 + hash1;
}
} ha[N], hb[N], power[N];
struct palindrome_tree_t {
int n, total, p[N], pos[N], value[N], parent[N], go[N][ALPHA], ancestor[LOG][N];
char s[N];
palindrome_tree_t() {
parent[0] = 1;
value[1] = -1;
total = 1;
p[0] = 1;
}
int extend(int p, int w, int n) {
while (s[n] != s[n - value[p] - 1]) {
p = parent[p];
}
if (!go[p][w]) {
int q = ++total, k = parent[p];
while (s[n] != s[n - value[k] - 1]) {
k = parent[k];
}
value[q] = value[p] + 2;
parent[q] = go[k][w];
go[p][w] = q;
pos[q] = n;
}
return go[p][w];
}
void init() {
for (int i = 1; i <= n; ++i) {
p[i] = extend(p[i - 1], s[i] - 'a', i);
}
for (int i = 0; i <= total; ++i) {
ancestor[0][i] = parent[i];
}
for (int i = 1; i < LOG; ++i) {
for (int j = 0; j <= total; ++j) {
ancestor[i][j] = ancestor[i - 1][ancestor[i - 1][j]];
}
}
}
int query(int r, int length) {
r = p[r];
if (value[r] <= length) {
return value[r];
}
for (int i = LOG - 1; ~i; --i) {
if (value[ancestor[i][r]] > length) {
r = ancestor[i][r];
}
}
return value[parent[r]];
}
bool check(int r, int length) {
r = p[r];
for (int i = LOG - 1; ~i; --i) {
if (value[ancestor[i][r]] >= length) {
r = ancestor[i][r];
}
}
return value[r] == length;
}
} A, B, RA, RB;
map<long long, int> fa, fb, ga, gb;
long long answer;
char a[N], b[N];
int n, m;
hash_t get_hash(hash_t *h, int l, int r) {
return h[r] - h[l - 1] * power[r - l + 1];
}
int main() {
#ifdef wxh010910
freopen("input.txt", "r", stdin);
#endif
scanf("%s %s", a + 1, b + 1);
n = strlen(a + 1);
m = strlen(b + 1);
A.n = RA.n = n;
B.n = RB.n = m;
for (int i = 1; i <= n; ++i) {
A.s[i] = RA.s[n - i + 1] = a[i];
ha[i] = ha[i - 1] * base + a[i];
}
for (int i = 1; i <= m; ++i) {
B.s[i] = RB.s[m - i + 1] = b[i];
hb[i] = hb[i - 1] * base + b[i];
}
power[0] = hash_t(1, 1);
for (int i = 1; i <= max(n, m); ++i) {
power[i] = power[i - 1] * base;
}
A.init();
B.init();
RA.init();
RB.init();
answer = (long long)(A.total - 1) * (B.total - 1);
for (int i = 2; i <= A.total; ++i) {
++fa[get_hash(ha, A.pos[i] - A.value[i] + 1, A.pos[i]).get()];
int p = A.parent[i];
if (p < 2) {
continue;
}
int l = A.pos[i] - (A.value[i] - A.value[p]) + 1, r = A.pos[i];
if (A.value[i] <= A.value[p] << 1) {
++ga[get_hash(ha, l, r).get()];
}
}
for (int i = 2; i <= B.total; ++i) {
++fb[get_hash(hb, B.pos[i] - B.value[i] + 1, B.pos[i]).get()];
int p = B.parent[i];
if (p < 2) {
continue;
}
int l = B.pos[i] - B.value[i] + 1, r = B.pos[i] - B.value[p];
if (B.value[i] <= B.value[p] << 1) {
++gb[get_hash(hb, l, r).get()];
}
}
for (int i = 2; i <= A.total; ++i) {
int p = A.parent[i];
if (p < 2) {
continue;
}
int l = A.pos[i] - (A.value[i] - A.value[p]) + 1, r = A.pos[i];
long long value = get_hash(ha, l, r).get();
if (gb.count(value)) {
answer -= gb[value];
}
int longest_palindrome_suffix = A.query(r, r - l + 1);
if (longest_palindrome_suffix == r - l + 1) {
continue;
}
if (RA.check(n - l + 1, r - l + 1 - longest_palindrome_suffix)) {
int length = r - l + 1 - longest_palindrome_suffix;
if (fb.count(get_hash(ha, l, l + length - 1).get()) && fb.count((get_hash(ha, l, r) * power[length] + get_hash(ha, l, l + length - 1)).get())) {
--answer;
}
continue;
}
int longest_palindrome_prefix = RA.query(n - l + 1, r - l + 1);
if (A.check(r, r - l + 1 - longest_palindrome_prefix)) {
int length = longest_palindrome_prefix;
if (fb.count(get_hash(ha, l, l + length - 1).get()) && fb.count((get_hash(ha, l, r) * power[length] + get_hash(ha, l, l + length - 1)).get())) {
--answer;
}
continue;
}
}
for (int i = 2; i <= B.total; ++i) {
int p = B.parent[i];
if (p < 2) {
continue;
}
int l = B.pos[i] - B.value[i] + 1, r = B.pos[i] - B.value[p];
long long value = get_hash(hb, l, r).get();
if (ga.count(value)) {
answer -= ga[value];
}
int longest_palindrome_suffix = B.query(r, r - l + 1);
if (longest_palindrome_suffix == r - l + 1) {
continue;
}
if (RB.check(m - l + 1, r - l + 1 - longest_palindrome_suffix)) {
int length = longest_palindrome_suffix;
if (fa.count(get_hash(hb, r - length + 1, r).get()) && fa.count((get_hash(hb, r - length + 1, r) * power[r - l + 1] + get_hash(hb, l, r)).get())) {
--answer;
}
continue;
}
int longest_palindrome_prefix = RB.query(m - l + 1, r - l + 1);
if (B.check(r, r - l + 1 - longest_palindrome_prefix)) {
int length = r - l + 1 - longest_palindrome_prefix;
if (fa.count(get_hash(hb, r - length + 1, r).get()) && fa.count((get_hash(hb, r - length + 1, r) * power[r - l + 1] + get_hash(hb, l, r)).get())) {
--answer;
}
continue;
}
}
for (int i = 2; i <= A.total; ++i) {
int p = A.parent[i];
if (p < 2) {
continue;
}
int l = A.pos[i] - (A.value[i] - A.value[p]) + 1, r = A.pos[i];
if (A.value[i] > A.value[p] << 1) {
++ga[get_hash(ha, l, r).get()];
}
}
for (int i = 2; i <= B.total; ++i) {
int p = B.parent[i];
if (p < 2) {
continue;
}
int l = B.pos[i] - B.value[i] + 1, r = B.pos[i] - B.value[p];
if (B.value[i] > B.value[p] << 1) {
++gb[get_hash(hb, l, r).get()];
}
}
for (auto p : ga) {
answer += (long long)p.second * gb[p.first];
}
printf("%lld\n", answer);
return 0;
}
Hope you enjoyed the round! See you next time!











Bonus for H: pick a as some non-empty substring of A and b as some non-empty substring of B. Concatenating them, he will get string ab. How many different palindromic strings can he get?
this one is easier
What I have so far:
It seems we are basically looking for string p and s such that ((AR contains s and B contains ps) or (AR contains ps and B contains s)) and p is palindromic (possibly empty). To prevent double counting AR should not contain xs or B should not contain xs, where x is the last character of p.
There are still some details to work out, but it feels like it should be possible to count these strings by creating a suffix tree containing AR and B to iterate over common substrings s, and by creating a palindromic tree to count the number of different p for each of them (by starting at the longest palindromes ending before the suffix leaves of the current node in the suffix tree and then calculating the number of ancestors of these nodes in the palindromic tree).
Is this also the approach you had in mind or am I overcomplicating things?
I think you approach is correct. There is also some approach using SAM or SA but I think there are many details whatever approach you use.
Excuse me? How can I find that problem ?
This is a problem used in Sichuan Team Selection Competition(for CNOI) 2017. I don't know anywhere to submit it:(
"and we didn't except anyone to pass."
should be *expect
Corrected, sorry about that.
What is the meaning of this line in Problem B :
"It's clear that the number of people having the same bi should be a multiple of bi".
and in Problem C i am not able to figure out how multiplying (m-1)with f[i-1][j-1] works please help me
Here is my editorial on Problem C. It may be helpful to you :)
And to explain the DP solution provided — f(i, j) is the number of ways of colouring i bricks with j bricks having a different colour to it's neighbour.
There are two options for the i-th brick.
Case 1 — It is the same colour as the (i — 1)th brick. In that case, f(i, j) += f(i — 1, j)
Case 2 — It is a different colour. Then the number of bricks with different colour increases from j to j + 1. And there are (m — 1) ways to colour this brick.
So, f(i, j + 1) += (m — 1)f(i — 1, j)
Thanks for helping i understand with the help of you answer
i don't understand how there are (m-1) way to colour this brick ? i mean there are j colour you used left side then you can use (M — j) colour we can select for f(n-1,k-1)
Brick #x should not have the same colour as Brick#(x — 1) and Brick#(x + 1).
It can have the same colour as Brick#(x — 2), Brick #(x — 3), etc.
ok, i understand thanks for helping
I also confused with the editorial so I'm writing this so anyone can help me to clear the idea.
let's say you have 10 people and the input:
10
7 7 7 7 7 7 8 8 9 9
person[0] = There are 7 people with different hat other than me
person[1] = There are 7 people with different hat other than me
person[2] = There are 7 people with different hat other than me
person[3] = There are 7 people with different hat other than me
person[4] = There are 7 people with different hat other than me
person[5] = There are 7 people with different hat other than me
person[6] = There are 8 people with different hat other than me
person[7] = There are 8 people with different hat other than me
person[8] = There are 9 people with different hat other than me
person[9] = There are 9 people with different hat other than me
Step:
Our current answer:
X X X X X X X X 1 1
(X = don't know yet, but can be assured that it's not 1)
Our current answer:
X X X X X X 2 2 1 1 (Observe that person 7 & 6 using different hat, not 1, not X)
Our current answer:
3 3 3 4 4 4 2 2 1 1
The editorial state that P must be divisible by Q because if it's not it'll add more difference than what's needed, (6/3 -> 3 Red 3 Blue, 2 different hats | 7/3 -> 3 Red 3 Blue 1 Green, 3 different hats) (CMIIW). It's not a mathematical proof but it's based on my intuition, I welcome any suggestions!
I have a doubt. If person[8] and person[9] have 9 people with different hats, shouldn't they have different hats.
X X X X X X X X 1 2
Please correct me if I am wrong. I didn't understand this part.
If they both have hat 1, won't there be only 8 people with different hats to them and not 9 ?
ghoshsai5000 is correct. Person[8] and person[9] should have different hats.
For problem B, considering a color of hats that b people are wearing, these b people will have this same b. Therefore, the people having this b must be a multiple of b (because every kind of such hats will contribute b such persons)
In problem D there is also a very simple solution with Dijkstra. We just have to find the maximum answer for 1 vertex and claim that it will be the same for everyone. Evidence: If from the first peak there is the worst way to some other one. Now let's iterate over everything except the other vertex. If one of them is better than the first one to this bad one, then why couldn’t we come first to this one, and then to the bad one? Then we will find a way shorter.__ My code:https://codeforces.com/contest/1081/submission/47122453
It's called prim.
Wow, I just realized that my E (47122728) isn't necessarily right (still got AC).
I just did greedy. At every even indexed position i, pick the smallest x such that the pref-sum[i+1] is a perfect square, and pref_sum[i] is a perfect square (assuming pref_sum[i] = x + pref_sum[i-1]).
To do this, we just keep one variable t, such that we put x = t^2 — sum[i-1] for the smallest t that works.
Now my mistake was thinking that all squares were at most 10^13, instead of all deltas being at most 10^13. If that holds, we can just keep trying t's until one works, since t never decreases in the algorithm, and when t^2 > 10^13, we can output FAIL. To check for working just binary search from a vector of squares or something.
Is there any input that hacks this?
For sure all squares are at most 1013. Let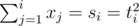 , because t2i2 - t2i - 12 ≤ t2i2 - (t2i - 1)2 = 2ti - 1 ≤ x2i, therefore t2i ≤ 105.
, because t2i2 - t2i - 12 ≤ t2i2 - (t2i - 1)2 = 2ti - 1 ≤ x2i, therefore t2i ≤ 105.
we didn't expect any to pass. That's too realistic.
hints are amazing!
sir,,,,problem (B) ,simple input and output same but wrong ans(WA) 1st case ans,Why do it?
https://codeforces.com/contest/1081/submission/47149223
You output 'possible'. It should be 'Possible', capital P.
Oh my god! Parity! How could I not have thought about it!
I have used the same approach but my answer is comming wrong . I have calculated (n-1)Ck*m*(m-1)^k, yet it is giving wrong ans with n=123, m= 45, k= 67. Here is link to my code Ideone.com.
Please tell me where I am wrong!!
Thanks in advance.
To divide a by b with modulo, you need to multiply a by reverse element of b under modulo m
https://codeforces.com/contest/1081/submission/47111844 see this submission
Can someone please explain problem B..?? i am having trouble understanding the language of the editorial, specially this line "It's clear that the number of people having the same bi should be a multiple of bi".
I've modified the editorial. Hope that helps.
in problem(D) does it matter whether we use prims or kruskal for making mst, my solution failing on test 18 ,lots of people failed on 18th please help me if you know something about that.
Try this: 3 2 2 1 2 1 2 1 2 3 47
bro it gives 1 1 which is right isn't . my code is https://codeforces.com/contest/1081/submission/47174196(kruskal) https://codeforces.com/contest/1081/submission/47170933(prims) after finding the mst i consider all the edges which have special vertex on both sides using recusion
You need build mst which contains all special vertex, but not for all tree. Edges with 1 and mb 0 special vertex can also be there. Test 18 checks that
thanks brother, i didn't use the technique described in editorial, problem was after obtaining the mst a method was required to consider all the edges which have special vertices on both sides(at any distance), i was leaving a case in that, now it is accepted:D
Can u please tell the insight behind using mst?
since there exist multiple paths between two vertices and the cost of EACH path is the maximum of all edges in individual path and the distance between two vertices is minimum of all path's cost. as for distance we are looking for minimum cost path for that purpose it is always good to select ONLY those set of vertices which are good enough to make the graph connected(tree) because from there if you add any more edge that will increase the number of paths between two vertices with heavier edges being introduced they(extra edges after mst) will never effect the distance between the vertices since their(extra edges) weight is more than previous ones(edges in the tree). so wee need to build a mst first and then find a way to account all the edges(having both side special tree) in the tree.
I don't understand how does the rfact[] work in Code2 of the Problems C. Can anyone tell me why we can do that instead of using divison. I have just learned programming for 2 months, so please don't laugh at me :)) Thanks for any helping
you can also find inverse like in this submission https://codeforces.com/contest/1081/submission/47111844. It uses euclidean theorem.....google it.
Can anyone explain D..specifically why mst is being used and where do we get the intuition to use it in this problem?
In D we can just binary search on answer. For fixed
costwe can run bfs from any special vertex on graphG'whereG'is exactly the same graph but with removed(disabled) edges withedge_cost > costand check whether we can visit every special vertex. It's possible to check this condition by running bfs from any special vertex onG'.In this binary search we have to find the smallest possible value that satisfies the condition above.
literally how I solved it. Beautiful solution.
We can also solve it with union-find algorithm instead of bfs.
What am I missing in my code for problem D? WA on TC 7. Plz Help. https://codeforces.com/contest/1081/submission/47271236
I am getting TLE for the code (47303815). I have used Kruskal along with disjoint set. Link to code: https://codeforces.com/contest/1081/submission/47303815
use & for a vector parameter, but anyway your solution was incorrect
Yes I used the & operator, let me check what is the error. Thank you linjek
Can anyone explain me how this code from C calculates the number of combinations to take k from n-1?
I didn't understand the second solution for problem C. I understood we are taking all the possible combinations for the k bricks which satisfy the condition. Then I didn't understand that how the term m * (m — 1) ^ k is handling all the possible cases.
These k bricks must be taking a color different from its left neighbor, so each of them has $$$m-1$$$ ways of choosing their colors. Also we have $$$m$$$ colors for the first brick.
Thanks. I got it now
A lot of fun, i solved problem C by the mix of 2 solutions that editorial promoted.
Check my submission
could someone please explain question C Problem C I am confused with the statement . Please help Thanks and regards
There must be exactly K bricks whose color differs from its left neighbour.
Eg: RR B BB G GG .In this case K will be 2
anyone explain the implementation of D not able to understand